数学最強キャラ考察スレ 考えられる限りの、最大に巨大な物体を作る。(8/10)
レベル7 コンパクト基数
それでは可測基数より大きな存在はあるか?
→ あります。
しかも比較的簡単に見つかります。
可測基数Tの定義は
「可測基数Tはピラミッド型。αの横と縦を全て網羅している」
です。
Tは物知りさんですけど、
ただしαに関する情報しか知りません。
お隣にあるβ、
もしくはβピラミッドの事は何も知りません。
ここに可測基数を拡大する余地があります。
そこで次のレベル。
コンパクト基数が登場します。
コンパクト基数Cとは
「世の中に存在する全ての基数γ(γの大きさはCよりも大きい事もある)の成分を十分多数含んでいて、
必要ならばメンバーをかき集めてγを復元する事ができる」
ほどの大きさを持つ基数の事を言います。
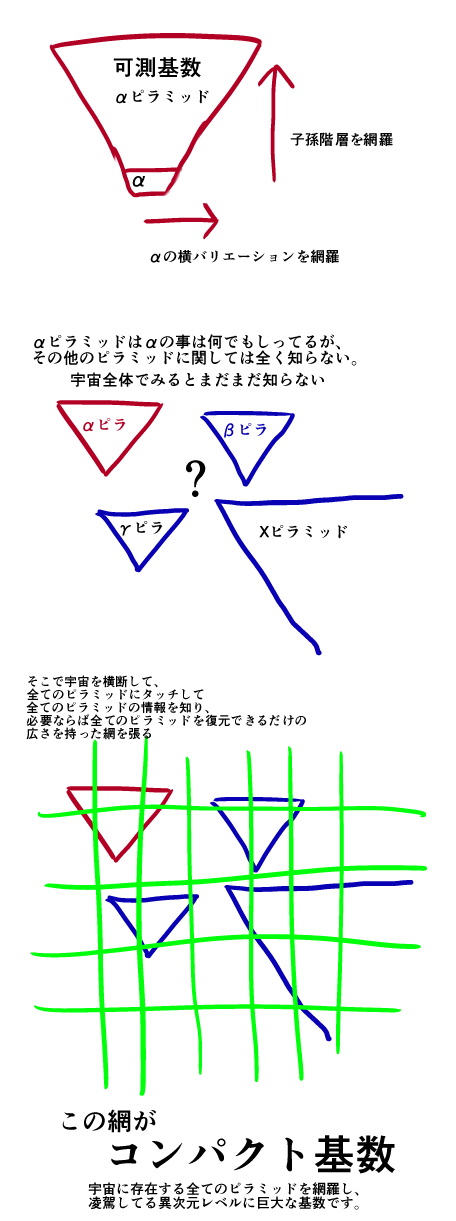
つまり
可測基数が
とてつもなく巨大な、しかし単一のピラミッドだとしたら、
コンパクト基数は宇宙に存在する
全ての到達不能基数ピラミッドに
ちょっとづつタッチして、
宇宙全域の情報をしっている
ウェブ型の形をしています。
当然サイズとしては
コンパクト基数 >>>>>> 可測基数
となります。
実際デカい。
可測基数が一個の原子だとしたら、
コンパクト基数は宇宙全体の原子の数ぐらいに
大きさが違う。
さて、ここで一つの疑問としては
「いやアンタ。そんなに巨大な基数が欲しいなら、手っ取り早く『基数Xは、他の全ての基数Yを含む』と定義してしまえばいいんじゃ?」
と思うかも知れませんが、それはダメなんです。
なぜなら
「基数Xは全ての基数Yを含む」
と言ってしまうと、
「基数Xは基数Xを含む」
事になり、
X > X
で、矛盾が発生する。その言い方じゃダメなんです。
だからわざわざ「コンパクト基数Cは 他の基数γの部分成分を含み、γを復元できる」
みたいな、部分的にだけタッチし
そこから全体を復元できる、みたいな
捻った定義になっているわけなんですね。
ちゃんと考えられてるんですよ。^^;
前ページ 次ページ
1 2 3 4 5 6 7 8 9 10
トップへ
