数学最強キャラ考察スレ 考えられる限りの、最大に巨大な物体を作る。(7/10)
それでは到達不能基数よりも大きな物体を考えましょう。
レベル6 可測基数
正式な用語ではない私の創作ですが、
仮に「到達不能基数より大きな基数」を便宜上「アウター基数」とでも呼びましょう。
「アウター基数」に必要な条件を調べます。
そもそも基数の上下関係とは
X < 2X
が基本。
(対角線論法で証明できる。これはどんなXでも成立する。)
Xは自分の子供、2Xの全メンバーを把握しきれない。
親(X)は子供(2X)の事で知らない事がある
と言うのが根本の原理にあります。
そこで発想の逆転。
「アウター基数Tは、自分の子要素、孫要素、ひ孫要素、・・・をTの中に含んでいる」
と、最初から定義の中に入れてしまいます。
つまりアウター基数Tを作る時は
セルフピラミッド。
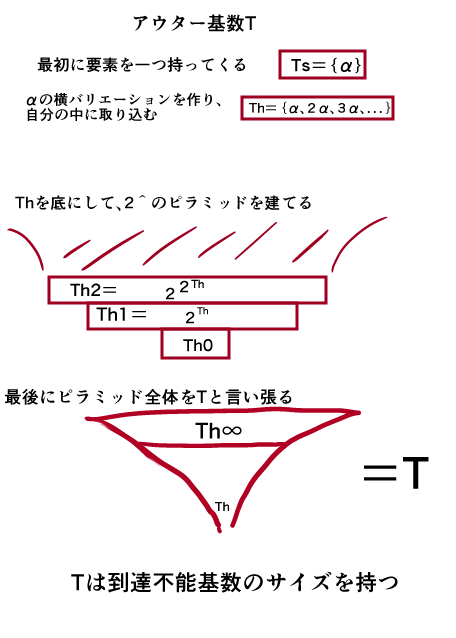
まず最初に適当なシングル要素αを入れ、
次にαを加法で増殖させるだけ増殖させて横に増やし、
、
次に2Tをして子を作り、
次に22Tをして孫を作り、
次に222Tしてひ孫を作り、
縦に伸ばして、
ピラミッドを作り、
最後に「このピラミッド全体がアウター基数Tを構成する」と
宣言します。
はい、こうして出来たのが可測基数です。
(アウター基数は到達不能基数を超える為に必要な条件。
その具体例が可測基数)
可測基数は(定義により)「『全て世代の子要素』を知っている」ので
Tはω∞個数を持っています。
よって
可測基数 ≧ 到達不能基数
到達不能基数についに到達しました。
なお可測基数の存在は
通常の数学からは証明不可能です。
つまり可測基数のピラミッドはデカいですが、
これを構築するには
∞回の操作が必要になる。
定義としては示せても、
人間が実際に構築するのは不可能。(^_^;
よって可測基数の存在を認める為には
「可測基数は存在する」と言う
新しい公理を導入して、
無理矢理に作ってしまいます。それしか方法がない。
→ まあそこが問題。
新しい公理(ルール)を導入したら
それはもはや別のゲーム。
数学と呼べるかどうかも正直微妙。
オレ(大多数の数学者)知らないから、あとはおまえたち勝手にやってろって感じ。^_^A;
・・・うーん、でもまあ。面白けばいっか。(爆)
構わず次行きましょう。
前ページ 次ページ
1 2 3 4 5 6 7 8 9 10
トップへ
