数学最強キャラ考察スレ 考えられる限りの、最大に巨大な物体を作る。(5/10)
レベル4 ωn階層 無限大
はい、それではω1より巨大な物体はあるか?
あります。
答えは意外と簡単。
2ω1です。
すなわちさっき出てきたω1メンバー全てにON/OFFスイッチを設置し、
| 2ω1のメンバー | スイッチ
|
| {} | 
|
| {1} | 
|
| {2} | 
|
| {1,2} | 
|
| {3} | 
|
| {1,3} | 
|
| {2,3} | 
|
| {1,2,3} | 
|
| {4} | 
|
| {1,4} | 
|
| {2,4} | 
|
| {1,2,4} | 
|
| {3,4} | 
|
| {1,3,4} | 
|
| {2,3,4} | 
|
| {1,2,3,4} | 
|
| {5} | 
|
| ・・・ | 
|
→ { {},{1},{1,2},{1,2,3},{4},{2,4},{1,3,4},{2,3,4},{5},...
ONになってる要素を抜き出して、集める。これが1要素になる。
そしてそのスイッチパチパチを、
全ての組み合わせで試し、
出てくる全ての要素をコレクションしたのが
=2ω1
です。
対角線論法により
2ω1のサイズ > ω1のサイズ
が証明されます。
新しい無限が出てきたので
2ω1 = ω2
と呼びましょう。
えーっと、この辺りで数学用語「基数」が出てきます。(´д`;
簡単に言うと
基数=構造
の事です。
(正確には構造をisomorphicで割って、同一構造のラベル違いを一本化した物。それが基数。)
なぜ基数なんてワードが出てくるかと言うと
ω0=自然数のサイズと同じ
ω1=実数のサイズと同じ
ω2=「数」での相当例なし
ω2からは、数での相当例がない。
数のサイズを超える世界に入ったので
そこで基数=巨大な構造物として捉えます。
さてこんな議論を繰り返すと
ω3 = 2ω2 > ω2
ω4 = 2ω3 > ω3
ω5 = 2ω4 > ω4
・・・
こーんな感じで
ω0 < ω1 < ω2 < ω3 <・・・
でチェーンが延々と伸びてゆきます。
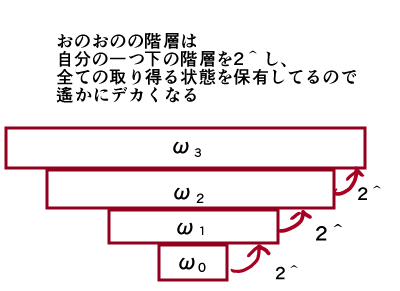
さてチェーンはどこまで伸びてゆけるでしょうか?
限界があります。
それが「到達不能基数」です。
前ページ 次ページ
1 2 3 4 5 6 7 8 9 10
トップへ




































