数学最強キャラ考察スレ　考えられる限りの、最大に巨大な物体を作る。(4/10)


レベル3　実数無限大：ω1


無限と言えばデカい数ですから、
それよりも上なんてあるのか？
と思うかも知れませんが。

いや案外あります。


カントールが1900年頃に
2∞　＞　∞
と言う原理を発見し、
無限にも大きさのランクがある事が知られました。


私も以前のコラム無限にも大きさのランクがあるで紹介しました。


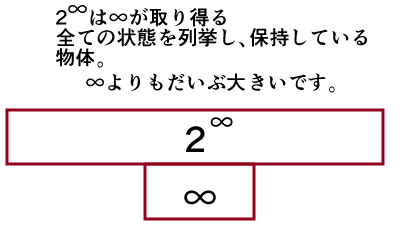
この2∞とはどんな形かと紹介すると、

∞が全ての自然数をコレクションした物。つまり
　∞ = {1,2,3,4,5,・・・・}
とすると

次に∞の全ての要素に対してON/OFFスイッチを設置し、

1　
2　
3　
4　
・・・

こいつらを適当にパチパチして、
ONが点灯してる要素を取り出して
一つの列を作ります。

例：
1　
2　
3　
4　
・・・
→　{1,3,4,・・・}

そしてこのパチパチを、
全ての組み合わせで試し、
結果を全てコレクションします。
（だからオン/オフの2つの組み合わせを、ωに無限個並べるから2ωって形になる）


具体的には
2ω　＝
{
}
のような形になります。
これが2∞です。

対角線論法により
　2∞のサイズ　＞　∞のサイズ
が証明されます。





さて無限が二つ出て来てしまった為に
今後は両者を区別するために
　 整数無限大 ＝ ∞ ＝ ω ＝ ω0
　2^ω ＝ 実数無限大＝　ω1
と言う言葉を使います。


それでは、
ω1を超える巨大なサイズの物体はあるか？
　→　あります。

前ページ　次ページ

1 2 3 4 5 6 7 8 9 10

トップへ