

| 年 | 出来事 | 所感 |
| 2010年04月 | ジュエルペットてぃんくる☆ 放送開始 | |
| 2010年11月 | 第33話「夢に向かってドッキ☆ドキ!」 | 2010年11年15日の日記 この時点で「10年に1本の大傑作になる」と自分の日記に書いてました。 |
| 2011年04月 | 放送終了 | 2011年04月02日の日記 感動しまくり。最終回に衝撃受けてペットロスを経験したような状態になる。 |
| 2011年07月 | DVD-BOX発売 | 2011年07月23日の日記 DVD-BOXレビュー |
| 2011年09月 | ファンディスク発売 | 2011年09月14日の日記 FD1レビュー |
| 2012年01月 | ファンディスク2発売 | 2012年01月17日の日記 FD2レビュー |
| 2012年09月 | 公式でBD-BOX&OVA化プロジェクト発足。出資を募る。 | 2012年09月06日の日記 参加表明 |
| 2012年09月 | ファンディスク3発売 | 2012年09月11日の日記 FD3レビュー |
| 2012年11月 | プロジェクト成功。OVA製作開始。 | 2012年10月21日の日記 やったね |
| 2013年07月 | BD-BOX & 新作OVA | 2013年07月22日の日記 BD-BOXレビュー |







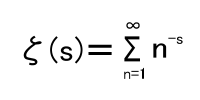

|








 35分切れました。
35分切れました。