よくわかるカオスとフラクタル。数学的解法の限界5(2010/01/01)

カオス図:
今までの結果をまとめて振り返ってみましょう。
c=0.50 → y=0.000
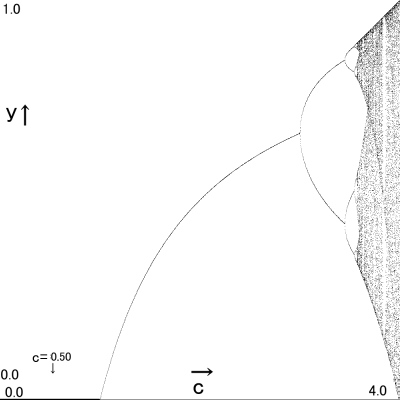 「簡単じゃん」
「簡単じゃん」
c=1.57 → y=0.333
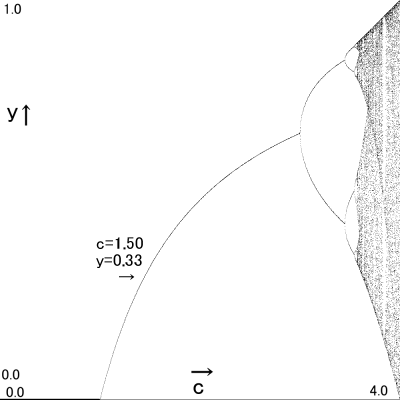 「まだわかる」
「まだわかる」
c=3.47 → y=0.45、0.84
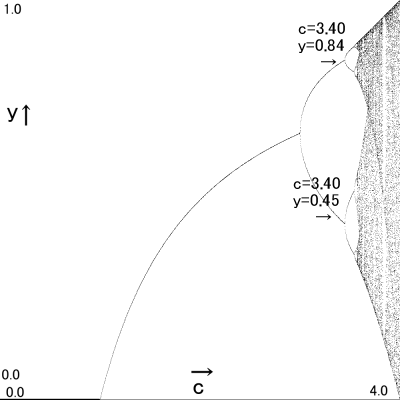 「2つに収束するようだ」
「2つに収束するようだ」
c=3.47 → y=0.395、0.832、0.487、0.869
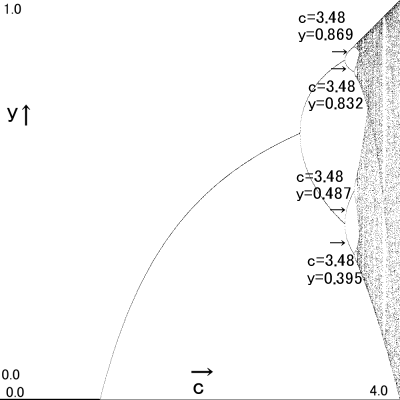 「4つか。まだなんとか。」
「4つか。まだなんとか。」
c=3.67 → y=・・・・・
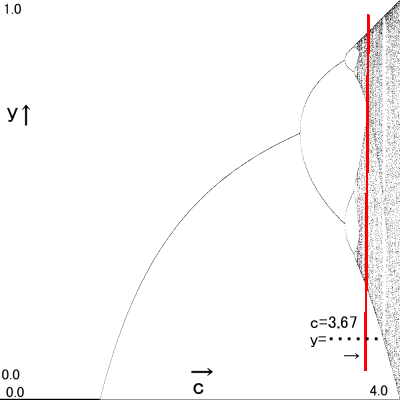 「急激に何億、何兆の分岐へ。動きが不規則すぎてこれ以上は予測できない。」
「急激に何億、何兆の分岐へ。動きが不規則すぎてこれ以上は予測できない。」
c=3.83 → y=0.156、0.505、0.957
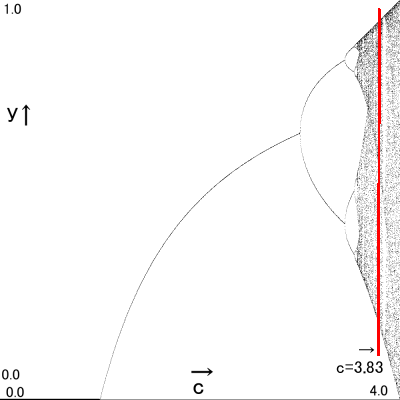 「えっ、ここは3つでいいの!?」
「えっ、ここは3つでいいの!?」
c=3.87 → y=・・・・・
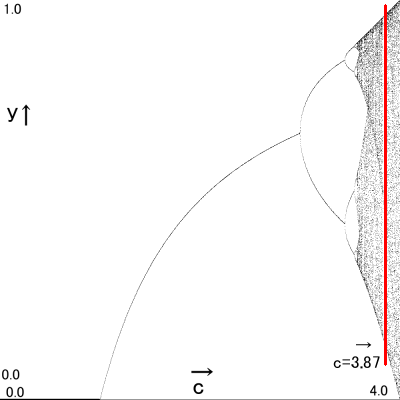 「またかよ。無理。絶対無理。」
「またかよ。無理。絶対無理。」
このような、
最初は単純に見えてるのに
ある時から急に恐ろしく複雑、予測不可能な事態に変形する現象を一般に「カオス」と呼びます。
しかもこの複雑極まりない現象を産み出した計算式は基本的に
xn+1= c・xn・(1-xn)
ただ一つと言う単純さ。(冒頭の式と実質同じ。違う表記法をしているです。)
たったこれだけの式から

形容しがたい奇妙な図形が出てきます。
まあカラクリはどこにあるかと言うと、式を再帰的に無限回繰り返して増幅したからなんですが。
だって展開したら
- x0= u として
- x1= c・u・(1-u)
- x2= c・x1・(1-x1)
= c・c・u・(1-u)・(1-c・u・(1-u))
- x3= c・x2・(1-x2)
= c・c・c・u・(1-u)・(1-c・u・(1-u))・(1-c・c・u・(1-u)・(1-c・u・(1-u)))
- x4= c・x3・(1-x3)
= c・c・c・c・u・(1-u)・(1-c・u・(1-u))・(1-c・c・u・(1-u)・(1-c・u・(1-u)))・(1-c・c・c・u・(1-u)・(1-c・u・(1-u))・(1-c・c・u・(1-u)・(1-c・u・(1-u))))
- x5=・・・・
な無限項の多項式になるんですからそりゃ複雑になりますって(^^A;
問題の複雑さは人知の限界を超え
例えば
「c=3.600の時に、yの収束点はいくつに分岐するか。
また各収束点の値を求めて述べよ。」
などのような問題が出された時には完璧に解答不能です。
例えこのあと何万年の数学の発達を待ったとしてもこの問題を
効率的に解く方法は発見されないでしょう。
解答する方法は唯一、
コンピューターに計算式をぶち込んで
何億回も計算させてシミュレートさせ
どうなったか出てきた答えを見るだけ。
他に方法はありません。
カオスはコンピューターの発明で初めて発見された現象ですねー。
決して数学では答えの出せない問題。
数学も万能ではありません。
数学者には解けない、すなわち
「問題を簡素化し、より短時間で解く有効な解法」が存在しないような問題も知られています。
有名な所では例えばP≠NP問題でしょうか。
「巡回セールスマン問題」に代表されます。
P=Polynomialは多項式。すなわち問題のパラメーターの個数nに対して固定されたm、そしてnmの計算コストがかかる問題。
NP=NonPolynomialは一般的にはn!(=1×2×3×・・・×n)。問題のパラメーターの個数nに対してnnの計算コストがかかる問題です。
後者の方が計算量は爆発的に増加します。
例えば最適ルートの95%以内の時間を保証するルート、または95%の確率で最適ルートに合致する、
などの条件を落としたルートをP級の短時間で見つける解法は見つかっていますが
今もって本当の最適ルートを見つけるには
コンピューターを使って全てのn!ルート、および各所有時間を直接計算し
総当たり(NP級の計算量)で見てみる以外に解法はないとされています。
(明らかに失敗するルートなどで可能性を絞れば当然n!全てを見る必要はありませんが、計算コストは依然n!級には変わりありません。)
P≠NP問題は誰一人証明を見つけていない数学界難題の一つですが
まずほとんど100%の数学者はP≠NPを予想しています。
すなわち「コンピューターでも使って総当たりで計算する以外の解法は存在しないだろう」と。
カオスも似たような物ですね。
「c=3.600の時に、yの収束点はいくつに分岐するか。
また各収束点の値を求めて述べよ。」
このような問題はコンピューターを使ってひたすら計算して総当たりに解く以外の方法は恐らく存在しないでしょう。
なにしろ実際にコンピューターが無限回近くの計算を行って作られた人工的なモデル。
有限の長さの式しか扱えない数学者では勝てません。ノートに書くには余白が少なすぎる。
まあ、そういうわけでカオス現象が発見された当時は数学界も新しいジャンルの誕生か?とにわか色めき立った物ですが
数学では扱いようのないタイプの問題だと判明した今では
どちらかと言うとコンピューター屋、または科学の部門にお任せ。
数学ではないとするのが一般的ですね。
世の中には数学では解けない問題もあるんです。あしからず・・・(汗)
なお例のグラフの先はc=4.00からどうなっているか疑問に持つ方もおられると思うので
追記しておきますがc=4.00以上はyの値0.00〜1.00の範囲を超えて無限大に発散するので
どこにも収束せずグラフは描けません。
無理矢理やるとこうなります。
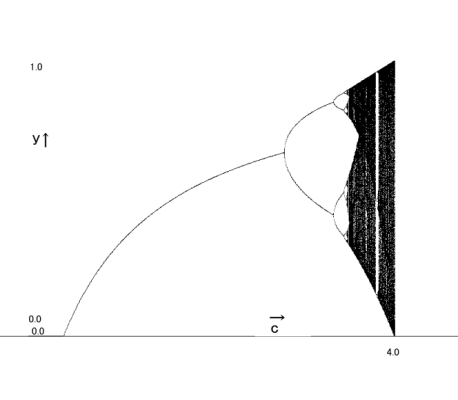 シュールだ。(笑)
シュールだ。(笑)
そして最後に8000x8000の特大カオス画像を置いておきます。
.bmpで62.5M相当の巨大な画像なのでメモリが許すなら解凍してからご覧ください。

chaos8000.zip ダウンロード
次章ではフラクタルを見てみます。
カオスと同じくコンピューターの発達で発見された現象。フラクタルとはいったい何なのでしょうか。
第1章へ 前章へ 次章へ 第7章へ
最新の日記へ


 「簡単じゃん」
「簡単じゃん」 「まだわかる」
「まだわかる」 「2つに収束するようだ」
「2つに収束するようだ」 「4つか。まだなんとか。」
「4つか。まだなんとか。」 「急激に何億、何兆の分岐へ。動きが不規則すぎてこれ以上は予測できない。」
「急激に何億、何兆の分岐へ。動きが不規則すぎてこれ以上は予測できない。」 「えっ、ここは3つでいいの!?」
「えっ、ここは3つでいいの!?」 「またかよ。無理。絶対無理。」
「またかよ。無理。絶対無理。」
 シュールだ。(笑)
シュールだ。(笑)