よくわかるカオスとフラクタル。数学的解法の限界6(2010/01/01)
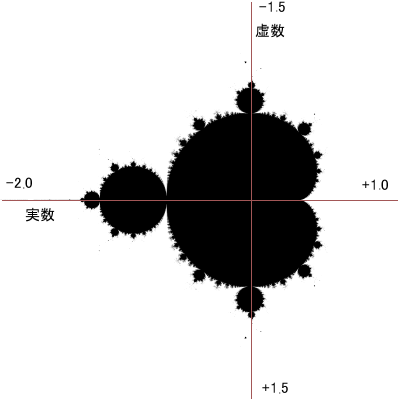
フラクタルで有名と言えば上記の画像でしょう。
(色がついてるのは後から作られたモデル。白黒2値にきっちり分かれてるのは脚色の入ってない本家図。)
発見者の名にちなみ「マンデルブロー集合」と呼ばれます。
形がどことなく虫っぽく見えるので比喩でマンデルブロー虫とも呼ばれますね。(^^;
まあまずはYouTubeのこの動画をご覧ください。
マンデルブロー虫の一部を拡大してゆくと
マンデルブロー虫の中に新しいマンデルブロー虫が。
そして新しいマンデルブロー虫の一部を拡大してゆくとその中にまだマンデルブロー虫が。
これがフラクタルの世界。
なおマンデルブロー図が有名になりすぎたためフラクタル=マンデルブローと混同されがちですが
フラクタルとは「自己相似」の意味です。
「自己相似」な性質を持つ図形は全てフラクタルであり、
マンデルブロー集合はフラクタル性質を持つ図形の特定の一種です。
他にもジュリア集合などがフラクタルの例として挙げられます。
この不思議な図形がどうやって描かれたのか次章で具体的に計算してゆきます。
第1章へ 前章へ 次章へ 第7章へ
最新の日記へ
