よくわかるカオスとフラクタル。数学的解法の限界4(2010/01/01)

カオス図:
この調子で計算してゆくとc=3.565ぐらいの時は収束値は8個=線も8本に分岐します。
そしていよいよカオスが始まる。
c=3.67だと
収束値は y= 0.591 → 0.887 → 0.367 → 0.853 → 0.460 → 0.912 → 0.295 → 0.764 → ・・・・(一例)
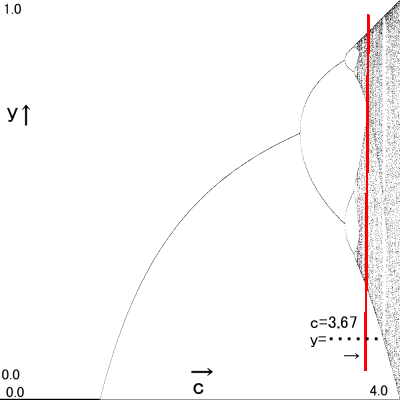
いや、もう収束なんて呼べない。
ほぼ永遠に変化し続け収束はしません。
グラフもこれら全ての数字に対応した場所に点が打たれ
すさまじい超分岐に。
収束値がどう動くのかは誰にも全く予想できない
とんでもなく複雑な力学系になってしまいました。
しかし、このまま予想のつかない超分岐が続くかと思えば
ところがどっこい!
c=3.83の所を見ると
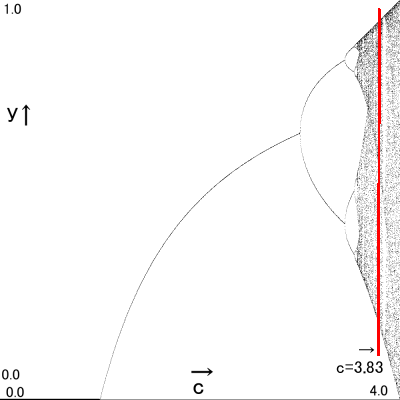
なんか隙間があるように見えます・・・・
そう、実際c=3.830の場所では
y= 0.156150 → 0.504667 → 0.957417 → 0.156150 → ・・・・
の3パターンループに突入し暴風雨はいきなり止んでます。
えっ、カオス終焉?
ですがc=3.87になるとまた
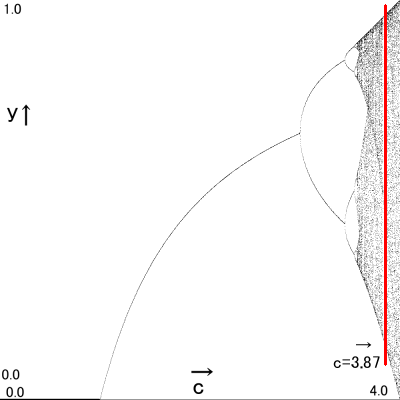
y= 0.881653 → 0.403800 → 0.931686 → 0.246316 → 0.718445 → 0.782831 → 0.657925 → ・・・・(一例)
の超分岐に突入。
超分岐に入ったと思ったら
ある時パタっと急に収まってまた超分岐に入る。
まさにカオス。挙動に予測がつかなすぎる。
第1章へ 前章へ 次章へ 第7章へ
最新の日記へ



