よくわかるカオスとフラクタル。数学的解法の限界1(2010/01/01)

まずはこの図をご覧ください。
これが今じゃ有名な「カオス」と呼ばれる現象の発端になった一枚の画像です。
仮に横軸をc,縦軸をyと読んで数値をつけるとこんな感じになるのですが
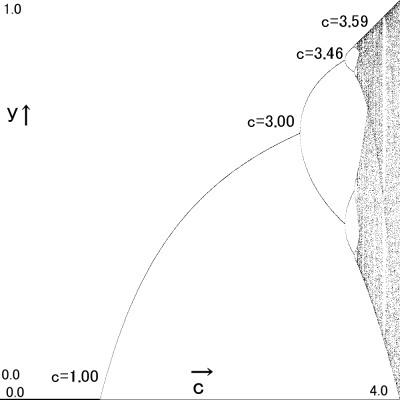
c=0.00〜1.00の間まではy=0.00で地面を張ってるのですが
c=1.00からカーブを描いて上に上がり、
c=3.00の時点で2本に分岐。
c=3.46ぐらいの時点で4本に分岐。
それからも分岐を繰り返しc=3.59の時点ではもう手のつけようがないほど分裂して
恐ろしい事に。
この奇妙なグラフ(?)
いったいどうやって描かれたのでしょうか。
説明したいと思います。
式は
y(c,x,0) = x
y(c,x,n+1)= c・y(c,x,n)・(1-y(c,x,n))
y(c) = y(c,x,∞)
c=0.00〜4.00、x=0.00〜1.00の範囲を動くとする。
こんな感じです。
一つのyにつきc,x,nの三つのパラメーターがある三重式です。
そして固定されたcにつき、xを0.0〜1.0の範囲、nを0〜∞までの整数範囲で動かし
全ての組み合わせでy = y(c,x,∞)を算出し
その結果をグラフ上に打った物です。
いや、もう具体的に示しましょう。(^^;
次ページをご覧ください。
第1章へ 次章へ 第7章へ
最新の日記へ

