よくわかるカオスとフラクタル。数学的解法の限界7(2010/01/01)
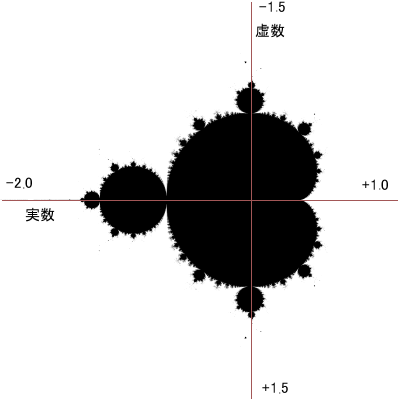
マンデルブロー図は複素数c(実数+虚数)の式で定義されます。
f(c,0) = 0
f(c,n+1)= f(c,n)2+c
f(c) = f(c,∞)
f(c)が発散する点では白く、発散しない点では黒く塗る。
この図ではc=実数(-2.00〜+1.00)、虚数(-1.50〜+1.50)の範囲で描画。
別の書き方をすればzn+1= zn2+c (z∞が発散すれば白、発散しなければ黒。)
おや?
どことなくカオスの式
y(c,x,0) = x
y(c,x,n+1)= c・y(c,x,n)・(1-y(c,x,n))
y(c) = y(c,x,∞)
別の書き方でxn+1= c・xn・(1-xn)
と似てますね。
どちらもコンピューターを使いxn+1=f(xn)
と言う形の再帰演算を果てしなく繰り返した結果に発見された現象なので
まあ必然だったのでしょう。
ではまた「わかりやすく」具体的に数値を入れながらどうやって図が描かれたのか計算してみましょう。
レッツゴー。
例えば座標(0.3、0.5)を見てみましょう。
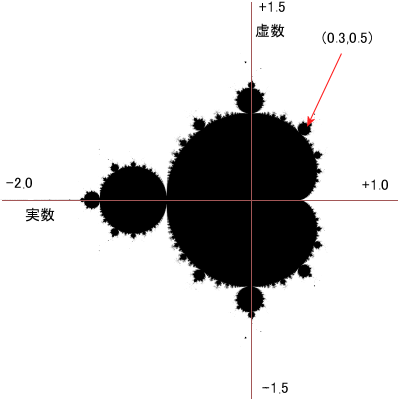
図で見るとこの位置は黒くなってますねー。
なぜ黒いのか計算して示します。
- 座標(0.3、0.5)を複素数cに変換。
c=0.300 + 0.500i (iは虚数)
- まずf(c,0) = 0
よってf(c,0)=0.000 + 0.000i;
- 次にf(c,n+1)= f(c,n)2+c
f(c,1)= f(c,0)2+c
= (0.000 + 0.000i)2+0.300 + 0.500i
= 0.300 + 0.500i
-
f(c,2)= f(c,1)2+c
= (0.300 + 0.500i)2+0.300 + 0.500i
= 0.140 + 0.800i
-
f(c,3)= f(c,2)2+c
= (0.140 + 0.800i)2+0.300 + 0.500i
= -0.320 + 0.724i
-
f(c,4)= f(c,3)2+c
= (-0.320 + 0.724i)2+0.300 + 0.500i
= -0.122 + 0.036i
- f(c,5)= +0.313 +0.491i
- f(c,6)= +0.157 + 0.808i
- f(c,7)= -0.328 + 0.754i
- f(c,8)= -0.160 + 0.005i
- f(c,9)= +0.326 + 0.498i
- f(c,10)= +0.158 + 0.825i
- f(c,11)= -0.355 + 0.760i
- ・・・・
どうやらx=-1.0〜+1.0、y=-1.0〜+1.0の間をフラフラ彷徨ってるようです。
この後は何万回計算を続けてもfは無限大に発散しないので座標(0.3、0.5)は黒く塗りつぶします。
次にちょっとお隣の座標(0.4、0.5)を見てみましょう。
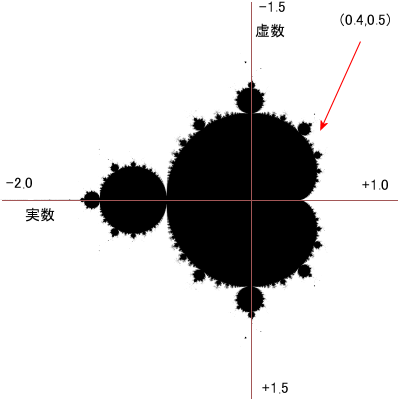
比較的近い点同士なのにこちらは白くなってますね。
なぜ白いのか計算して示します。
- 座標(0.4、0.5)を複素数cに変換します。
c=0.400 + 0.500i (iは虚数)
- まずf(c,0) = 0
よってf(c,0)=0.000 + 0.000i;
- 次にf(c,n+1)= f(c,n)2+c
f(c,1)= f(c,0)2+c
= (0.000 + 0.000i)2+0.400 + 0.500i
= 0.400 + 0.500i
-
f(c,2)= f(c,1)2+c
= (0.400 + 0.500i)2+0.400 + 0.500i
= 0.310 + 0.900i
-
f(c,3)= f(c,2)2+c
= (0.310 + 0.900i)2+0.400 + 0.500i
= -0.314 + 1.058i
- f(c,4)= -0.621 - 0.164i
- f(c,5)= +0.758 + 0.704i
- f(c,6)= +0.480 + 1.568i
- f(c,7)= -1.828 + 2.004i
- f(c,8)= -0.277 - 6.827i
- f(c,9)= -46.13 + 4.287i
- f(c,10)= +2109.9 - 395.0i
- f(c,11)= +4295642.7 - 1666719.8i
- ・・・・
ありゃー、ぶっ飛んじゃいました。
この後は数値はどんどん大きくなり止まらず無限大に発散します。
よって座標(0.4、0.5)は白く塗りつぶします。
このようにして全てのc=x+yi点で
f(c,0) = 0
f(c,n+1)= f(c,n)2+c
f(c) = f(c,∞)
を計算しf(c)が無限大へ発散するなら白、しないなら黒で塗りつぶして
マンデルブロー図は完成します。
色がついてるモデルは発散・収束まで要した回数の大小などの要素によって色を塗り分けた物で
明るい/暗い所ほど発散が早い/遅いに対応してます。
(本質的には本家の白黒と全く同じです。)
いかがでしたでしょうかフラクタル。
これもカオスと同じくコンピューターを使って初めて見れるようになったとてもとても奇妙な図形。
数学的な観点から見ると
フラクタルはカオス同様コンピューターを使って無理矢理解くしかないので大変扱いにくく、^^;
また数学的にもあまり興味を引く問題もないので
どちらかと言うとコンピューター・科学系のジャンルに分類されると個人的には思います。
しかしグラフィック的には大変面白く
数式から発生したこんな不思議な図形が存在する事の発見は
人類の文化的に興味深い出来事の1ページだったと思います。
フラクタル図形に延々とズームしてゆく気が遠くなるムービーです。
左下に出てる10nのnは1の後に0がn個続く意味です。
例:1020=100000000000000000000倍ズーム
ズームは永遠に終わりません。
いくら拡大しても図形はそれ以上の細かい模様で描かれていて次々と新しい詳細が出てきます。
お付き合いありがとうございました。
第1章へ 前章へ 第7章へ
最新の日記へ


