よくわかるカオスとフラクタル。数学的解法の限界3（2010/01/01)
カオス図：
面白いのはcが3.00を超えた後です。
グラフで見ると線が分岐してますね。
これは値の収束値が二つ以上ある事を意味します。
どういう意味なのか具体的に計算して示します。
c=3.40を取りましょう。
グラフでの対応値はy=0.45とy=0.84。
これらがどうして出てきたかまた具体的に計算します。
- 1．まずはc=3.4と取る。
- 2A．初期値x=0.0は答えが0になるので無視する。
- 2B．次に初期値x=0.1と取る。
- 3A
y(c,x,0) = x
よって
y(3.4,0.1,0) = 0.1
- 3B
y(3.4,0.1,1)= c・y(3.4,0.1,0)・(1-y(3.4,0.1,0))
y(3.4,0.1,1)= 3.4・0.1・(1-0.1)
y(3.4,0.1,1)= 0.306
- 3C
y(3.4,0.1,2)= 3.4・0.306・(1-0.306)
y(3.4,0.1,2)= 0.722
- 3D
y(3.4,0.1,3)= 3.4・0.722・(1-0.722)
y(3.4,0.1,3)= 0.682
- 3E
y(3.4,0.1,4)= 3.4・0.682・(1-0.682)
y(3.4,0.1,4)= 0.737
- 3F
y(3.4,0.1,5)= 3.4・0.737・(1-0.737)
y(3.4,0.1,5)= 0.659
- ・・・・・
- y(3.4,0.1,36)= 0.452
- y(3.4,0.1,37)= 0.842
- y(3.4,0.1,38)= 0.452
- y(3.4,0.1,39)= 0.842
- y(3.4,0.1,40)= 0.452
- y(3.4,0.1,41)= 0.842
- ・・・・・・・
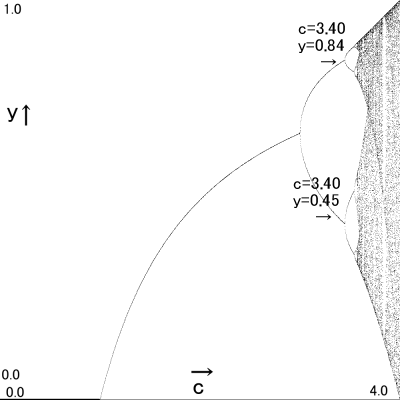
- どうやら0.452と0.842を繰り返してるようです。
よってグラフのc=3.4についてはy=0.452の位置とy=0.842の両方の位置に点を打つ。
- 2C．次に初期値x=0.2と取る。
- 同様の手順で
y(3.4,0.2,0) = 0.544
y(3.4,0.2,1) = 0.843
y(3.4,0.2,2) = 0.449
y(3.4,0.2,3) = 0.841
y(3.4,0.2,4) = 0.454
y(3.4,0.2,5) = 0.843
y(3.4,0.2,6) = 0.450
y(3.4,0.2,7) = 0.843
y(3.4,0.2,8) = 0.450
・・・・・・・・・
y(3.4,0.2,19) = 0.842
y(3.4,0.2,20) = 0.452
また0.452と0.842のループに入りました。
よってグラフのc=3.4についてはy=0.452の位置とy=0.842の両方の位置に点を打つ。
- 2D．次に初期値x=0.3と取り、y(3.4,0.3,∞)。
答えは0.452と0.842のループになります。よってグラフの・・・
- ・・・・・・・・・
- 2X．次に初期値x=1.0と取り、y(3.4,1.0,∞)。
答えは0.452と0.842のループになります。よってグラフの・・・
-
- 終了
-
- どの初期値xから始めても0.452と0.842のループになります。
よってグラフ上ではc=3.4地点 → y=0.452＆y=0.842の2点になります。
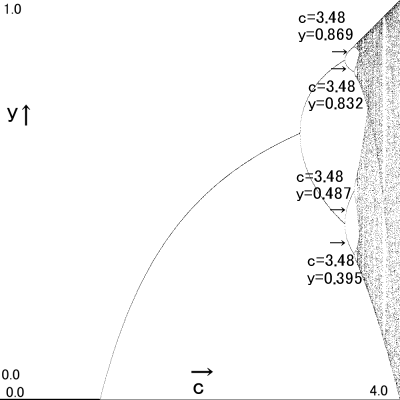
同様の計算でc=3.48の時は
どのxから始めても収束値は y= 0.395 → 0.832 → 0.487 → 0.869 → 0.395 → ・・・・
の4パターンループになり
グラフの線は対応した4本に分岐します。
次からカオスに入ります。
cの値が増えるにつれ分岐も複雑になり大変な事に・・・！
第1章へ 前章へ 次章へ 第7章へ
最新の日記へ
