よくわかるカオスとフラクタル。数学的解法の限界2(2010/01/01)

カオス図:
例えばc=0.5を取ります。
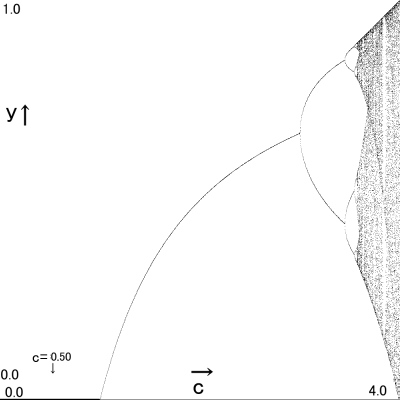
このcに対応するyは0.0ってグラフではなってますね。
この0.0がどこから出てきたか
具体的に計算します。
ルールを復唱。
y(c,x,0) = x
y(c,x,n+1)= c・y(c,x,n)・(1-y(c,x,n))
y(c) = y(c,x,∞)
c=0.00〜4.00、x=0.00〜1.00の範囲を動くとする。
- 1.まずはc=0.5と取る。
- 2A.次に初期値x=0.0と取る。
- 3A
y(c,x,0) = x
よって
y(0.5,0.0,0) = 0.0
- 3B
y(c,x,n+1)= c・y(c,x,n)・(1-y(c,x,n))
よってc=0.5、x=0.0、n=0の時に
y(0.5,0.0,1)= c・y(0.5,0.0,0)・(1-y(0.5,0.0,0))
y(0.5,0.0,1)= 0.5・0.0・(1-0.0)
y(0.5,0.0,1)= 0.0
- 3C
y(c,x,n+1)= c・y(c,x,n)・(1-y(c,x,n))
よってc=0.5、x=0.0、n=1の時に
y(0.5,0.0,2)= c・y(0.5,0.0,1)・(1-y(0.5,0.0,1))
y(0.5,0.0,2)= 0.5・0.0・(1-0.0)
y(0.5,0.0,2)= 0.0
- 3D
y(c,x,n+1)= c・y(c,x,n)・(1-y(c,x,n))
よってc=0.5、x=0.0、n=2の時に
y(0.5,0.0,3)= c・y(0.5,0.0,2)・(1-y(0.5,0.0,2))
y(0.5,0.0,3)= 0.5・0.0・(1-0.0)
y(0.5,0.0,3)= 0.0
- ・・・・・・・
- この後は何万回繰り返しても同じ計算なのでy(0.5,0.0,∞)は0.0に収束した。よってグラフのc=0.5、y=0.0の位置に点を打つ。
- 2B.次にxを少しずらし初期値x=0.1と取る。
どれだけxをずらすかは任意です。
細かく動かせば動かすほど精度の高い結果が出てきますので実際にはグラフを描画させるマシンのCPUパワーと相談と言うことになります。
ここでは0.1刻みで動かすとします。
- 3A
y(c,x,0) = x
よって
y(0.5,0.1,0) = 0.1
- 3B
y(c,x,n+1)= c・y(c,x,n)・(1-y(c,x,n))
よってc=0.5、x=0.1、n=0の時に
y(0.5,0.1,1)= c・y(0.5,0.1,0)・(1-y(0.5,0.1,0))
y(0.5,0.1,1)= 0.5・0.1・(1-0.1)
y(0.5,0.1,1)= 0.045
- 3C
y(c,x,n+1)= c・y(c,x,n)・(1-y(c,x,n))
よってc=0.5、x=0.1、n=1の時に
y(0.5,0.1,2)= c・y(0.5,0.1,1)・(1-y(0.5,0.1,1))
y(0.5,0.1,2)= 0.5・0.045・(1-0.045)
y(0.5,0.1,2)= 0.0215
- 3D
y(c,x,n+1)= c・y(c,x,n)・(1-y(c,x,n))
よってc=0.5、x=0.1、n=2の時に
y(0.5,0.1,3)= c・y(0.5,0.1,2)・(1-y(0.5,0.1,2))
y(0.5,0.1,3)= 0.5・0.0215・(1-0.0215)
y(0.5,0.1,3)= 0.00105
- ・・・・・・・
- この後に何万回も計算を繰り返してゆくと数字はどんどん小さくなってy(0.5,0.1,∞)は0.0に収束した。よってグラフのc=0.5、y=0.0の位置に点を打つ。
実際にはコンピューターの限界により∞回の再帰演算はできませんが
(例えば)1000回も繰り返せば実用上問題ない精度とし
y(0.5,0.0,1000)≒y(0.5,0.0,∞)として途中で打ち切り次のxに移動します。
- 2C.次に初期値x=0.2と取る。
- 同様の手順で
y(0.5,0.2,0) = 0.2
y(0.5,0.2,1) = 0.08
y(0.5,0.2,2) = 0.0368
y(0.5,0.2,3) = 0.0177
- ・・・・・・・
- この後に何万回も計算を繰り返してゆくと数字はどんどん小さくなってy(0.5,0.1,∞)は0.0に収束した。よってグラフのc=0.5、y=0.0の位置に点を打つ。
- 2D.次に初期値x=0.3と取り、y(0.5,0.3,∞)。答えは.0.0になります。よってグラフのc=0.5、y=0.0の位置に点を打つ。
- ・・・・・・・・・
- 2X.次に初期値x=1.0と取り、y(0.5,1.0,∞)。答えは.0.0になります。よってグラフのc=0.5、y=0.0の位置に点を打つ。
-
- 終了
-
- 実際にはどの初期値xから始めても最終収束点y(0.5,x,∞)は全て0になるので、
グラフ上でc=0.5地点 → y=0.0になるんですね。
いかがでしたでしょうか・・・
答えが0じゃつまらないので今度は別のcでもう一回やります。
c=1.5を取りましょう。
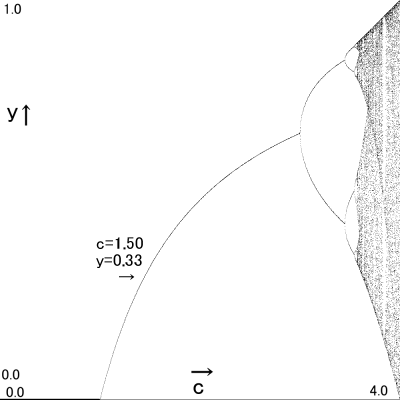
グラフではこれの対応するyは0.33ってなってますね。
この0.33はどうして出てきたかまた計算します。
- 1.まずはc=1.5と取る。
- 2A.次に初期値x=0.0と取る。
なおx=0のケースだけは以下に示すよう全てのy(c,x,n)でy=0になりますので「つまらない」初期値とし今後は無視とします。
x=0だけは例外です。
- 3A
y(c,x,0) = x
よって
y(1.5,0.0,0) = 0.0
- 3B
y(c,x,n+1)= c・y(c,x,n)・(1-y(c,x,n))
よってc=1.5、x=0.0、n=0の時に
y(1.5,0.0,1)= c・y(1.5,0.0,0)・(1-y(1.5,0.0,0))
y(1.5,0.0,1)= 1.5・0.0・(1-0.0)
y(1.5,0.0,1)= 0.0
- 3C
y(c,x,n+1)= c・y(c,x,n)・(1-y(c,x,n))
よってc=1.5、x=0.0、n=1の時に
y(1.5,0.0,2)= c・y(1.5,0.0,1)・(1-y(1.5,0.0,1))
y(1.5,0.0,2)= 1.5・0.0・(1-0.0)
y(1.5,0.0,2)= 0.0
- ・・・・・・・
- この後は何万回繰り返しても同じ計算なのでy(1.5,0.0,∞)は0.0に収束した。よってグラフのc=1.5、y=0.0の位置に点を打つ。
- 2B.次に初期値x=0.1と取る。これからが本番。
- 3A
y(c,x,0) = x
よって
y(1.5,0.1,0) = 0.1
- 3B
y(c,x,n+1)= c・y(c,x,n)・(1-y(c,x,n))
よってc=1.5、x=0.1、n=0の時に
y(1.5,0.1,1)= c・y(1.5,0.1,0)・(1-y(1.5,0.1,0))
y(1.5,0.1,1)= 1.5・0.1・(1-0.1)
y(1.5,0.1,1)= 0.135
- 3C
y(c,x,n+1)= c・y(c,x,n)・(1-y(c,x,n))
よってc=1.5、x=0.1、n=1の時に
y(1.5,0.1,2)= c・y(1.5,0.1,1)・(1-y(1.5,0.1,1))
y(1.5,0.1,2)= 1.5・0.135・(1-0.135)
y(1.5,0.1,2)= 0.175
- 3D
y(c,x,n+1)= c・y(c,x,n)・(1-y(c,x,n))
よってc=1.5、x=0.1、n=2の時に
y(1.5,0.1,3)= c・y(1.5,0.1,2)・(1-y(1.5,0.1,2))
y(1.5,0.1,3)= 1.5・0.175・(1-0.175)
y(1.5,0.1,3)= 0.216
- 3E
y(1.5,0.1,4)= 1.5・0.216・(1-0.216)
y(1.5,0.1,4)= 0.255
- 3F
y(1.5,0.1,5)= 1.5・0.255・(1-0.255)
y(1.5,0.1,5)= 0.285
- 3G
y(1.5,0.1,6)= 0.305
y(1.5,0.1,7)= 0.318
y(1.5,0.1,8)= 0.325
y(1.5,0.1,9)= 0.329
y(1.5,0.1,10)= 0.331
y(1.5,0.1,11)= 0.332
y(1.5,0.1,12)= 0.333
y(1.5,0.1,13)= 0.333
- ・・・・・・・
- この後に数字は動かなくなりy(1.5,0.1,∞)は0.333に収束した。よってグラフのc=1.5、y=0.333の位置に点を打つ。
- 2C.次に初期値x=0.2と取る。
- 同様の手順で
y(1.5,0.2,0) = 0.200
y(1.5,0.2,1) = 0.240
y(1.5,0.2,2) = 0.298
y(1.5,0.2,3) = 0.314
y(1.5,0.2,4) = 0.323
y(1.5,0.2,5) = 0.330
y(1.5,0.2,6) = 0.332
y(1.5,0.2,7) = 0.333
y(1.5,0.2,8) = 0.333
- ・・・・・・・
- この後に数字は動かなくなりy(1.5,0.2,∞)は0.333に収束した。よってグラフのc=1.5、y=0.333の位置に点を打つ。
- 2D.次に初期値x=0.3と取り、y(1.5,0.3,∞)。答えは.0.333に収束します。よってグラフのc=0.333、y=0.0の位置に点を打つ。
- ・・・・・・・・・
- 2X.次に初期値x=1.0と取り、y(1.5,1.0,∞)。答えは.0.333に収束します。よってグラフのc=0.333、y=0.0の位置に点を打つ。
-
- 終了
-
- 実際にはどの初期値xから始めても最終収束点y(1.5,x,∞)は全て0.333になるので、
かくしてグラフ上でc=1.5地点 → y=0.333になります。
このような手順を持ってグラフは描かれます。
面白いのはcが3.00を超えた後です。
グラフで見ると線が分岐してますね。
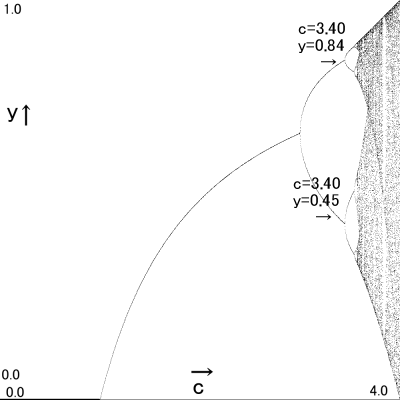
これは値の収束値が二つ以上ある事を意味します。
次のページでもまた具体的な計算を示して
なぜ2つの値が出るのか、なぜグラフは分岐するかを説明します。
第1章へ 前章へ 次章へ 第7章へ
最新の日記へ



