数学界に大論争を呼んだ選択公理

数学界に大論争を呼んだ選択公理(2/2) 2015/01/12

さて、結論から述べますが
その後、ゲーデルの研究により
　「選択公理に（通常の環境下では）矛盾は含まれない、すなわち使って問題はない」
事がわかりました。

具体的にはゲーデルは「構成可能集合L」を考えました。

「構成可能」とは・・・
いわゆる「定義できる」の事です。

これまた以前にもした話ですが
数学と言うのは
　「数とは何か。数学V宇宙の脊髄を自然数が走る。第4章」で
した話ですが

数学と言うのは「空集合 = {}」から始まって、
空集合の上に選択を作って
S₀ ＝空集合 = {}
S₁ ＝ 2^S₀ = {}, {{}}
S₂ ＝ 2^S₁ = {}, {{}}, {{{}}}, {{},{{}},}
S₃ ＝ 2^S₂ = {}, {{}}, {{{}}}, {{},{{}}}, {{{{}}}}, {{},{{{}}}}, {{{}},{{{}}}}, {{},{{}},{{{}}}}
S₄ ・・・・・
のような各階層nに2ⁿのメンバーを持つピラミッド階層型に構築します。

数学的に考察可能な対象、
例えば「数字」、「二次元」、「面積」、「π」、などのなんらかの「値」的な性質を持つ
ありとあらゆる物体は
このピラミッドの中に出てきます。
（正確に言えば、同じ性質を持つサブ構造をWの中に発見できる）

このS_n全体を集めた物をWと呼びます。

（Vと呼ぶ場合もあります。
　通常はV＝Wとなるのでそれほど区別する必要もありませんが。

　厳密にはV＝全集合のクラス
　W＝well-founded（矛盾がないように、ピラミッド型によく構築された構造）。の意味合い。
　Vが性質的な要請で、Wがその要請を満たした具体的なモデルです。
　Vは矛盾排除のためwell-foundedな性質を要求する必要が必ずありますし、
　well-foundedな性質を持たせるとWができあがるので
　通常はV＝Wに勝手になっちゃいます。

　ただしときどきは後述のV＝Lのような別の世界観もある）

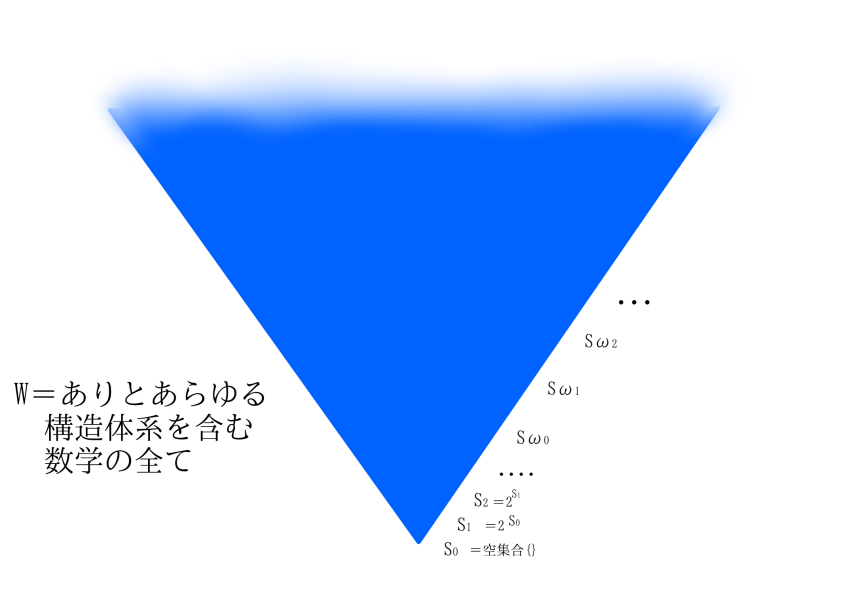
Wは数学の完全体。数学の学問としての全ての研究対象はこの中に詰まっています。

逆に言えば、Wに属さない構造を持った集合は矛盾を孕む可能性があるので
（例：ラッセルの集合。 R = {x:R∉x}）
数学としては研究の対象になりません。

少なくともいまの数学にある問題・難題・研究対象としての構造は全てWの中で表現できるので
W以外の構造を考察する意味はほとんどありません。
実質的に「W＝数学全体の考察対象」が
現代数学のデファクトスタンダードと言えます。

ただ・・・・実際はちょーっと違うんですねー^^;

と言うのも数学を扱うのは人間であり、
人間が書けるのは文字であり、
文字数には限界がある。

すなわちいくらWが数学の完全体と言っても
その中で「有限の長さの文章で記述可能な対象」の範囲でしか
人間には現実的に考察可能でありません。

例え宇宙が無限に広いと言っても、人間の目で観測できる範囲にしか
人間には知る術はなく、
手の届かない範囲は学術的に全くタッチできないんです。

座標を記録するにしたって必ずスペースの問題がある。
無限の座標を紙・ノート・PC・HDDに書くってのは不可能で、
必ず有限個に厳選しなければいけない。その範囲でしか我々は作業できない。

ゲーデルはそれを厳密に考察して
「構成可能集合L」を構築しました。

LはWのサブセットで、
Wの中から「人間が有限の文章で記述できる範囲」に絞った物と考える事ができます。

そしてLはWに比べると、相当シンプル化されています。

その理由としてはまあルベーグ積分的なアイディアに似ており
すなわち人間には文字が有限である以上
せいぜいω₀程度の複雑さを持った構造、もしくは方程式しか記述できないんですね。

それらω₀程度の複雑さを
いくら集めてもω₀程度の複雑さにしか
成り得ないし、
結局ω₀複雑さがLの上限。
人間に記述できる数学の上限になる。

と、Lおよび人間の限界を示したことです。

そしてLは選択公理をみたします。
その理由としてはLはω₀程度の複雑さしかないので。
ω₀複雑さから選択した結果はω₀複雑さの
中に留まる。問題をいま以上に難しくしないのでOK．

---------------

さて。
我々が本当に恐れていたのは選択公理の無差別性。
すなわち到達不可能基数や巨大基数に対しても
選択を行えてしまう強大無比なパワーだったのですが
それは杞憂に終わりました。

なぜなら人間に記述できる数学はLが上限。

Lの中だけで考えていればいいし、
どう頑張ってもL以上の考察は無理なので、

Lの範囲を超える到達不可能基数サイズや巨大基数サイズの集合に対して選択公理を適用すると言った状況は
通常の数学をやってる上ではまず永遠に
訪れないとわかったからです。
（やろうと思えばできます・・・しかし巨大基数用の追加公理が必要でこれはかなり異端になる）

ちなみに・・・はい。
到達不可能基数サイズを持つモデルの中には
選択公理の否定、すなわち選択公理からパラドックスを導くモデルもあります。
（コーエン1960年の論文）

もっともそのモデルと言うのはω₀より高い複雑さを持つ物体であり、
人間文字によっての具体的な記述は不可能。
具体例を誰も作れない以上
やはり考える必要はありません。（´д｀;
（人間には記述できないが、あると言うことは証明できる）

---------------

この「記述可能性」ってのは現代数学においては結構重要な問題でして、

これまた前に私がやったガロア理論と、5次元方程式の解法の不可能性のお話
や、
よくわかるカオスとフラクタル数学的解法の限界

などもこの一種なんですが。

つい400年ぐらい前までは数学界では「どんな問題でも解けるはず。解けないのは研究が足りないからだ！」って
超絶イケイケな風潮でしたが^^;
ここ100年ぐらいは数学の限界性、
　「・・・・いやちょっと待って。ひょっとして、無理。この問題は解けない・・・・んじゃないか・・・？」
がまこと活発に議論されてます。

NP問題だったり、カオス問題だったり、整数論問題だったり。
解けない物は解けない。恐らく解法が存在しないんじゃないだろうかってわかってきました。

それは例えば
　「一般5次元方程式の解は、√を使う方法だけじゃ記述できない」
と判明したように、
　「○○問題の解および証明は、人間の扱うL数学では記述できないのでは？」
ってのと同じで、人間がL数学とω₀複雑性に縛られてる以上は証明できる範囲に限界があるんです。（´д｀;

あ、ただしゲーデルの完全性定理があるので「正しい事柄＝必ず証明できる方法がある」ってのはわかるのですが。
依然としてその「正しい事柄」かどうかの判定が、人間のL数学でできるのか？
って問題になるわけでして。

恐らく、多くの整数論関係の問題なんかはNP問題的な性質、
すなわち「全ての数字のパターンを調べつくす」以外の方法はない性質を持ち、
そして「全ての数字を調べる」事は人間にはできないので
「有限の行数では証明（判定）に到達できない」と私は思ってます。(^_^A;

そうなると「有限の行数では証明を得られない」、証明不可能性を示す手順/システム/アルゴリズムが必要になったり。
いやそれすらもL数学には辿り着けないのかも。

いずれにせよ人間（数学）は非常に非力で、W全体のほんの僅か僅か僅かしか
知ることができないと言うのは
現代の集合論的見地からは妥当と言えるのではないでしょうか？

---------------

まとめると：
　・選択公理は完全無矛盾ではない。適用すると矛盾の発生するモデルもある。
　・が、そのモデルはL以上の複雑さを持っており、人間には記述不可能。
　・人間の記述できる数学、構築可能集合Lの中では選択公理は無矛盾
　・よって実質的には選択公理を「（通常の環境下では）矛盾を含まない」、
　　絶対的な真理、
　　公理として採用することには問題はない。

ってな事がその後の研究でわかり、
晴れて選択公理は無矛盾。常に真として成立する絶対的な真理。
集合論の公理の1つとして採用する至りとなったわけです。

ご拝聴ありがとうございました。

前ページ

トップへ