数とは何か。数学V宇宙の脊髄を自然数が走る。 第4章
しかし寂しいですね。
いまこの世界では唯一、空集合
{}
だけが存在しています。
もうちょっと仲間が欲しい。
そこで何をするかと言えばZFCの中から
を使います。
これを日本語にすれば「集合を格納した、新たな集合を作れる(箱を納めた、新しい箱を作れる)」
って事です。
そして空集合{}にこれを適用すれば新たな集合
{{}}
が誕生します。
それに最初から居た空集合{}を加えて合計二名を第2階層のメンバーとします。
次にまた冪集合を第二階層メンバーに適用することで次の世代の箱in箱を作り、および対集合で全組み合わせパターンを羅列することで
(わかりやすくするために集合は赤で囲い、集合の間の区切りは黒いコンマで表記します)
第1階層:
{}
第2階層:
{},
{{}}
第3階層:
{},
{{}},
{{{}}},
{{},{{}},}
第4階層:
{},
{{}},
{{{}}},
{{},{{}}},
{{{{}}}},
{{},{{{}}}},
{{{}},{{{}}}},
{{},{{}},{{{}}}}
・・・・
第n階層の人口は2n-1人と言うふうに増えてゆきます。
このようにしてたった一つの空集合
{}
から始まった世界も新しい箱の中に古い箱を色々な形で納める方式でどんどん新種が生まれて広がって行きます。
この拡張してゆく世界をVの形に見立てて数学ではこの世界を一般的にVと表記します。
イメージ図:
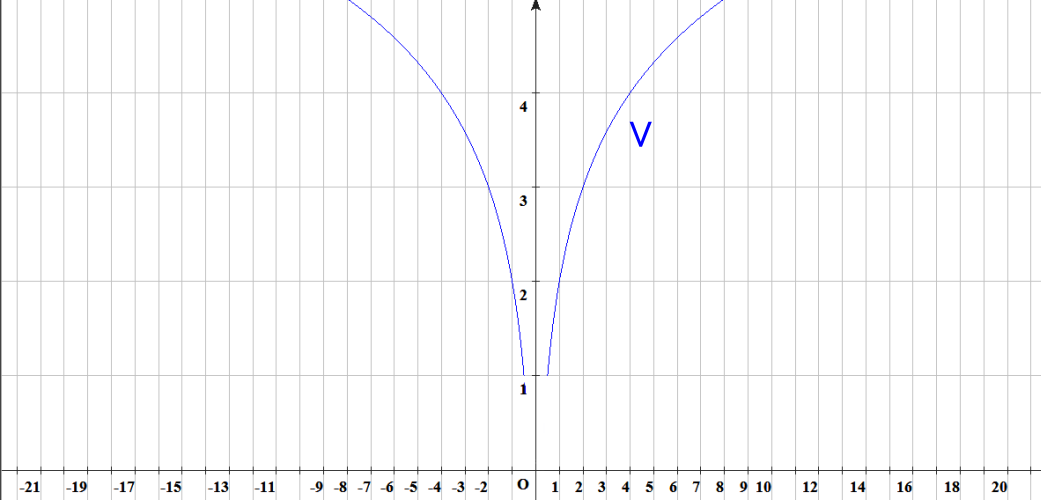
n=(log(abs(x))/(log(2)))+2
で描いた図形。
各nの断面でできる線の広さが2n-1になっています。
注:あくまでイメージです。
Vの名前の由来は示すために描いただけで
Vは2次元の形に広がってるとかそういう意味には取らないでください。それにnは整数値しか取れない飛び飛びですので本来はグラフにもなりません。
このVの時点ではまだ「数」は存在していません。
存在するのは{},
{{}},
{{{}}},
{{},{{}}},
{{{{}}}},
{{},{{{}}}},
{{{}},{{{}}}},
{{},{{}},{{{}}}}のような{}だらけの気味の悪い物体ばかり(A^^;
しかしこいつらは数学の基幹に存在する物体であり
ベースとなる万能ブロック素材。
数学における全ての大抵の固体は
この{}共の中から数を作り出せるのです。
さて話を第1章に戻しますが数とは、集合の特殊なケースです。
どういう事でしょうか。
いや、そもそも『数』ってなんでしょうか。
説明を簡単にするために
まあ答えから言っちゃうと(^^;
数とは「全比較可能な集合」です。
比較とは数の大小関係です。
1≦1000
1000≧333
3000≦56789
のように全ての数Aと全ての数Bの間に≧または≦の関係が成り立ちます。
(数学では一般に「比較、または包括」と言えば≦または≧の事です。
数学の問題を扱う上ではまず大抵のケースで「同一、または大きい」ばかりが出てきて
>または<のような同一を含めないケースはほとんど出てこないので)
こう書かれると「比較できる?そんなの当たり前じゃん」と思ってしまうかも知れませんが
実は意外なんですよこれって。
「比較関係」の言葉を変えて「包括関係」を考察してみます。
包括とは「集合Aのメンバーは集合Bのメンバーを全て含む」の意味で、
例えば
{A,B,C}⊃{B,C}
{馬,象}⊂{馬,キリン,象}
など。
いかにも≦や≧にそっくりでしょう。ほとんど大小の関係にも見えますし。
ところがしかし
例えば{A,B,C}と{C,D}の間には⊂も⊃もどちらも存在できません。
×{A,B,C}⊃{C,D}
×{A,B,C}⊂{C,D}
ですので。
包括とは「片方のメンバーが、相手のメンバーを全て含む」事であって
一部分のメンバーを含むだけでは包括とは言えません。
それどころか
{A,B,C}⊃{B,C}
{A,B,C}⊃{A,C}
などは成り立っても
{B,C}と{A,C}間には包括関係が成り立たないなど、
一般的に集合の世界では包括が成り立つケースの方がレアと言えましょう。
なので「全ての数字mと、全ての数字nには比較関係≦または≧のどちらかが必ず成り立つ」
と言うのは結構どころか物凄い特殊な事なのです。
数字の本質は数字そのものにあらず!単体では意味のないただのシンボルです。
そこに他の数字をもう一つ持ってきたときに比較関係が確実に成り立つ事、
「(他者との)比較確実性」こそが数の正体、本質だったのです。
さて話をV世界に戻しましょう。
ここでも包括関係は所々で
{{}}⊃{}
{{{}},{{{}}},{{{{{}}}}}}⊃{{{}}}
のように成り立ち、
逆には
{{{}}}と{{},{{{}}}}のような⊃も⊂も成り立たないような二者もあります。
むしろほとんどのケースで包括関係は成り立ちません。
ところがこの中からメンバーを厳選して、とある属性だけをもった奴らを抜き出すと
そいつらの間では⊃か⊂のどちらかが確実に成立する包括確実性が生まれるのです。
具体的に挙げましょう。
それはこいつら。
N={{},{{},{{}}},{{},{{}},{{{}}}},{{},{{}},{{{}}},{{{{}}}}},・・・・}
帰納法で
1.N1 = {}
2.Nn = Nn-1 ∪ {Nn-1}
3.N = N∞
すなわちNnの要素は(Nn-1までの要素全部)+(Nnを箱に格納した要素)で
作ってゆく。
このクラブNのメンバー間に限ってはどの二者をとっても
{}⊂{{},{{}},{{{}}}}
{{},{{}}}⊂{{},{{}},{{{}}},{{{{}}}}}
{{},{{}},{{{}}},{{{{}}},{{{{{}}}}}}}⊃{{},{{}},{{{}}},{{{{}}}}}
のように必ず⊃か⊂のどちらかが成り立つのです。
すなわち包括確実性。
ついに見つけた、こいつらが「数」に相当する物体です。
後は単純にラベルの貼り替えで
[{}]→0
[{{},{{}}}]→1
[{{},{{}},{{{}}}}]→2
・・・
のように識別し、さらに包括関係も
⊂→≦
⊃→≧
とラベルを貼り替える。
そうすれば上記の式も
{}⊂{{},{{}},{{{}}}} → 0≦2
{{},{{}}}⊂{{},{{}},{{{}}},{{{{}}}}} → 1≦3
{{},{{}},{{{}}},{{{{}}},{{{{{}}}}}}}⊃{{},{{}},{{{}}},{{{{}}}}} → 4≧3
になり、数の世界を再現できます。
そしてNも読み替えれば
N={0,1,2,3,4,・・・・}
となりこれで自然数コレクションができてました。
第一章で書いた
「数の世界、および法則」と言うのは「集合の世界、および法則」の一部分であり、
数とは集合の特殊なケースとして成立する
とはこの事です。
自然数さえ構築できれば後は簡単。
自然数を二倍して1:1で+と−に分配してゆけば整数になりますし、
m/nを(m,n)、すなわち整数の軸を持つ二次元の座標として識別すれば有理数になります。
無理数はちょっと面倒ですがデデキント切断という物を導入して「有理数でカットして、はみ出た残り」として識別すれば出てきます。
そして有理数と無理数を混ぜれば実数の完成。
実数にベクトルと群を導入し二乗すればマイナスになる要素をくっつければ虚数・複素数の完成。
自然数を元に加工した操作で後はいくらでもトントン拍子に作れるんですね。
最後に数学宇宙Vと自然数コレクションNの関係を述べて終わりにしましょう。
前ページへ 次ページ
トップへ
