ガロア理論と、5次元方程式の解法の不可能性のお話
「ガロア理論と、5次元方程式の解法の不可能性のお話(2006/12/22)」
あちこちの店や仕事が休みになってなにかと寂しくなるこの年末・年始時期。
空き時間ができるとどうにも暇になりがちですよね。^^;
少しでも解消になればと年越しで少し面白い雑談をしてみます。
お題は「5次元方程式の解法の不可能性」
まず中学生の頃を思い出して二次元方程式から始めてみましょう。
すなわちaX2+bX1+c=0です。
この時の答えは
X=(−b±√(b2-4ac))/2a
でしたね。中学校の頃に誰でも習います。
人によっては思い出すのも嫌な式。^-^;
中学・高校では二次元方程式まででおしまいでその先の話はしませんでした。
それでは三、四、五・・・次元方程式の解法は今どこまで解明されているか歴史も含めてちょっと紹介。
二次元方程式の解法が発見された後に
人は自然と三次元方程式:aX3+bX2+cX1+d
の解法も追い求めました。
そしてそれは西暦1500年代にカルダーノのと言う人に発見されました。
公式はかなり長くなるのと、中身その物は正直あまり興味を引くような物はなくただ長いだけのような物なので
一般に紹介される事はありませんが確かに存在します。
そして四次元方程式:aX4+bX3+cX2+dX1+e
もそのすぐ後、同じく西暦1500年代にフェルラーニによって解かれ公式が発見されました。
同じくただ長いだけであまり面白くないので書きませんが。
その後に五次元方程式:aX5+bX4+cX3+dX2+eX1+f
の解法を求める旅が始まったのですが・・・これが見つからない!!
実際その後200〜300年も世界中のたくさんの人が挑戦して気の遠くなるような労力が
費やされましたが誰も成功せず
「もしかして五次元方程式の解の公式って存在しないんじゃ・・・?」と考えられる
ようになり、
そしてついに西暦1800年代にアーベルによって正式に「五次元方程式の解の公式は存在しない(表記できない)」と証明され、
当然五次元の解法がないのだから六、七、八、・・・以降も解法がない、
すなわち四次元までで打ち止めである事がわかり方程式の解法の探求にはここに完全な形で終止符が打たれました。
どうでしょうか。面白そうな話だと思いませんか。
一,二,三,四次元方程式までは答えが出せるのに5次元方程式になると
公式が存在しないのです。
と、言うか正確には、答えが存在する事は間違いないのですが
問題はその答えが四則演算とルートを使う方法では決して書けない類の性質を持つ数であるので
公式を書きたくても書けないのです。
ここら辺の訳と事情を説明したいと思います。
数学のジャンル的にはガロア理論と呼ばれる分野です。
(ガロア理論自体は体の拡張における基礎体・中間体・拡張体と、拡張によって固定される元のオートモーフィズム群の相関を説明する理論なので
五次元方程式を直接説明する物ではありませんが・・・歴史的にもそうやって発展してきたので一般的には方程式の解法と言えばガロア理論で呼ばれます。)
詳細な証明までするとなると専門書を数冊並べないといけないような難解な理論なのでここでは省きますが・・・(´д`;;;物っ凄い大変
(今から本を買ってきて勉強し始めても間違いなく一朝一夕でどうにかなるようなレベルじゃありません。昔の人が到達するのに300年を費やした理論です・・・)
なるべく直感に訴える「なんでこうなってしまうのか」のエッセンスだけでも次回から。
「ガロア理論と、5次元方程式の解法の不可能性のお話 - 2(2006/12/25)」
それでは前回の続き。解法のほどを。
「五次元方程式の解は存在するが、その答えを四則演算とルートを使うだけでは記述できない。」が議論のキモです。
まずここの意味をわかりやすくしたいと思います。
簡単な例えを出してみます。
例えば「1.5」と言う数字を作りたいとき、
(なんでもいいから整数からスタートして)足し算・引き算・掛け算だけを使い
1.5と言う数字を作る事はできません。
+ー×の演算は整数で閉じているのでどこをどうやっても
小数(分数)を作る事はできないのです。
少なくとも「割り算」と言う手法を導入しない限り小数の数は絶対に整数同士の演算を繰り返しているだけでは作れません。
原理的にはそれと同じと言っていいです。
5次元方程式には確かに解が5つ存在しているのですが、
(分数に)四則演算とルートを組み合わせる方法ではどこをどうやっても
作る事のできないレベルにある数なんです。
ちょうど+−×だけでは1.5を作れなかったように。
なぜ「四則演算とルートでは五次元方程式の解を書けないのか?」の方が本題ですが
かなり難しいですが何が起こっているか程度は説明できると思います。
まずQを有理数全体の集合とします。
1+√2などルートを使って表現すると言うのは
これに適当な数nのルートをつけQをQ(√n)に拡張すると言う事です。
なのでルートを使って拡大を繰り返す事、それはすなわち
集合の拡大連鎖
Q=K=K0⊂K1⊂K2⊂K3・・・
を昇鎖を作ることです。
具体的には、
Q=分数で書き表せれる数全て
K1=分数と√2を使って書き表せれる数全て
K2=分数と√2と√3を使って書き表せれる数全て
K3=分数と√2と√3と√5を使って書き表せれる数全て
・・・・
のように分数を基礎にしてルートを次から次へと追加してその中で書き表せれる数を次から次へと拡大して作ってゆくのです。
この時に一回一回の拡大は「巡回的正規」と言う性質を持っています。
これは√の性質が比較的単純な所から来る物で、√を追加して集合を拡大する作業は
綺麗に行儀よく振る舞ってくれます。
すなわち√を繰り返して集合を拡大する作業は「巡回的正規(左右対称)拡大を繰り返す」と言う事です。
逆に言うと「0から始まって巡回的正規列昇鎖の積み重ねによって到達できる物は分数+四則演算+ルートで表記可能、
0から始まって巡回的正規列昇鎖の積み重ねによって到達できない物は表記不可能。」なわけです。
ここが議論の山なのですが
三次元方程式の解の集まり(のガロア群)はS3と言う群を作り、そしてS3には
S3→A3→0 (→は巡回正規列部分群を表す)
と言う巡回的正規部分群の連鎖を持ちます。
なので先ほどの議論により分数+四則演算+ルートで表記可能。
四次元方程式の解のガロア群もS4と言う群を作りそれも
S4→A4→V4→U2→0
の巡回的正規部分群連鎖を持つので分数+四則演算+ルートで表記可能
一方五次元方程式のガロア群はS5を作るのですが
S5→A5 ×××(巡回的正規部分群を持たない)××× →0
のようにA5群は巡回的正規部分群を一つも持たないせいで
ここだけS5(=解)まで0から巡回的正規部分群連鎖を積み重ねて到達する道がありません。
よって分数+四則演算+ルートで表記不可能
となります。
(わかりやすさを最優先するために理論や単語の使い方とかはあえて支離滅裂に書いてますが細かいツッコミはしないでください。)
一言で言うと、
「ルートを付け足すという行為は、巡回的かつ左右対称な、そんな形の拡大を繰り返す行為なのだが、
五次元方程式の解の集まりは巡回的左右対称な形の積み重ねの形をしていないので、
ルートをいくら追加しても作りようがない。」
こんな感じになっているのを掴めたらOKです。
これが五次元方程式の解は分数と四則演算とルートでは決して表記する事のできない理由です。
答えは確かにあるのに(ルートを使うような方法では)決して書く事ができないんです。
何かしらルートよりもっと複雑な性質を持つ、非巡回的・非左右対称な形の拡大を行える物を演算を使わない限りは。
では、なんでS3、S4は大丈夫でS5で途切れるのかと言うと
「そうなっちゃう」としか言いようがないですが。^^;
2、3、4段までは巡回的正規の積み重ねでうまくいきましたが
5段目は広くなりすぎて手に負えなくなったとしか・・・
次回は正規性についての補足をします。
なにしろここが議論の中核ですので。
「ガロア理論と、5次元方程式の解法の不可能性のお話 - 3(2006/12/29)」
群用語で部分群HがGに対して正規的であるとは、
gH=Hg {∀g∈G}
が成り立つ事ですが、
体論にもこれに相当する正規性拡大と言う物があります。
(体の拡大とそのガロア群は一対一で対応するので実際には同じ物を別の視点から見ているだけですので。)
これは一言で言っちゃえば
「解が一つ得られる時に他の解も全て得られる」と言う意味です。
例えば2次元方程式、
X2-2=0
の場合にはα=√2が答えで、もう一つの答えはβ=-√2で
この時はβ=(-1)×(α)が成り立つので基礎体KをK(√2)に拡大してαが得らればβも同時に必ず得られます。
実際二次元方程式の一般解はX=(−b±√(b2-4ac))/2aですから
√(b2-4ac))を基礎体に追加すれば根が全部見つかる事は保証できます。
なので二次元方程式の根は常に正規です。
ところが
しかし三次元方程式の
X3-2=0
とかになると答えはα=21/3、β=ω・21/3、γ=ω・21/3 (ω=(-1+√-3)/2))
で見られる用にルートを使う項目は21/3と√-3の二つが現れます。
よってαに出てくるルートを取って基礎対をK(21/3)のように拡大しても
√-3がまだないので残りのβ、γは得られません。
これが正規ではない(一つの解を得ても他の共約解はまだ得られない)解が現れると言う現象です。
12/25の記事では
> すなわち√を繰り返して集合を拡大する作業は「正規的拡大を繰り返す」と言う事です。
と書いてしまいましたが、実はウソです。^^;
√を足す拡大は上記でみたように一般的には(実際ほとんどの場合は)正規的にはなりません。
ただしところが、ここで順番を変えて、
追加するルートは21/3→√-3と行くのではなく
その逆にまず√-3を追加してK(√-3)を作ってから
(√-3は二次元方程式F(x)=X2+3=0などを満足させる解で、
√-3があればF(x)のもう一つの解である-√-3も得られるのK(√-3)/Kは正規拡大。
その後にK(√-3)をもう一段階拡大してK(√-3,21/3)を作れば
(K(√-3,21/3)/K(√-3))も正規拡大になります。
なぜならこんどは直前の基礎体に√-3があるのでαが現れると同時にβ、γも作れるようになったからです。
なので、√による拡大の操作その物はかならず正規拡大になるとは限りませんが、
順番を変えてうまくとってゆけば正規拡大の繰り返しになる方法が存在するので、
結果的に最終的に出来た拡張体は正規的拡大の昇鎖になると言うのが本当に意味です。
実際にはもっと強い要請の巡回的正規列と言う物を作ります。
なので前文は言い換えて
>> すなわち√を繰り返して集合を拡大する作業は「(順番をうまく取れば)巡回的正規拡大を繰り返す連鎖となる」と言う事です。
とでもしましょう。
これはルートにまつわる性質で、ルートを繰り返す拡大作業はどこをどうやっても
その内部のどこかに巡回的正規列のチェーンができてしまいます。
問題は「なんでそんな都合のいい順番がある事が保証されるの?」って事ですが・・・
そこが証明のポイントの山場の一つで、ルートによる体の拡大の構造の本質を突いたものっすごいシャープなポイントです。
さてここでいったん休んで、まず問題を整理する為の今の状態を明記してみましょう。^^;
それは:
Kを基礎体、
LをKの上にルート拡大を積み重ねて作った拡大体
とした時に、なぜガロア群(L/K)には巡回的正規列連鎖がある事が保証されるか?
です。
さっき見たように一般的に√拡大は正規的になるとも限らず、
たまたまうまい順番を選んだら正規的拡大のチェーンがあるのを見つけただけです。
ではなぜそんなチェーンがルート拡大の中に存在する事が保証されているのか?
なにしろありとあらゆる任意の√の取り方に対して存在を保証しろと言っているのですから
えらい問題です。
かなり途方に暮れます。こんな難しい問題どうやれってんだ・・・
しかしうまいやり方がある物で、
それはKとLの他に、Kに1の原始n乗根を加えたMを入れて考察します。
すると以下の図のような事が起こります。
(以下に使う可解群と言う言葉は「巡回的正規列のチェーン」と言う意味です。)
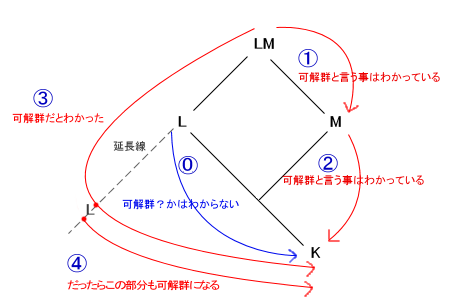
Mはなにしろ原始n乗根、別の言い方では複素数平面の半径1の円のn等分点で
非常にわかりやすくてシンプルな性質(確実に巡回的)を持っているので
1.LM/Mが可解群になるのは簡単にわかる事、
2.同じ理由でM/Kが可解群になる事も簡単、
3.その二つを繋げたLM/Kは当然可解群。
ここまでは瞬時にわかります。すると
4.L/KはLM/Kの商群。可解群の商群は可解群なのでL/Kも可解群。
QED
が成り立つことになりビックリするぐらい簡単に証明できてしまいました。
何が起きているのかもうちょっとまともな言葉で説明しますと、
K→Lを考えるのは難しすぎるので、KとLの中間に原始n乗根のMと言う抜け道ポイントを打って
K→Lに進む代わりにもっと簡単な登山ルートのK→Mへ進む。
しかもさらにLの標高を通り越してM→LMまで昇ってしまい、そこから下を眺めれば
K→M→LMルートは可解群だった。なのでK→LMは可解群。
K→L→LMも途中の道が違うだけで結局は同じK→LMなんだから可解群。
K→L→LMが可解群ならその途中の道のK→Lも可解群だろ。
って言っているわけです。
ガロア理論の本には必ず載ってる(この界隈では)有名な図ですが
私の中で初めてここの所の意味を理解した時は感動しました。
(数学と言うのは講義で教えられても本で読んでもこのレベルになると一回目ではまず理解できません。(少なくとも私程度の頭では・・・)
みんな意味はさっぱりわからなくても講師の言った事を機械的にノートに書き写して、
意味はわからなくても公式を活用して変形して問題を解いて(←何をしているのか本人も実はわかってない)、
それから頭の中で熟成が進んで?数週間〜数ヶ月〜数年遅れてから直感による理解が追いついてくるものです。^^;;;)
L/Kについては全然わかんなくても原始n乗根でポイントMを打って迂回してLMまで先回りしてからバックで戻ればL/Kの事は調べられる。
なんじゃこりゃ。
すごい。よくこんな頭のいい証明方法を見つけた物です。
あの難問が論理の本質をつけばわずか4行で撃沈するんですから・・・
以上にして√を繰り返して集合を拡大する作業は必ず「可解群のチェーンが存在する。」がわかりましたので、
逆に巡回的正規列(チェーン)を持たない事がわかっているA5は√によって作り得ない。
すなわち√と四則演算だけによる五次元方程式の解の表記不可能性が証明されるわけです。
こうして問題の全ては群論に還元されるわけですが要するに構造が違うのです。
ルートが□だとすればA5は○と思ってください。
四角いパーツをどこをどう組み合わせても丸は作れないように
絶対に構築できないんです。
ガロア理論による証明はいかがでしたでしょうか。
「あ、そっか」とやり方を言われてみればそりゃ当たり前なんですが・・・
実際人類が五次元方程式の解の考察を始めてからこの証明を見つけるまでに300年間を要しました。
一生考えてもたどり着けずに悔やみながら倒れた数学者もいたでしょうし
死屍累々たる犠牲と一生をかけて真理を追い続けた執念の果てに掴んだ論理の積み重ねの上に現代数学は成り立っています。
最新の日記へ
