無限にも大きさのランクがある!4(2009/01/01)
では非可算個無限は可算個無限と比べてどれぐらい大きいか?と言えば
そりゃもう圧倒的なんです。(^^;
可算個無限を2倍、3倍、10倍、100倍、1億倍、1000兆倍、100000000京倍、・・・・
しても非可算個無限には追いつきません。
実際(可算個無限 × 可算個無限 × 可算個無限 × 可算個無限)とかしても
まだまだ追いつきません。
可算個無限をいくら足しても掛けても可算個無限の大きさでしかないんです。
釈迦の手のひらです。
(これは[0〜1]の線分の間にはほとんどが無理数(分数では書き表せない数)が詰まっていて
有理数(分数)を全部集めてもスカスカでしかありませんと言うことでもあります。)
どうやったら非可算個無限無限に到達できるか
それは冪(べき)集合と言う物を使います。
冪集合とは集合内の要素の全ての組み合わせを列挙した物で具体的例を挙げると
冪{1,2,3,4}={ {1}, {2}, {3}, {4}, {1,2}, {1,3}, {1,4}, {2,3}, {2,4}, {3,4}, {1,2,3}, {1,2,4}, {1,3,4}, {1,2,3,4}、{ }}
です。
漢字が難しいので厄介なイメージ受けますが
一般的に言ってyxの事だと思ってまあいいです。
あっ、これなら見覚えありますね。
実際右辺には1、2、3、4の全ての取り合わせ、24の数の要素が現れているのがわかりますでしょうか。
これが冪集合の取り方です。
n個の要素を持つ集合の冪集合は2nの個数を持ちます。
これを自然数全体の集合に適応して
冪{可算個無限}=冪{1,2,3,4,5,6,・・・・}=非可算個無限
を行って初めて非可算個無限に出会えます。(カントールの対角線論法はこれと同じ事です)
計算式で書くと
非可算個無限=2可算個無限
と言う式になり冪集合こそが可算個無限を超え非可算個無限にたどり着く唯一無二の方法です。
2の部分はどうでもいいです。重要なのは冪を取る事で
2可算個無限=3可算個無限=10可算個無限=可算個無限可算個無限=非可算個無限
など元が2より大きく可算個無限以下なら何をとっても結果は同じになります。
可算個無限を越えたスーパー無限、非可算個無限の存在が立証されると
では、「非可算個無限よりさらに大きな無限はあるのか?」と思うのも自然だと思いますが、^^;
・・・・あるんですねこれが。(^^;;;;
もういっちょ冪演算を非可算個無限にかけ、
冪{非可算個無限}
と言う物を作るとカントールの対角線論法により「1:1対応の後に余り」が出てきて
冪{非可算個集合}>非可算個集合
が証明され非可算個無限をも越えたスーパースーパー無限、スーパー非可算個無限が出現します。
でわでわ、「スーパー非可算個無限(冪{非可算個無限})よりさらに大きな集合はあるのか?」は
また冪を取れば
冪{冪{非可算個無限}}>冪{非可算個無限}
でスーパー非可算個無限を越えたスーパースーパースーパー無限、スーパー無限3の出現です。
カントールは無限のランクを表すのにアレフ
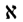
と言う文字を使いました。
ヘブライ文字のAです。無限の序列の発見は数学の中でも大変特別な驚きと意味を持って特殊な文字が与えられました。
可算個無限の大きさはアレフ0と呼ばれます。
しかしこの文字はかなり書きづらいのと、集合論の研究が進み
現代数学の中では無限でさえも普通に扱えるようになると
昔のような神秘性はなくなりもはやただの変数と化したため文字アレフは使われなくなりました。(涙)
今は代わりにω(オメガ)0などと記述するのが一般的です。
いかんせんアレフは一般的なPCの文字コード表じゃ扱いづらすぎるのでここでもωを使いましょう。
まとめると
ω0 =可算個無限(自然数の個数)
ω1 =冪{ω0}=冪{可算個無限}=非可算個無限(全ての数の個数)
ω2 =冪{ω1}=冪{冪{可算個無限}} (これ以降は実世界レベルでは相当例なし。)
ω3 =冪{ω2}=冪{冪{冪{可算個無限}}}
ω4 =冪{ω3}=冪{冪{冪{冪{可算個無限}}}}
・・・・
のように無限を越えた無限を越えた無限を越えた無限を・・・・と果てしなく無限の序列は続くのです。
前章へ 次章へ
最新の日記へ