ぼやき

無限にも大きさのランクがある！3（2009/01/01)

カントールは自身の発見した1：1対応の考えを押し進め
研究を進めると数の世界には面白い構造がある事がわかりました。

カントールによれば
自然数の大きさ（1～∞）
＝偶数の大きさ（2～∞。偶数飛び飛び）
＝整数の大きさ（-∞～∞。整数。）
＝有理数の大きさ（全ての分数の形＝-∞/∞～∞/∞。分子と分母は整数。）
が証明されました。

特に最後の分数なんかかなりビックリです。

例えば[0～1]の間には自然数だと「0、1」の二個しかないのに対して分数だと
「0、1、1/2、1/3、2/3、1/4、3/4、1/5、2/5、3/5、4/5・・・・」とか無限にあります。
この時点で2vs∞ですからそれこそ分数の方が自然数より圧倒的に個数が多そうに
見えますが両者のサイズは同じなんです。

なぜなら
　A＝｛ 1 、 2 、　3 、　4 、　5 、　6 、　7 、　8 、　9 、　10 、・・・・｝　　　 ↑　　↑　　↑　　↑　　↑　　↑　　↑　　↑　　↑　　 ↑ 　　　 ↓　　↓　　↓　　↓　　↓　　↓　　↓　　↓　　↓　　 ↓ 　B＝｛0/0、+1/1、-1/1、-2/1、+2/1、+1/2、-1/2、-3/2、-3/1、+1/3、・・・・｝ このように全ての整数と全ての分数の1：1関係があり、どちらにも余りはでない。を
カントールが明示的に構築してみせたからです。

図にすると下記のように横軸を分母、縦軸を分子として格子状に存在している全ての分数を
巻き取り線でつないだものです。（0除算はスキップ。また通分により既存の点と重複するケースもスキップ）

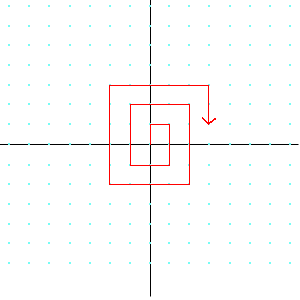
もし分数の方が大きいと主張するならやはり
どちらかの個数が大きいとすれば、1：1対応の後に大きい方に余りが出る
から分数側の余りを明示的に構築し示さなければいけませんが
この通り全ての分数に対して整数のマッチング相手がいますから余りはどこにも出ません。
（巻き取り線から逃れる点はありません）

数学的にはこのサイズの無限は可算個(カウンタブル、countable)無限と呼ばれます。
自然数の個数と同じサイズを持ちます。
全ての要素に番号1、2、3、4、・・・をつけて列挙する事が出来るのと同値です。

ここまで可算個無限を見てきましたが
それでは何が可算個無限ではないかと言うと例としては実数の数です。

実数とは-∞から＋∞にある全ての数です。
具体的には、1、2、3、3.1、1/3、√2、πなど・・・
一切の制限を取っ払った-∞から＋∞の間にある使える限りのありったけの数です。

この実数の総数は可算無限より大きいんです。
背理法で証明してみましょう。

もし仮に、実数の数が可算個無限と同サイズであるとすれば
それらに1、2、3、4、・・・と番号をつけ全てを列挙する事ができるはずです。
すなわち
n₁ = 1.000000000・・・・
n₂ = 2.000000000・・・・
n₃ = 3.000000000・・・・
n₄ = 3.100000000・・・・
n₅ = 0.333333333・・・・
n₆ = 0.141421366・・・・
n₇ = 3.141592653・・・・
・・・・・・・・・・・・・・・・
こんな感じで全ての数に番号がつき、全ての数が列挙でき、全ての数はこの中のどこかに現れるはずです。

しかしここで意地悪して、新しい数であるmを
m＝　小数点1桁目はn₁とは違う数、小数点2桁目はn₂とは違う数、3桁目はn₃とは違う数、4桁目はn₄と、・・・・
として構築します。
これをカントールの対角線論法と呼びます。

mの作り方は何通りでもあるのですが、一つの例として言われた場所を＋1する事で変えて行ったら（9の次は0とする）
この例ではm = 0.1111427・・・・
みたいな感じになります。

さてこのmはn_iの何番でしょうか。

少なくとも小数点1桁目がn₁とは違うのでn₁とは違います。
小数点2桁目がn₂とは違うのでn₂とは違います。
小数点3桁目がn₃とは違うのでn₃とは違います。
小数点4桁目がn₄とは違うのでn₄とは違います。
・・・・・

あらら。困った事になりましたね。
mはどのn_iとも違うので少なくともこの列の中には存在しません。

さっき全ての数に番号がつき、全ての数が列挙でき、全ての数はこの中のどこかに現れるはずです。と言ったのに
列挙できてない数が現れちゃいました。
これは・・・・？

はい、これが無限を越えた瞬間です。
可算無限個な名札を用意しただけでは列挙しきれない、
可算（自然数の個数）よりも大きな無限のランク。
数えられないので非可算個（アンカウンタブル、uncountable）無限と呼ばれます。

またなんとも変な話ですが・・（汗）
やはりカントールのこの論法には他の数学者達が矛盾や反論を出す事ができなかったため
「非可算個無限の存在」、及び「非可算個無限の大きさ　＞　可算個無限の大きさ」
は認めざるを得ないことになりました。
かくして無限のランクは発見されたのです。

前章へ　次章へ