ポアンカレ予想 世界一周してロープを回収できる図形は、球のみか? 14/15
例えをわかりやすくする為に
2次元図形&3次元球表面を使っていましたが
本当のポアンカレ予想は
3次元図形&4次元球表面についての問題です。
(2、3次元と5〜次元については先に証明されて
最後に残った難問が4次元)
ポアンカレ予想:
「単連結な三次元閉多様体は、三次元球面と位相同型であるか?」
これはよく
「宇宙で同じ方向に進み続けて一周して、ロープを回収できたら、宇宙は4次元球の表面と同一であるか?」
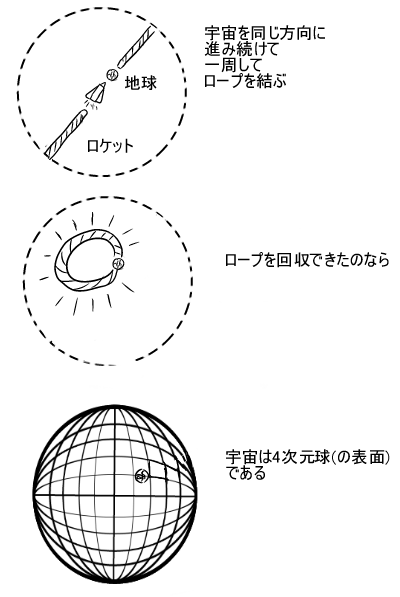
に例えられますがその通りです。
まず
「宇宙で同じ方向に進み続けて一周する」の意味がよくわからないかも知れませんが^^A;
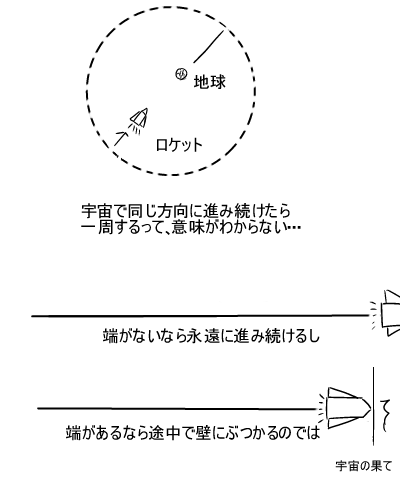
これは地球が
「ローカル視点で見ると2次元だが、全体としては3次元の球体の表面であり、同じ方向に進み続けると一周して戻ってくる」
のと全く同じ原理です。
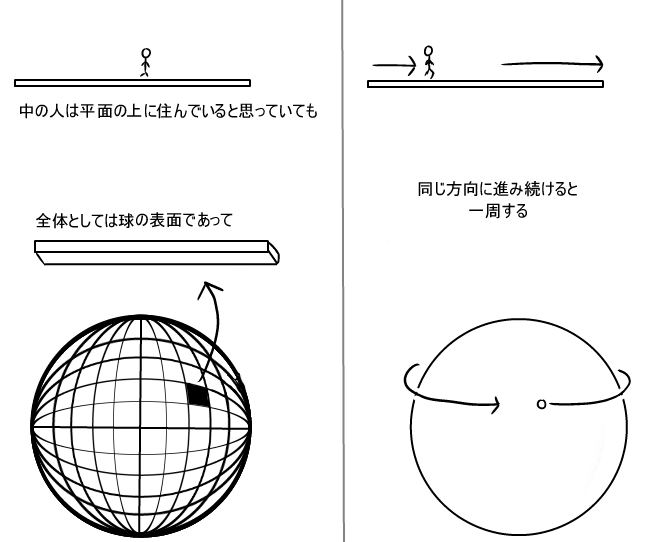
宇宙も
「ローカル視点で見ると3次元だが、全体としては4次元の球体の表面であり、同じ方向に進み続けると一周して戻ってくる」
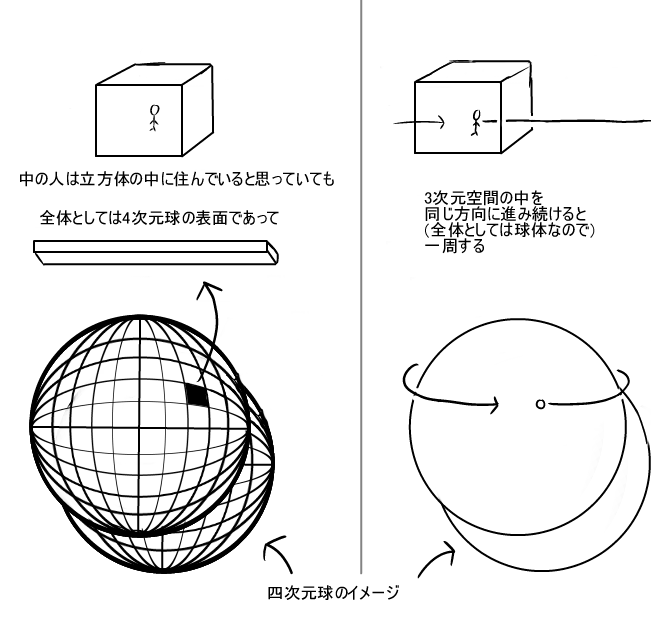
なのです。
ですから
3次元宇宙の中でロケットを真っ直ぐに飛ばし続けると、(4次元球体の表面を)一周して元の地点に戻ってくる
と言うのは実は大アリ。
実際に起っても全くおかしくない現象なんです。
(あくまで理論的可能性ですので、物理学方面からのビッグバン理論などはさておき・・・)
我々の住む3次元世界の宇宙の形には:
・端のある3次元宇宙
・端のない3次元宇宙
・4次元球体の表面宇宙
・4次元トーラスの表面宇宙
・4次元射影空間宇宙
・サーストン分類による残りの5種類基本形
のいずれかが成立します。
が、人類には3次元のローカル座標でしか物事を観測する術がありませんので、
ローカルから全体の形を知るためには
宇宙を一周するロープをたらし、回収できるかどうかで分類すれば
宇宙の形がわかると言うことが
ポアンカレ予想から導かれます。
前ページ 次ページ
トップへ



