ポアンカレ予想 世界一周してロープを回収できる図形は、球のみか? 12/15
リッチフロー理論によって全ての図形を
鍋で煮て
正規化すれば
うまく行くと思われたのですが、
この手法は途中で詰まってしまったのですねー。
例えば図形にこのような結び目がある時に
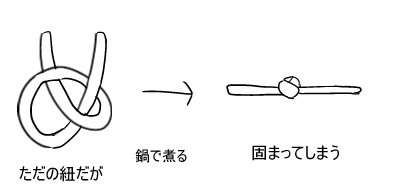
熱を加えると
物体が悪い形で萎縮して、結び目がよりタイトになって
基本形にならないケースが見つかったのです。
注)あくまで例えですよー。^^;
実際には「特異点」と呼ばれる、
ゼロ除算のような非常に厄介な性質を持つ図形で
とてつもなく難しい。
そういう結び目にのある図形に対しては
リッチフロー理論による変形が使えず、
ポアンカレ予想に対する前進が頓挫し20年ほど止まってました。
ここで最後の人、ペリルマンの登場です。
彼は煮詰まった図形を眺め

結び目が絡まってしまったら、
絡まる前まで時間を巻き戻し、
一度解いてから、
もう一度煮詰める、
と、やり直しを提案しました。
注)あくまで例えですよー。^^;;
実際には
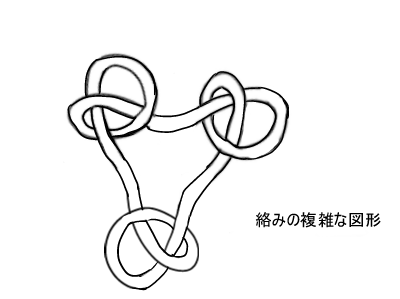
このように絡みの中に絡みの中に絡みがループしてるような
どこからどう始めていいかわからないようなケースもありますので。
彼はリッチフロー理論から生じる「結び目による解かしロック」を分類し、
おのおのを冷静に分析し、
全てのケースで「ほどけないほど深刻な欠点ではない」事を発見し
「時間巻き戻し」&「ほどき」手術によって
結び目ロックをなくせる事を示しました。
こうして
・リッチフローによる鍋煮詰め、
→結び目が生じたらペリルマン手術による結び目ロックの除去
→リッチフローによる鍋煮詰め、
→結び目が生じたらペリルマン手術による結び目ロックの除去
→リッチフローによる鍋煮詰め、
・・・
を繰り返す事で最後には
サーストンの基本8種類図形に還元できる事がわかったのです。
以上3人の成果により
どんな図形でも
基本の8種類図形まで分解する手法が確立されました。
前ページ 次ページ
トップへ


