数とは何か。数学V宇宙の脊髄を自然数が走る。 第5章
Vは数学の中で体現できる全ての物体が入ったいわゆる宇宙です。
一番底は空集合の1点から始り、
そのあと2nのスケールで膨張してゆく漏斗型の世界。
自然数N={{},
{{}},
{{{}}},
{{},{{}}},
{{{{}}}},
{{},{{{}}}},
{{{}},{{{}}}},
{{},{{}},{{{}}}},・・・・}
はその中の一部分です。
Nのn階層のメンバーにはn人しかいないので
2nの速さで増えてゆくVとは
比べものにならない小さな小さな世界です。
しかし、NはVの何に相当するかと言うと中心線・柱なんです。
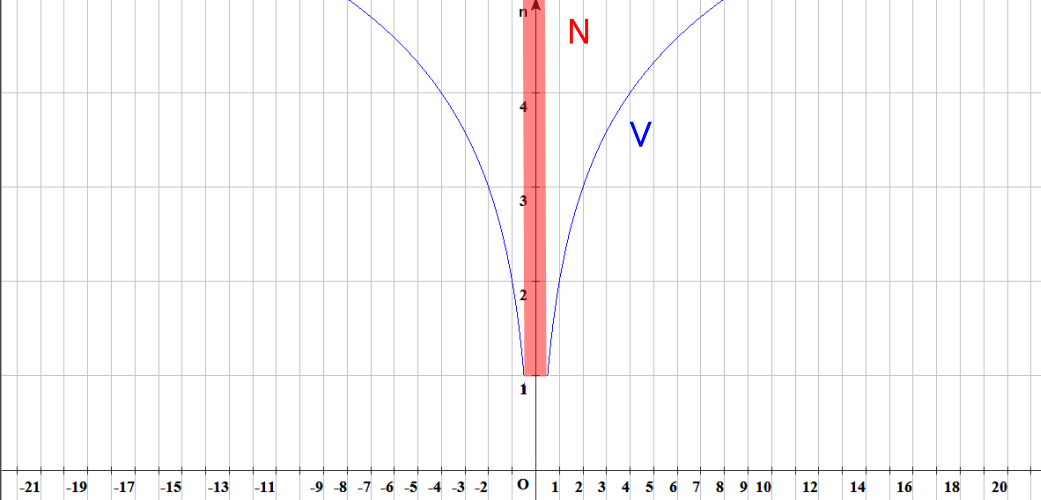
もう一度書きますがNは帰納法で構築すると
1.N1 = {}
2.Nn = Nn-1 ∪ {Nn-1}
3.N = N∞
このように空集合から始まって次々と箱を被せて拡張して
各層で一個ずつメンバーを拾ってゆく柱になる。
ちょっと文学的な表現を許して貰えばNはVの脊髄と言えるでしょう。
『数学』と言う言葉にはいくぶん語弊があります。
大昔は(日本語で表記すれば)名前通りの『数に関する学問』で
ひたすら数に対する考察ばかりだったのでしょうが
現代数学においては
方程式・微分積分・群論・測度論・解析論....などジャンルが数百にまで広がりすぎて
もはや純粋に「数」に関する研究は整数論などほんの一部分ですね。
数学の全ては最終的には集合論へたどり着くので
正確には
「数学とは、集合論から派生した様々なジャンルに対する考察を行う学問」
「数学とは、集合と公理の組み合わせによって生じる問題に対する考察を行う学問」
などと呼ぶべきでしょう。
しかししかししかし!
・数学は最初は数を研究する学問から始まり、
→それから数千年の研究を経て近代数学になると
方程式・微分積分・群論・測度論・解析論・・・の研究が主になり
数は隅に追いやられる。
→ある時から数学の根幹を研究するメタ数学、集合論が始まり
集合論こそが方程式・微分積分・群論・測度論・解析論・・・の基礎だとわかった。
→そして集合論を研究すると
数学はV世界の中の出来事だと発見され
→さらに研究するとV世界の中心には数の柱Nがあった。
歴史の中で最初は主役、それから隅に追いやられたはずの数が
実は数学宇宙Vの中心で人類の到達を待っていたなんて
信じられないようですが本当の話。
数 → 方程式&その他 → 集合論 → 数学宇宙Vの中心が数N
・・・・ロマンチックではありませんか?
前ページへ
トップへ
