測度論と、面積が測定できない不思議な図形の話
「測度論と、面積が測定できない不思議な図形の話(2008/01/03)」
測度論の話をします。
測度論とは何か。
読んで字のごとし、簡単には面積を測る方法を研究する数学のジャンルと思ってください。
英語ではmeasure theory。
多分これだけ聞いてパッ思う所は「えっ?面積を測る研究って何。意味がわからない。」だと思います。
何しろ長方形や三角形の面積を計ることなら小学校から習っていますので
当たり前中の当たり前。
いまさらそんな物の研究と言われてもいったい何を研究してるのかわからないと思います。
しかし話を進めれば面積とは何かと言う命題は通常知っていた常識の中での概念よりもすごく奥深く、
実に面白い話題だと言うのがわかると思います。
少々長くなりますが測度論について興味が出きたならおつきあいください。
まずはおさらいから。
例えばここに一辺の長さが1の正方形があります。
さてこの物体の面積は何でしょうか。
はい答えはもちろん幅×高さで1x1=1。
間違いありません。
ではこちらの三角形の面積は。
答えは幅×高さ÷2で(1x1)/2=1/2。
これも間違いありません。
ここまでは小学校の算数です。
それでは次にもっと複雑な図形に行ってみましょう。
さてこの関数 y = x2 下の緑色の図形の面積はいくつでしょうか。
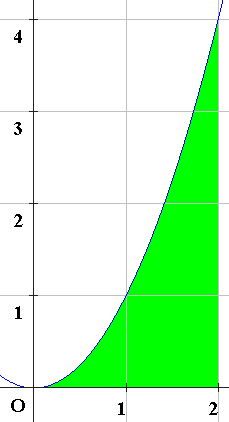
だいぶ複雑になりました。積分を勉強してやっと解けるようになります。
そもそも積分の基本的な考え方とは図形を小さな長方形で挟み込む事にあります。
面積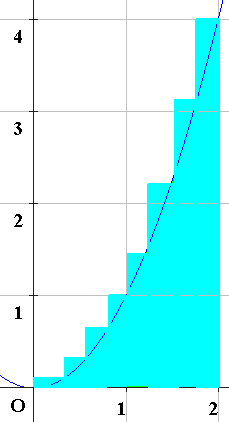 > 面積
> 面積 > 面積
> 面積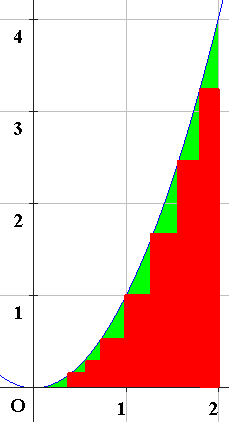
このように「図形を完全に囲う四角形」> 図形 > 「図形に完全に囲まれている四角形」で考えると
図形の面積はその中間になり、後は四角形をどんどん小さくして誤差を少なくしてゆけば
いくらでも細かく図形の面積を測定でき、そして最後には一つのリミットに到達しそれが面積です
計算しちゃうと答えは緑の面積=∫20 x2 = (x3/3)|20 = 8/3
高校の数学です。この積分を正確にはリーマン積分と呼びます。
リーマン積分の発明により世の中の全ての図形は面積を測れるようになった。
ばんざーい・・・・!
・・・・・・
・・・・
・・
・
・
と昔は思われていたんですが実はその後の研究により
リーマン積分じゃ面積の測れないとんでもない図形が存在する事がわかったんです。
「病的」とも呼ばれる恐ろしくひねくれた、しかし理論上は確かに存在する困った図形。
今までの理論がまるで通用しない化け物を目の当たりにした数学者が
改めて「じゃあ面積って何だ。長さって何だ。測るって何だ。」を考察する必要にぶつかり
測度論は生まれました。
その面積の測れない図形とは何でしょうか。
説明自体はさほど難しくありませんので今この場で具体的に示します。
関数f(x)を以下のように定義します。
{ 1 もしxが有理数なら。
f(x) = {
{ 0 それ以外(xが無理数)なら
(このタイプの関数の書き方はあまり見慣れないかも知れませんが
関数とはそもそも「x→y」のマッピングそのものであり、「xがわかればyが確定できる」が関数の定義です。
このf(x)はその定義を間違いなく満たすのでれっきとした関数でありここに問題は何もありません。)
有理数とは数学用語で分数の事です。
例えば1/2、1/3、3/5、121/25・・・・分数ならなんでも。
無理数とは有理数ではない数の事です。
具体的には√2など。√2はどんなに桁の大きい分数を持ってきても表現できない数です。
その他にも√(素数)は全部無理数ですし、有名なπやらeなどの定数も無理数です。他にもいくらでもあります。
他の言い方をすると、
小数点で書いたときに有理数は桁の繰り返しパターンが必ず発生します。
1/1=1.00000000000000・・・ (0の繰り返し)
1/3=0.33333333333333・・・ (3の繰り返し)
1/7=0.14286714286714・・・(142867の繰り返し)
・・・
無理数は繰り返しパターンが発生せず永遠に新しい数字が出てくる物です。
√2 = 0.1414213562・・・
π=3.141592654・・・・
・・・
前述の関数のグラフを書いてみましょうか。どうなるか。
それがこれ!
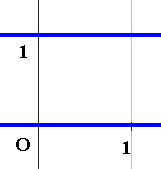
・・・・・あらら(^^;
変な事になってますね。
y=0の所とy=1の所に2本の線があります。
実際は2本あるわけじゃありません。
もっと拡大してみると
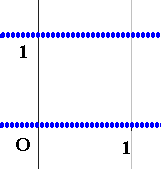
このように上下の線ともこのような細かい点々によって構成されている点線なのです。
しかもただ細かいわけではなく、上下ともに細かさは無限に細かい
逆に言うと密度が無限に高い超点線です。
なぜなら0〜1の間には1/2、1/3、2/3、1/4、3/4、1/5、2/5・・・・1857455468943275940325/3657455468943275940325・・・・
のように無限に細かい粒子度で無限の有理数点が存在し、
また無理数の方でも0〜1の間には0.49021840321975890427590423785942375・・・・・
といくらでも細かい粒子度で無限の無理数点が存在しているからです。
上下の点線とも点線ながら実際は果てしなく濃く、しかし絶対に連続点ではなく確実に分断されている点の集まりです。
問題はこの関数の、x=0〜1の間にある領域の面積になります。
これは何でしょう。
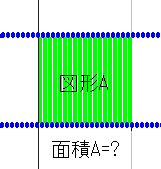
緑の一個一個自体は高さ1の短冊の寄せ集めとなります。
しかしただの短冊じゃありません。点線が無限の細かい超点線であったように
短冊の幅も無限の細かい超短冊で、実際にそれぞれの短冊の幅はそれに対応する有理数点の長さと同じ長さ、すなわち0です。
これがリーマン積分では測定のできない異常な図形です。
なぜならリーマン積分は「図形を完全に囲う四角形」> 図形 > 「図形に完全に囲まれている四角形」になるよう細かい四角形を持って近似しますが
この関数に対しては上限はy=1の無限に細かい点線であるため
上限四角形を取ろうとするとどれだけ細かい四角形を用意しようとも
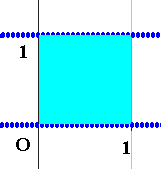
このような1x1の四角形になります。
なぜなら上限を狭めようと思ったら青領域の
1.高さを低くする
2.幅を小さくする
の2通りの方法がありますが、1.は上の点線の高さが1なのでそれを囲う必要があり1未満にはできないのでまず却下。
2.は途中の区間をどこか間引いて面積を減らそうとしても
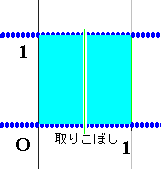
緑短冊は無限の細かさでx=0〜1のいたる所に存在しているため
どこをどれだけの細かい幅で抜いても
必ずどれかの緑の短冊の取りこぼしが発生するので減らすわけにはいきません。
結局高さも幅もこれ以上は減らせず、上限は1x1の四角形になります。
同様に下限を取ろうとするとどれだけ細かい四角形を用意しようとも
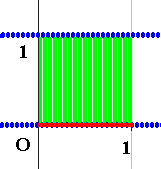
このような0x1の四角形になります。
これ以上下限をあげようと思うとどこかの緑短冊とぶつかるので上げられません。
よってどれだけ細かい四角形を用いろうとも上限=1 > 図形 > 下限=0で
これ以上は緑短冊の面積が挟み込めません。
無限に細かい短冊で構成される超物質は
リーマン積分の限界を超えた細かさのせいで面積を測る事ができないのです。
これが面積の測れない図形の1例です。
0と1の間にある事は間違いないのですがそれ以上がわからなく、実質的に「測定不能」状態に陥ります。
このような通常の意味では面積を測れない異常な図形の存在が示された事はものすごい衝撃がありました。
なぜって、今までみんながリーマン積分を面積を測るための「物差し」として当たり前のように使っていたのに、
その物差しの通じない事例が現れたのです。
物差しが通じないと、その「物差し」自体の信憑性に疑問が向けられるようになって
「物差しの目盛りが正しい保証はどこにあるのか?」
「この物差しでいいのか?」
「もしかして今までの計測も全部間違ってたかもしれない」
と今までの計測行為全部が疑わしくなってきます。
わかってるようで誰もわかってなかった。
面積って何なんだろう。どうやったら測れるんだろう。
そこで「いかなる集合(図形)の面積でも正しく測り、そしてその計測が正しい事の根拠を与える」ための理論、
それこそが測度論が誕生した理由です。
その後数学界はこの問題にどんな答えを出したか。
結論から言っちゃうとルベーグによって発明されたルベーグ積分が答えを出しました。
答えは0です。この緑短冊の面積は0であるとするなら納得がゆき、逆に0以外の数では矛盾が起こる、
よって0であると結論づけるのが妥当であるとの判決がでました。
0だったのです!
よかったよかった。これで安心して眠れる。zzz
・・・・
・・
・
が、しかし、その後の研究によりなんとルベーグ積分でもまだ面積の測れないさらに異常な超図形が発見されてしまいました。(^^;
数学者たちは再度「じゃあ面積って何だ。長さって何だ。測るって何だ。」の旅へと。
そして測度論は一つの結論に辿り着いた・・・
ルベーグ積分とは何か、どうやって計算するか。そこら辺を近日中の次回に書きます。
次章へ
最新の日記へ



 > 面積
> 面積 > 面積
> 面積





