測度論と、面積が測定できない不思議な図形の話 - 2
前回は視覚的にわかりやすい例として二次元の図形を用いて測量不可な面積の話をしましたが
物事を単純にするためにこの章からは問題を1次元にして話を進めます。
すなわち「面積とは何か」の前に「長さとは何か」を議論します。
面積＝長さ×長さ ですので。
長さを知らないことには面積を語れないですし
長さがわかれば面積も自然と出てくるわけです。
まずはx=0〜x=0の線分を考えます。
図8.1
この線分の長さは何でしょうか。
答えは0です。線分と言ってもただの点ですから。
次にx=0〜x=1の線分を考えます。
図8.2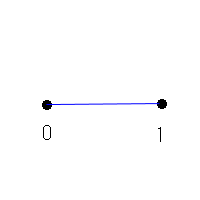
この線分の長さは何でしょうか。
答えは1です。0〜1をフルに埋める完全線ですから答えはストレートに1。
ここまでは問題ないと思います。と言うか当たり前すぎて他に答えがあり得ません。(^^;
ややこしくなってくるのが次から。
図8.2の線分からx=0.5の1点だけを取り除きます。
図8.3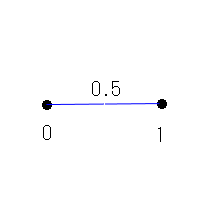
この線分の長さは何でしょうか。
答えは1です。
なぜなら点の長さは0なので、線分から1点を取り除いた所で
長さは1-0=1で変化しないからです。
じゃあ図8.3の線分からx=0.01、0.02、0.03、・・・0.99まで100点を取り除くと長さはいくつでしょうか。
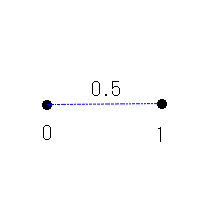
答えは1です。
なぜなら点の長さは0なので、線分から100点を取り除いた所で
長さは1 - 0x100=1で変化しないからです。
同じ原理で線分の中から点を1億個、100億個、1兆個、1000兆個・・・どれだけ大きい数だけ取り除いた所で長さは変化しません。
長さ0の点がいくら集まった所で長さは0なのです。
逆の言い方をすれば、線はまさしく無限の超超超超超超多数の点から構成されてますので線の中から
高々1000兆程度の点を取り除いた所で線の長さに影響は全くないのです。
数学的に正確に申しますと可算個（カウンタブル）と言う単位までの数は取り除いてOKです。
可算個の範囲でいる限りはどれだけ点を取り除こうと長さに変化は起きません。
可算個の反対は非可算個（アンカウンタブル）と呼ばれる可算個よりもサイズの大きい単位で、
非可算個の点を取り除く段階で始めて長さが変化します。
ここの可算個、非可算個は完全に専門の話になって一つの数学ジャンルになるので
この場での説明は難しいですが
具体例を挙げると有理数の数は可算個、無理数の数は非可算個である事は証明されています。
よって長さ1の線分から全ての有理数点を取り除いても長さは変化しません。
1のままです。
終わり。
なんだかよくわからないかも知れませんがあまりにも難解で
これ以上の説明はこの場ではどうしてもできません。
そういう物だと思って納得してください。すいません。
さてここに目をつけたのがルベーグで、
要するにルベーグが提唱したのは「線分の中から可算個までの点を取り除いた所で長さは変化しないとする」
と言う予測をうち立て、
そしてそれを元に理論を展開し初志の「線分の中から可算個までの点を取り除いた所で長さは変化しない」ルールを守る限りは
その後どこにも矛盾が発生しない事を厳密に証明しました。
ルベーグ測度の誕生です。
そしてルベーグ測度をもって長さ・面積・体積・・・を測るのがルベーグ積分です。
ここからちょっと具体的なルベーグ測度の定義を書いてゆきます。
数式に書くとこう。
集合Aに対するルベーグ外測度（長さ）とは
m*(A)=inf{Σ|Ij|:Ijは開区間でA⊂∪Ijなるもの}。
を持って定義される。
infはinfimumの事で「最小の」の意味です。（紛らわしいですが無限のinfinityとは全く関係ありません。）
開区間とはa〜bまでの2点間の全ての点の集合（ただしaとbの2点だけは含まない）
要するに端っこ2点の消失した線の事です。
⊂は「含む」と読みます。
∪はIj全てのor集合です。
わかりやすく日本語に読み替えると
「あらゆる開区間の組み合わせでAを囲む事をトライし、そして結果その中で最小の合計の長さを持った開区間群の長さの合計を、集合Aの長さとする」と
定義されてるわけです。
ちなみに前節の「開区間群の長さの合計を、集合Aの長さとする」の部分、
「長さを定義するのに、長さを使ってるじゃん？それっておかしいじゃん？」と思われるかも知れませんが
開区間(a,b)の長さはb-aとして定義で確定しますので問題ありません。
開区間とは言ってみれば物差しです。
ルベーグ外測度は「物差しじゃ普通測れないような不可解な図形の長さ」を物差しで測れるようにするための測量の方法論を提示しようと言っているのであって、
物差し自体の長さは測量せずとも確定しています。それぐらいはないと本当にどうしようもないですから。（汗）
何言ってるかさっぱりわからなくても安心してください。それが普通です。(^^;;;
わかりやすく図解してみましょう。
ここに0〜1の線分があります。
図9.0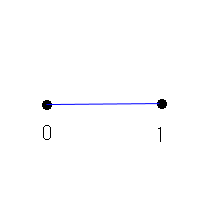
この物体のルベーグ長さを測りたいとします。
すると次の手順に、複数の物差しを用いてこの物体を外側から囲う組み合わせを考えます。
組み合わせには多数あります。
例を挙げますと
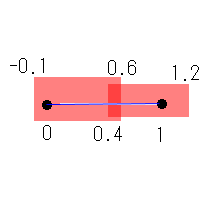
（-0.1〜0.6）＋（0.4〜1.2）の二つの領域を用いて(0.0〜1.0)の範囲を囲ってみました。
この場合の長さは線分(0.0〜1.0)を覆う二つの四角形（-0.1〜0.6）・（0.4〜1.2）の長さの合計、
すなわち0.7＋0.8＝1.5になります。
(0.0〜1.0)をかなりオーバーしてしまいましたが多めに見積もる分には構いません。
重要なのは(0〜1)が完全に囲まれている事で。
他はこんな
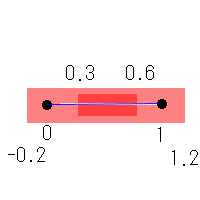
恐ろしく効率悪いどころか空回りしてますが(0.0〜1.0)を囲っているのでこれも一つの立派な囲い方です。
この場合の長さは1.4＋0.3＝1.7。
一番効率がいい方法としては
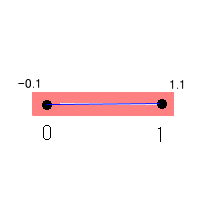
このように（-0.1〜1.1）の開区間で囲って長さを1.2とし、
次に（-0.01〜1.01）の開区間で囲って長さ1.02、
次に（-0.001〜1.001）の開区間で囲って長さ1.002、
・・・・
で最後には
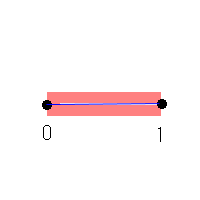
（-0.000000000....1〜1.00000000000....1）の開区間で囲って長さ1.0000000000.........。
すなわち1.0に極限で持ってくる方法です。
これが「ありとあらゆる組み合わせの囲い方を考える」と言う意味です。
そしてその中で一番長さの少なかった物を探します。
今回の例だと最後の囲い手法で見つかった長さ1.000000000000.......が最小ですから、それを持って「線分(0〜1)の最小の長さは1.0である（っぽい。今の所は）」
と宣言します。
無論今回たった数件の囲み方リサーチで終わらせたのはプロセスをわかりやすく解説するためです。
本当なら、数学的に(0〜1)を囲う事のできる四角形の組み合わせの無限のパターンを試行し、
そしてその中で最小の物を選ぶのです。
このあと似たような物にルベーグ内測度もあってルベーグ内測度も同様に測って、
そしてルベーグ外測度＝ルベーグ内測度が一致し集合はルベーグ可測である事が確認されて
やっと長さが確定します。
これがルベーグ測度の測り方です。
さてなんでこんな変で滅茶苦茶わかりづらいような定義の仕方をしているかと言うと(^-^;;
そもそもリーマン積分で困ったのは前章のような「どうやって面積を測ったらいいかすらわからない！」とてつもなく不可解な図形が見つかったからで、
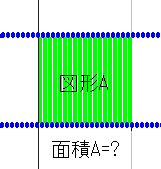面積の測れないとてつもない図形
その解決策としてルベーグは「だったら、あらゆる角度・あらゆる場所・あらゆる長さの物差しの組み合わせを全て試し、その中で最小になった四角形囲いの面積の合計を、不可解図形の面積として選ぼう。」
と提唱したわけです。
「測り方がわからないなら、とにかく全部試せ！」
一見無責任で荒唐無稽で酔っぱらいのような話ですが(^^;;
実際理論的に検証してみるとわかるのですがこれがうまくいくんですね。
そこに目をつけたルベーグの先見の明はすごいです。
この「開区間の総当たりでとにかく測れ」論法がルベーグ測量の礎にあり、
それを持って導かれた結論の一つが前半の「可算個までの点を取り除いても長さは変化しない」になるわけです。
いかがでしたでしょうが。
ルベーグ積分は面積を「ルベーグ長さ幅×高さ」で測る物と思っていいです。
そしてルベーグ積分は：
・リーマン積分が行える図形に対しては「ルベーグ積分面積＝リーマン積分面積」を満たし、
・リーマン積分が行えない図形に対しても面積を測る事ができるケースがある（できない図形もある）。
リーマン積分を拡張してより多くの物体の面積を測れるようにした一歩進んだ積分法といえます。
今まではただ漠然と「長さ・面積」の概念があるだけで誰も本当の意味を考えもしませんでしたが
ルベーグのアプローチにより「長さ・面積」とは何なのかをちゃんと研究・発展できる事を示されました。
次回は「長さ・面積」とは何かを語りたいと思います。
測量の方法論についての議論は難しいですが実はこれだけなら結構簡単。
我々が「長さ・面積」について持つ概念から要請される「長さ・面積が、長さ・面積たる条件」だけならものすごくシンプルに説明できるんです。
前章へ 次章へ
最新の日記へ