ぼやき

測度論と、面積が測定できない不思議な図形の話 - 3

これまでに面積の測れない不思議な図形を見てきました（ルベーグ積分によって測れるようになりましたが）。

古典的な方法では全くどう処理していいかわからないような問題を前に数学では自然と
「いったい面積って何？」の疑問が立ち上がったわけです。
そこで常識と照らし合わせて「これが面積だ！」な面積が満たすべき最低限のルールが整備され提示されました。
以下それを説明します。

まず図形Aを入力に取り、そして実数値を出力する関数を面積関数と呼ぶことにします。一般にm(A)と書きます。
そして面積関数mは以下の項目を満たすべきとします。
（わかりやすさの為に本来の数学定義から日常的な用語・用例に変換してます。必要なら図形←→集合、面積←→長さと読み替えてください。）

1．幅a、高さbを持つ長方形の面積はaxbである。

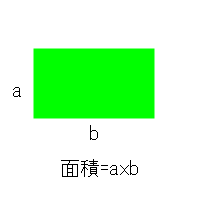
基本長方形の面積は常識的であるべきと言っています。

2．面積は図形の平行に不変である。m(A) = m(A+x)

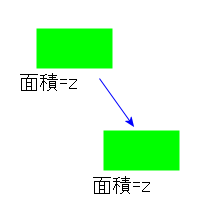
図形を動かしてもその面積は変化しないと言っています。当たり前です。

3．面積は加法性を満たす。m(A+B)=m(A)+m(B)。

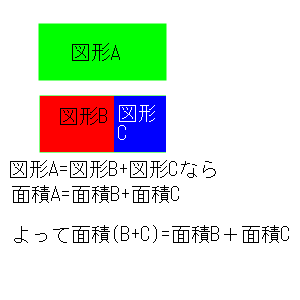
図形をどう分割した所で合計の面積は変化しないと言っています。当たり前です。

そして以上「1）～3）の性質全てを満たす面積関数mによってm(A)=aで計算された非負実数値aをAの面積」と呼ぶ。
これがだいたい数学的な面積の定義です。

どの項目も実に常識的でびっくりするほど当たり前です。
それもそのはず。我々が「面積にはこんな性質があるはずだ」と思っていた事を明確に定義したのが1)～3)ですから。

なお面積の定義は一つではありません。
以上の1）～3）を満たす面積関数mから算出された物は全て「m面積」になるわけで選択は任意にあります。
例としてはリーマン測度によって面積を測って算出された「リーマン面積」に
ルベーグ測度によって測って算出された「ルベーグ面積」など。
選択した面積関数によってその時の面積の意味と○○面積の値は変わります。

そして面積関数の条件の最後が

4（希望）．面積関数mは全ての図形に対して面積を算出する。

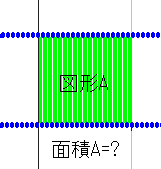
どんな図形でも面積を測る事ができる。

です。

なぜ4．に（希望）の注釈がついているかと言うと
第一章に出てきたような「今までの方法では面積の測れない不可思議な図形」みたいな発見があり
この先のどんな図形にでも面積が測れる事を保証すると言うのは簡単そうに見えて実は大変難しい行為だからです。

テーマは決まりました。
測度論の理想としては1)～4)の性質を満たす究極の面積の測量法を探す事と言っていいでしょう。
これを目標に研究研究～♪

と、思っていた所に・・・・
・・・
・・
・

見つかっちゃったんですね。
1)～3)の性質を面積に要請する限りは絶対に面積を割り当てることのできない超異常な図形が。

どういう事かと言うとある奇妙な図形Xがあって、
その図形Xの面積にはどんな数（0，∞、その中間の普通の数）を割り当てても
矛盾を引き起こす事がわかったのです。

なので図形Xには面積xをつけられない。
結局測量行為そのものを放棄し「図形Xの面積はどこをどうやっても絶対に測れない」として
面積に関する議論から切り捨てるしかない超ド級の病的図形が見つかったのです。

これすなわち測度の希望条件4の「どんな図形の面積でも測れる」は満たせない、
イコール、究極の測度なるものは存在しない事の証明が早々と提出されてしまったのです。

次回はその図形Xを実際に構築します。
Xは有理数と無理数をうま～い事張り合わせて実現した物で
難解な専門用語を使わなくても定義そのものはわりかし簡単にできます。

前章へ　次章へ