1+2+3+・・・・ = -1/12 日記
「CG(2012/05/30)」
今日のCG。オリジナル。4コマショートストーリー。

たまにはちょいしんみりしたお話も。
「購入ソフト予定(2012/05/28)」
最近は世界樹の迷宮4の公式HPに置いてある
BGM 04をよく聞いてます。
FM音源バリバリ。これぞゲーム音楽!って感じ。
作曲は古代祐三さん。
この方の作られた曲の中ではSFCアクトレイザー、町の曲(ノーマルバージョン。捧げ物ではない方)が一番好きです。
さて。ゲームに関しては残念ながらスルー予定です。
他にソフトがなかったら買ってたと思うのですが
いかんせん7月はルーンファクトリー4も出る。
3が良作だったので個人的に楽しみ。
それで世界樹4(発売日:2012/7/05)をもし買ったら、
多分クリアする前に
ルーンファクトリー4(発売日:2012/7/19)が来て
バッティングしてしまうのです。
5月にテリー、6月にポケモンの激戦区を避けた結果
7月に世界樹4&RF4の中堅RPG二つがぶつかっちゃった感じかなあ。困る。(´д`;
評判良かったら後から買うかも知れませんがとりあえずRF4から。
「デッサン人形(2012/05/26)」

ロボット魂 ガンダムAGE-1 スパローを購入。

構図に困ったときのデッサン人形に使おうと思いまして。
なるべく人間体型に近い、かつ可動域が高いと言うことで
この機種を選びました。
同じデッサン目的でガンプラ「RG RX-78-2ガンダム」も

前に買って持っていたのですが
いまいちジョイントが弱くてパーツが取れやすい(汗)
ロボット魂は
ガシャガシャ動かして遊ぶタイプのおもちゃっぽいですし
モデルに使うならそっちの方がいいんじゃないかな?と。
ちなみに両者を触ってみたのですが
可動域・稼働箇所・ディテール・価格など、「耐久性」以外では全てガンプラRGの方がロボット魂より上でした・・・
量産効果でしょうね。おもちゃの中でもガンプラのクオリティは頭一つ飛び抜けてます。
あの価格であの品質は凄い。
「CG(2012/05/24)」
今日のCG。アニメ「戦国コレクション」から塚原卜伝。

2012年春アニメも中盤戦ですがこれがダークホースでした。
・戦国武将が現代にタイムワープして奇妙な装束で闊歩してるのに
街の人が誰一人疑問に思わない世界観
・第1話でやってた話は一時中断、第2話にして新・主人公編が始まった(1話1ヒロインのオムニバス形式だったのですが)
・伏線がうまく回収されたと思いきやもっと重大なシナリオの不具合を平然とスルーしてそのまま話が終わる
・主人公のセリフが一話丸ごと5・7・5で喋る
・等々・・・
前衛的なアニメ!
脚本も毎度超展開してて最初はパニック状態でしたが
1話1話が映画(洋画)のオマージュになってるって気づいてからは
すんなり見れるようになりました。
元ネタと常にセットですね。
オリジナルを知ってないと意味が通じないストーリー・演出になってる。^^;
もしわからなくても(私も半分ぐらいしかわかりません)、
元がどれも名の知れた名作だけあって映像の雰囲気に味がある。
ショート映画な感じに見れば楽しめるかと。
「銀河旋風ブライガー(2012/05/22)」
ロボットアニメのコンピレーションCDをレンタルしてきました。
お目当ては「銀河旋風ブライガー」。

冒頭ナレーションの
夜空の星が輝く影で、悪の笑いがこだまする。
星から星に泣く人の、涙背負って宇宙の始末。
銀河旋風ブライガー、お呼びとあれば即参上! (CV.柴田秀勝)
が渋い!
このアニメは見たことなかったのですが
ニャル子さんのパロで使われてたのから
元ネタ調べて入りました。^^;
「CG(2012/05/19)」
今日のCG。バイオリン少女。

オチつき

そういえば私の絵って女の子が困った顔してるのちょっと多い(´д`;
目の描き方も(平均的な萌え絵と比べて)白目が大きいのは意識してます。いわゆるびっくりした時の瞳の縮小表現がデフォでやや入ってると思います。
別にイヂワルしたいわけじゃないんですが、
オロオロ・赤面してる仕草や表情が可愛くて。
本当に困った事にはならないよう後でオチつけてフォローしたりも。
「世界樹の迷宮 OST(2012/05/18)」

DS「世界樹の迷宮」のサントラを借りてきました。
なつかしー。
これDSで遊んでたんですよ。
ゲームとしては全体的に・・・荒削りでしたね。
ゲームバランスはかなり悪かった記憶があります(^^A;
例えば全く使えない職業・スキルとかが多くて、
キャラクターを間違った方向に育成しちゃうと
まるで役に立たないダメダメ君が出来ちゃう。
はいキャラ放棄〜
そうして使えるスキルを見つけるまでに夥しい数の実験動物が・・・・
なんとかそこを越えてベスト職業・ベストスキル・ベストパーティーを見つけると世界が変わる。
私の場合はソードマン・レンジャー・レンジャー・バード・メディックに落ち着きました。(覚えさせるスキルも調査済み)
この5人、私の編成した「マイ・最強の勇者軍団」でダンジョンを圧倒的有利に
突き進むのが楽しいゲームでした。
音楽に関してはダンジョン1(樹海)、ダンジョン4(枯れた森)、ダンジョン6(遺都シンジュク)が
好きです。
「コンプガチャにおける数学的考察3(2012/05/15)」
ガチャコンプ続報。
GetNewsがアイドルマスターコンプガチャシミュレーターをやってみた。
今回はこちらを解析します。
システム
・1500円で5ガチャ、6回引ける
・特定のカード6枚でコンプ
・カード総枚数不明(X)
・全てのカードは均一に出ると仮定する
シミュレーション結果:
・4万6500コイン(=186ガチャ)で5/6人まで揃った。
・8万8500コイン(=354ガチャ)でコンプ完了
この条件を使い、前回と同じ手法で母集団を推定しますと
X/6+X/5+X/4+X/3+X/2+X/1 = 354
X = 144.5
四捨五入してX=145枚と算出します。
サンプル数としてはやや少なく統計的な信憑性の面では苦しいのは重々承知ですが。
参考記録レベルでいいなら当てられます。
(ドロー354回は回数としてはそこそこあります。
ただ少なくとも被験者「一人」と言うのがサンプル採取エラーを防ぐ意味でマズい。
そもそもソースが本当に正しいか、信頼できるか別の問題が出ますので。)
システム:
・1500円で5ガチャ、6回引ける
・特定のカード6枚でコンプ
総枚数フィードバック後の推定モデル:
・カード総枚数145枚
・全てのカードは均一に出ると仮定
・すなわち、コンプ対象のカードは1/145の確率で出るとする。
(後に書きますが、重要なのは下線部分1/145の箇所です。
ここさえあっていれば計算結果は正しくなるので
実際の総枚数および各カード確率分布とは違っていても構いません。そこはつっこむ所ではありません)
このデータに基づくと
残6→残5までに必要な期待値枚数は145/6=24枚、
残5→残4までに必要な期待値枚数は145/5=29枚、
残4→残3までに必要な期待値枚数は145/4=36枚、
残3→残2までに必要な期待値枚数は145/3=48枚、
残2→残1までに必要な期待値枚数は145/2=73枚、
ラスト1枚を揃えるのに必要な期待値枚数は145/1=145枚、
視覚化すると
残6
(24) | 残5
(29) | 残4
(36) | 残3
(48) | 残2
(73) | ラスト1
(145) |
累計比較:
・理論的期待値
・GetNewsによる実際のドロー
うん、それなりに近いでしょ。
ズレてる分は確率の揺らぎですからここまで近似できてれば上出来。
システムの仮定では
・カード総枚数145枚
・全てのカードは均一に出ると仮定する
がかなり怪しかったのですが・・・実はそこ関係ないんですね。
本物の出没結果に合わせてXを逆算した事で
実際の「カードの総枚数Y、各カードの出現確率にはウェイト付けがある」モデルからガチャを引く状態を
「カード総枚数145枚、全てのカードは均一に出る」モデルからガチャを引く状態で出せるよう
エミュレートしてるわけですから。
コンプに必要な目的カードの出現確率さえ一致してる限り(それは逆算で合わせた)
実際の総枚数、および通常カードの出現確率は関係ないんです。
さて今回のポイントは
ラスト1枚を引くのに必要な労力:ラスト1枚まで持ってくるのに必要な労力
の比率。
理論的期待値:145/210=0.69
実際: 168/186=0.90
一般的なガチャコンプでは
(最後の一枚を引くのに必要な労力) = (最後の一枚まで持ってくるのに必要な労力)×0.5〜1.0
みたいな法則が成り立つのがわかります。(かなりおおざっぱですが)
だから「最後の一枚だから。あともうちょっと・・・」なんて
考えは非常に危険。
まだ全体の半分しか進んでない事を認識してください。
あと問題としては
「サーバーに不正行為(途中までは揃えやすいのに、最後の一枚になると急に出にくくするような出目操作)はあるか?」
がありますが・・・
そこは確率の問題ですから
ユーザー:最後の一枚で急に出にくくなった。不正だ!
運営:運が悪かっただけです。
ユーザー:他にも同じような「最後の一枚で急に出にくくなった」ユーザーがたくさんいる。不正だ!
運営:「最後の一枚がすぐに出た」ユーザーもたくさんいます。抽選は公平です。
などと返されたら非常に反論が難しいです。
(実際に最後の一枚ってのは恐ろしく引きづらい物ですし)
少なくともその場の追求では完全な水掛け論なので無意味。
例えば100人のユーザーがコンプして、コンプまでに出たカード行程全てを納めた表を作るぐらいの
豊富な実サンプルがあるなら文句のつけようがない「統計的に見て異常に偏ってる」の検証も可能ですが。
ちなみに表を作る時にはガチャの画面をネットで生放送でもしながら行ってください。
そうでもしないと
運営:本当にこの出目が出たんですか?あなたに都合良く表を改竄してませんか?
と言われ統計としての価値がなくなります。
しかしまあ。多分表を作り追えた頃には
キャンペーン終了して次のガチャが始まってるでしょう。(汗)
繰り返しますが、
少しでも不満があるなら最初からやらないのが一番です。
ギャンブルってのは必ず胴元有利になるように出来てるんです。
「コンプガチャにおける数学的考察2(2012/05/12)」
前回からの続き。
システムは
・ガチャ1回300円
・カード総枚数50枚
・全てのカードは均一に出ると仮定する
・特定のカード5種類を揃えるとガチャコンプ
とします。
その場合の必要なガチャ期待値はこれ。
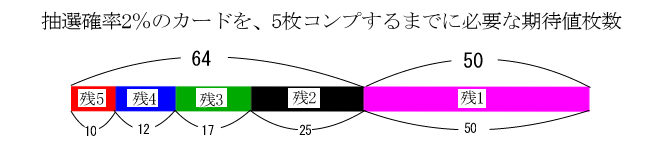
ここで、もしあなたが5枚中4枚コンプリートの状態まで来たとします。
期待値的には64枚のカードをすでに購入、使った金額は64ガチャ=19200円。
悪魔の選択。
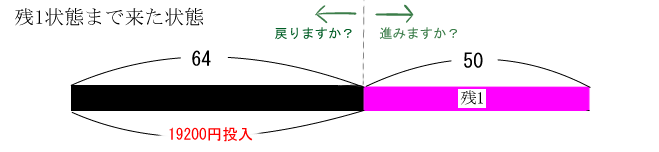
戻りますか?(お金を使いすぎたのでもう止める)
進みますか?(コンプまでお金を注ぎ込み続ける)
仮に戻るとすると
19200円も使っといて、それでいてコンプリートならず。踏んだり蹴ったり。涙目。全く良い所なし。
いままで注ぎ込んだお金は無駄となりまさにドブへ捨てたのと同義になります。
投資:19200円。収穫:なし。純損失:19200円
しかし仮に進むとすると、
追加投資15000円
が必要になります。
19200円も注いだのにさらに金を払うなんて
冷静に考えたらどう考えても損な決断です。orz
が!しかし!
追加投資で一度コンプを成功させてしまえば
投資:19200+15000=34200円。収穫:コンプカード。代金:34200円
使ったお金は「コンプへの代金」と言う形に化けます。これは正当な買い物なので、無駄金ではありません。
これがコンプガチャの怖さ。
途中で止めたケース :収穫なしの、純損失:19200円
コンプまで続けたケース:収穫コンプカードの、代金:34200円
どちらが得なのかは価値観の問題ですからそこを考えるのは全く無意味ですが、
それでも収穫なしの純損失19200円は痛い。
それならいっそトータル34200円払ってでもコンプまで進めて
「今まで注ぎ込んだお金は決して無駄金じゃない」と自分の行為を正当化させねば・・・と
考えても全く不思議ではないです。
別の視点からはこう見ることもできます。
最後の1枚の時点まで来ちゃったら、
後戻りするより、先に進んでコンプを完成させる方が
距離が短くなっちゃうんです。
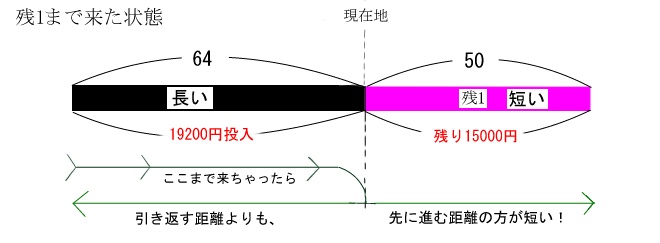
あー、なるほどね・・・
えげつないほどうまくできてます。^^;
コンプガチャを止められないのは理論的にも裏付けする理由があった。
いままでの損失を取り返そうと追加資金を投入して、
その結果膨らんだ損失をさらに取り返そうとまた投入して・・・
沼に嵌る構造としてはギャンブルと全く一緒。
しかも抽選の権利、保障されるべき確率の公平さを
胴元に握られてるんですから勝てるわけない。
(以前にもどこかのMMORPG内で超超超レアアイテムをゲットできたのは運営のサクラなのでは?事件があったと思います。)
結論としては・・・
一番良いのは全くやらない事でしょう。(爆)
損失0円。いままで見た中でもっとも金額的損失を少なくする方法なのは間違いないです。
「コンプガチャにおける数学的考察1(2012/05/11)」
最近なにかと話題のコンプガチャ。
コンプまでにどれだけのガチャが必要かを
数学的に考察してみました。
面倒な理論はスキップして!と言う方の為に
まず結論から言いますと
わかった事は
「最後の1枚の時点で急激に難易度が上がる」
それを視覚化したのが以下のグラフです。

とあるカードコレクションがあったとして、
「特定の5枚をコンプしろ。各々のカードの抽選確率は2%。」と言う条件が出たときには
期待値として114回カードを引く必要があります。
(1ガチャ300円だとして、114ガチャ=約3万円。実物のコンプガチャに必要な金額に近いと思います。)
その内訳として、残5→残4までに必要な期待値枚数が10枚、
残4→残3で12枚、残3→残2で17枚、残2→残1で25枚、最後の1枚をゲットするのに期待値50枚
必要になると言う訳です。
累計してみると残5〜残2に必要な枚数が64枚、最後の1枚で50枚となるので
最後の1枚に辿り着いた時点でようやく折り返し。
まだ半分も残ってる事になります。
途中までは比較的スムーズなのに
最後の一枚が修羅場なわけだ。
さてここからが
どうやってこれら枚数を導き出したかの理論的な解説。
ま、実は昔のコラムですでに一度書いた事あるのですが(^^A;
「N枚コンプリートの確率」
実際の数字を出しながらやって見た方が直感的にわかりやすいでしょうので
ここでまた実演します。
とは言え当方モバゲーはやらないので
そもそも母集団(=カード枚数、および出現確率)がわからない。
そこでデータから逆算してみる事にします。
某有名モバゲーゲームAをサンプルに使います。
データ:
・ガチャ1回300円
・特定のカード5種類を揃えるとガチャコンプ
・カード総枚数不明(X)
・一般的な話ではコンプまでに2万半ば〜4万円が必要
・全てのカードは均一に出ると仮定する。
(↑実際はウェイト付けがあって均一ではないのでしょうが、
それでも正しい答えが出るのでこの仮定は行って構わない。一般性を落とさず問題を簡略化してるだけ。)
さてまずはX、カードの総枚数を推定する所からスタートします。
ここは本来システムを知っていれば出せる事なのですが、
メーカー側がガチャの確率を公表してないので(そもそも公正な抽選なのかも不明なのですが・・・)
こちら側から逆算で母集団を推定してやります。
スタート:
いま5枚ガチャコンプをしようとしています。
仮に1ガチャ行うと、総枚数Xの中から目的のカード5種類のどれでもいいから一枚を引く確率は5/X。
引けるまでに必要な期待値は確率をひっくり返すのでX/5枚。
この後にX/5枚引いて5種類の中から1枚をゲットしたとします。
残り4枚。
次にガチャを行うと、総枚数Xの中から目的のカード4種類のどれでもいいから一枚を引く確率は4/X。
引けるまでに必要な期待値は確率をひっくり返すのでX/4枚。
この後にX/4枚引いて4種類の中から1枚をゲットしたとします。
残り3枚。
次にガチャを行うと、総枚数Xの中から目的のカード3種類のどれでもいいから一枚を引く確率は3/X。
引けるまでに必要な期待値は確率をひっくり返すのでX/3枚。
この後にX/3枚引いて3種類の中から1枚をゲットしたとします。
残り2枚。
次にガチャを行うと、総枚数Xの中から目的のカード2種類のどれでもいいから一枚を引く確率は2/X。
引けるまでに必要な期待値は確率をひっくり返すのでX/2枚。
この後にX/2枚引いて2種類の中から1枚をゲットしたとします。
残り1枚。
次にガチャを行うと、総枚数Xの中から目的のカード1種類を引く確率は1/X。
引けるまでに必要な期待値は確率をひっくり返すのでX/1枚。
この後にX/1枚引いて最後の1枚をゲットしたとします。
さて、結局トータルでは
X/5+X/4+X/3+X/2+X/1 = 274X/120
枚のカードを引いたことになります。
ガチャが1回300円、コンプまでに2万半ば〜4万円が必要との事ですから
平均を取って32500円=108ガチャが必要と考えます。
よって
274X/120 = 108
X = 47.3枚。切りの良いところで四捨五入して50枚。
これでわかりました。
すなわち某有名モバゲーゲームAのシステムは:
・ガチャ1回300円
・カード総枚数50枚
・全てのカードは均一に出ると仮定する
・特定のカード5種類を揃えるとガチャコンプ
こんな感じ。
「全50枚、均一」条件は問題を分かりやすくするために簡略化してると思ってください。
重要なのは「目的のカードは2%で出る」と仮定する事で、それさえわかっていれば
実際の総枚数、および出現確率がどうであろうと
以下の計算は成り立ちますので。
システムがわかった所で、検算&わかりやすさの為にもう一回計算しましょう。
いま5枚ガチャコンプをしようとしています。
仮に1ガチャ行うと、総枚数50枚の中から目的のカード5種類のどれでもいいから一枚を引く確率は5/50。
引けるまでに必要な期待値は確率をひっくり返すので50/5枚。
この後に50/5枚引いて5種類の中から1枚をゲットしたとします。
残り4枚。
次にガチャを行うと、総枚数50の中から目的のカード4種類のどれでもいいから一枚を引く確率は4/50。
引けるまでに必要な期待値は確率をひっくり返すので50/4枚。
この後に50/4枚引いて4種類の中から1枚をゲットしたとします。
残り3枚。
次にガチャを行うと、総枚数50の中から目的のカード3種類のどれでもいいから一枚を引く確率は3/50。
引けるまでに必要な期待値は確率をひっくり返すので50/3枚。
この後に50/3枚引いて3種類の中から1枚をゲットしたとします。
残り2枚。
次にガチャを行うと、総枚数50の中から目的のカード2種類のどれでもいいから一枚を引く確率は2/50。
引けるまでに必要な期待値は確率をひっくり返すので50/2枚。
この後に50/2枚引いて2種類の中から1枚をゲットしたとします。
残り1枚。
次にガチャを行うと、総枚数50の中から目的のカード1種類を引く確率は1/50。
引けるまでに必要な期待値は確率をひっくり返すので50/1枚。
この後に50/1枚引いて最後の1枚をゲットしたとします。
さて、結局トータルでは
50/5+50/4+50/3+50/2+50/1 = (274×50)/120 = 114.2
枚のカードを引いたことになります。
これはコンプまでに必要な枚数の平均です。
別の言い方をすると
Aさんはコンプまでに100枚引いた、Bさんはコンプまでに170枚引いた、Cさんは50枚、Dさんは300枚、・・・・
などの事例があったとして、これら全ユーザーの平均を取ると114.2枚に集束してゆくわけです。
1ガチャ300円ですから114.2回ガチャを行えば
300×114.2=34250円
確かに実測数値と一致することが確かめられました。
長くなったので次回に続きます。
「CG(2012/05/09)」
今日のCG。マンガ仕立て。

セリフがバグってるのは文字化けではなくわざとです。(汗)
「言葉はわからないけど、なんとなく言いたい事はわかる」って感じを目指してみました。
ちなみに私はCG製作にはIllustStudio(公式HP)ってソフト使ってます。
ペンタブレットのIntuos4買ったときにバンドルされてて、
「始めて聞く名前のソフト。
ま、無料で貰ったし。とりあえず一度は触って見るか」
程度の気持ちで使い始めたのですが
これが予想以上の高機能・高性能でそのまま居座っちゃいました。
マンガ作成の為のツール類(集中線・平行線・同心円定規など)も用意されてて
漫画チックな表現描き込みに便利便利。
国産ソフトだけあって
日本人的なイラスト作成の需要に最適化されてるのが◎。
「テンキー(2012/05/05)」
あとオレンジのテンキーの方も直しておきました。

・故障箇所:Enterキー
・症状:押した時の感触が悪い
・原因:メンブレンのゴム部分がへたっていた。
・行った対策:左上のTABキーを引っこ抜いて、ゴムをEnterキーに持ってきた。
・副作用:おかげでTABキーは使えなくなりましたが。^^A;
どうせそちらは元から使ってなかったキーなので問題なし。
これはこれで全力で修理して延命させておきましょう。
「テンキー(2012/05/03)」
お気に入りのテンキーが壊れかけな件につきまして。

代替えとして取り急ぎで安物を買ってきたのですけど

これが失敗だった。キータッチが全然好きじゃない。許容範囲外。(汗)
やっぱりしっかりした物買おうと
大手家電量販店へ行って
パソコンコーナーを物色してきました。
この店舗には売り場にある全てのキーボード・マウスに
試し打ちモデルが置いてあって
買う前に感触がわかるので超便利。
30分ほどかけながら
端からは端までタイピングし続けて品定め。
・・・
・・
・
あ、あれ。
しっくり来ない。
個人的にはどれも「フニャっ」としたしまりのない打ち心地で、

このBuffalo BASTK01級の「サクッ」な快適モデルに出会えなかった。
Buffalo,iBuffaloの現行製品ラインナップにすらない。
これ、なにげに名器だったんだ・・・
とは言え在庫の奥の奥まで探したらなんとか見つけました。
Buffalo BTKU2H03PWHA

BASTK01と同時期に作られた姉妹品ですね(違いはUSBハブ機能の有無)。
店頭で触ったら打ち心地はBASTK01と全く同じ。これだ!
よくも見つかったくれました(^^A;
Buffalo自体がすでにiBuffaloに社名変更してますから、
この(旧)Buffaloモデルは完全に廃盤。店頭在庫にかろうじて残ってるのが最後のはず。
大切に使ってゆこう。
トップへ
2012年04月の日記
2012年の日記
最新の日記


















