ポアンカレ予想 世界一周してロープを回収できる図形は、球のみか? 8/15
あああ、ややこしくなってきた。(汗)
マゼランの時代には
「世界を一周できれば球体」
ぐらいに思っていたのですが
ところがよくよく考えてみれば
「世界を一周できる形」
には
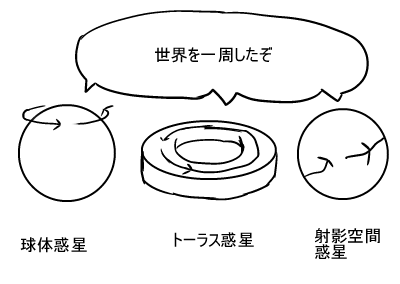
球体/トーラス/射影空間の三種類の異なる構造
(球体=一周でロープを回収できる。
トーラス=一周、二周でロープを回収できない。
射影空間=一周でロープを回収できない、二周で回収できる)
を持つ図形が見つかってしまったのです。
もちろん、
この三者を比較すると
「一周でロープを回収できる」
性質を持っているのは
球体だけなのでそこで区別はつくのですが。
・・・
・・
・
だがしかし、
さらによくよく考えてみれば、
もしかしたら球体/トーラス/射影空間に続く
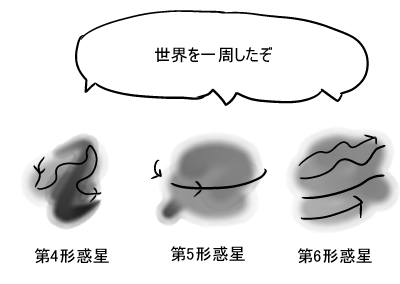
第4、第5、第6・・・の新しい惑星の形があるかもしれないし、
それら未知の図形の中には
「世界一周でロープを回収でき、かつ球と同型」ではない
構造が存在する可能性があるのでは・・・?
少なくとも「ない」とは言い切れません。
そこで!
ポアンカレ予想なのです。
すなわち
「世界一周してロープが回収できる図形は 球のみである」
との仮説に確かな根拠、
数学的証明を与える必要があるとポアンカレは考えました。
西暦1904年の出来事。
うーん。驚くべき事に。(^^A;
「世界一周してロープが回収できる図形は 球のみである」
と言う言明は
よくよく考えてみると。
実に全く、自明な事ではないのです。はい。
前ページ 次ページ
トップへ

