ポアンカレ予想 世界一周してロープを回収できる図形は、球のみか? 1/15
今年の数学コラムはポアンカレ予想です。
まずは数学的な定義から。
ポアンカレ予想とは
「単連結な三次元閉多様体は、三次元球面と位相同型である(と予想する)」
と言う言明の事です。
平たく言うと
「どこにロープを置いても回収できる風船は球に変形できるし」
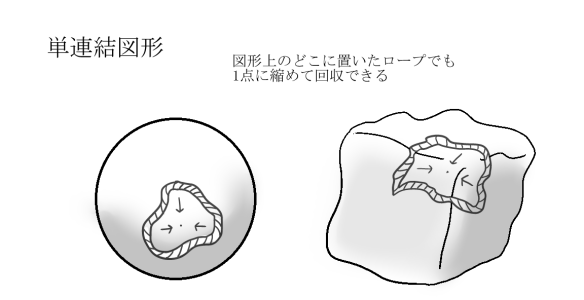
(単連結な三次元閉多様体は、三次元球面と位相同型である)
「ロープが回収できないルートのある風船は球に変形できない」
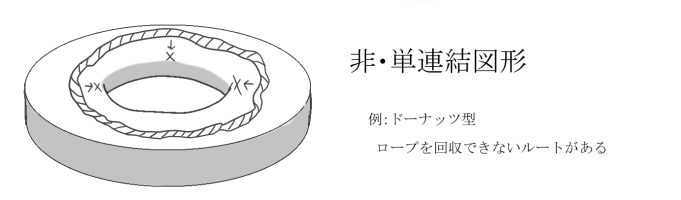
(単連結でない三次元閉多様体は、三次元球面と位相同型ではない)
と言っています。
こうやって図に描くと
なんか凄く簡単そう・・・
と言うか自明に見えるんですけどねー。(´д`;
ところが実際そうではない。
それは我々が「図形」と聞くと
普段見慣れたリアルな物体しか頭に
思い浮かばないから
そう思ってしまうだけで。
数学的な「図形(多様体)」と言うと
例えば射影空間
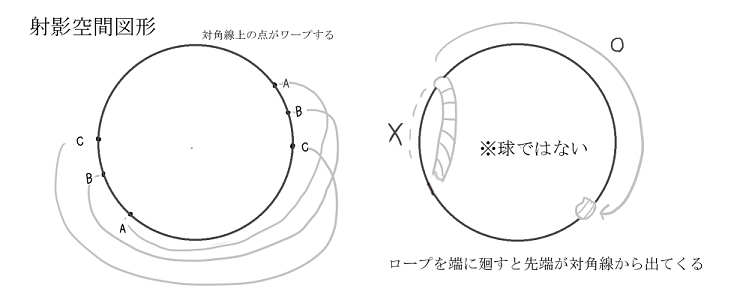
も二次元図形です。
この図形レベルになるとそもそも
「ロープを置いて回収できるのか?(ロープの置き方によっては回収できないルートがあるか?)」
がよくわかりませんし、^^;
さらにもし回収できるとしたら、このヘンテコな図形を球に変形させる手法の明示。
もしくは変形できないなら出来ない事への証明をしなければいけません。
後者なら「単連結であるが、球と位相同型ではない」。ポアンカレ予想の否定になります。
射影空間よりももっと複雑な図形もあります。
その場合にはどうか?
---------------
意外に思われるかもしれませんが
「図形はロープが回収できるか?」と言う性質と
「図形は球に変形できるか?」と言う性質は
別物です。
だってそもそも!
前者は「図形Aについての性質」を述べてる1項関数。f(A)形式。
後者は「図形Aは図形Bと同じ形か」を述べてる2項関数。g(A,B)形式。
文法のレベルからして違うぐらい別の事を喋ってるんですから
両者が一致する必然性はどこにもないんです。(驚愕)
・・・だからこの問題はパッと見で思うよりも
全然、全く、自明な話ではないんですよ。(汗汗汗)
ポアンカレ予想が100年も未解決だったのは
「もしかしたら。ロープは回収できるが、球に変形できない図形があるかも知れない」
可能性を数学者が捨てきれなかったから。
次ページ
トップへ


