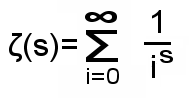 (式1)
(式1)| 1 + 2 + 3 + 4 + 5 + 6 + ・・・・ = -1/12 |
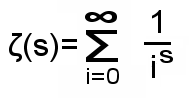 (式1)
(式1)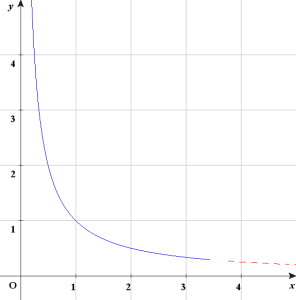
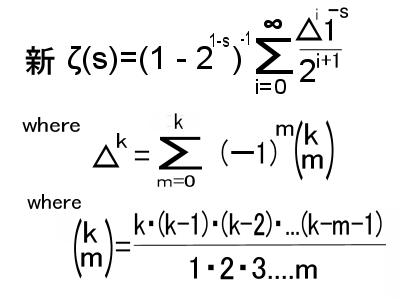 (式2)
(式2)| 1 + 2 + 3 + 4 + 5 + 6 + ・・・・ = -1/12 |
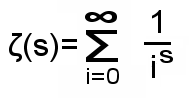 (式1)
(式1)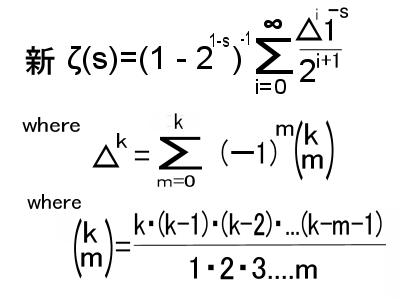 (式2)
(式2)| 1 + 2 + 3 +・・・・ = 旧ζ(1) →拡張→ 新ζ(1)= -1/12 すなわち 1 + 2 + 3 +・・・・ = -1/12(?) |
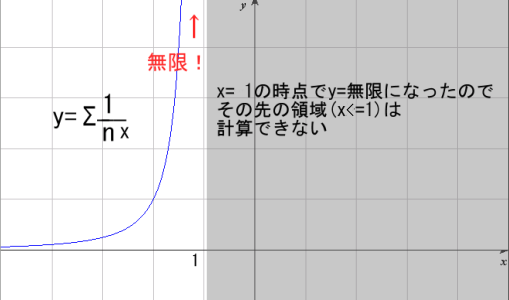
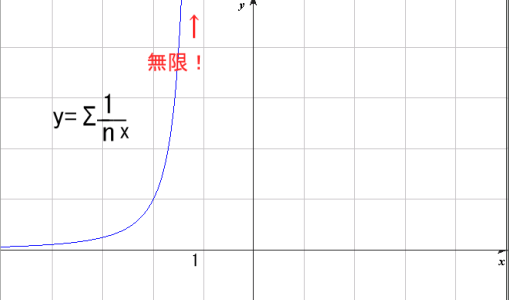
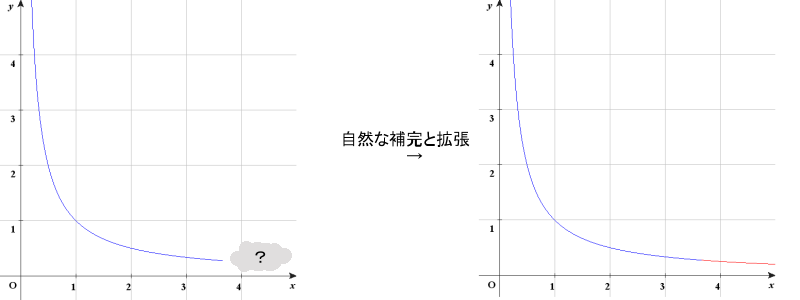
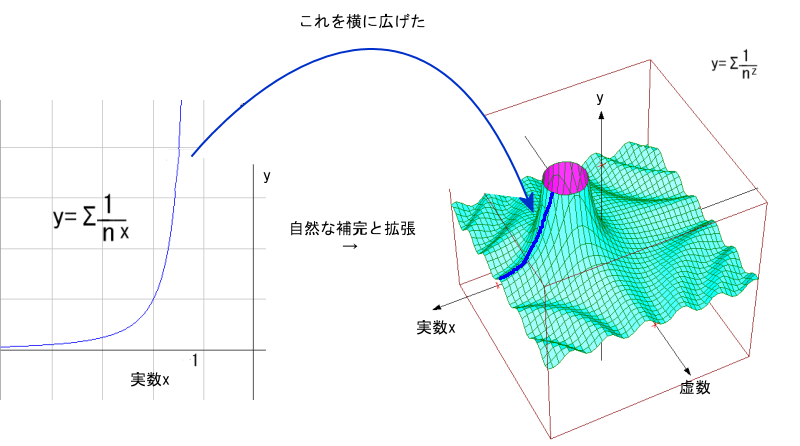
なお、本来のゼータ関数のグラフは
こんな感じなのですが
一般にはグラフは左から右へとあがってゆくノの字型の方が見慣れていると思いますので
このページでは変則的にX軸の左にいくほどプラス、右に行くほどマイナスとして描きます。
見た目が左右反転しているだけで他に問題はないので気にしないでください。
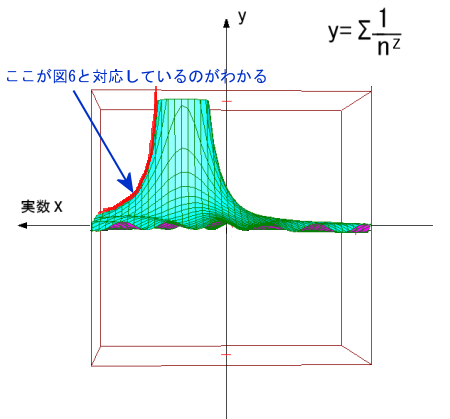
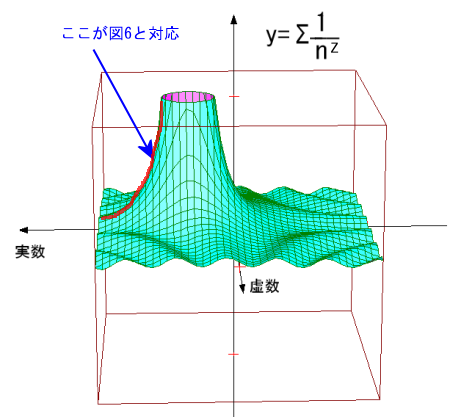
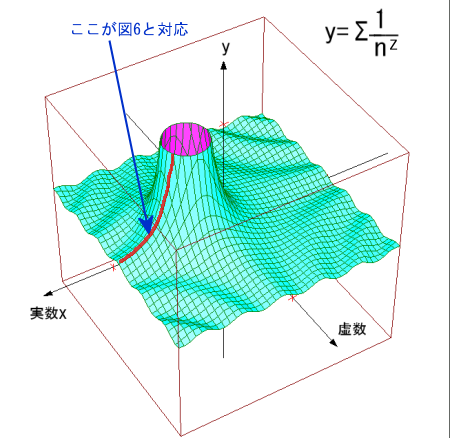
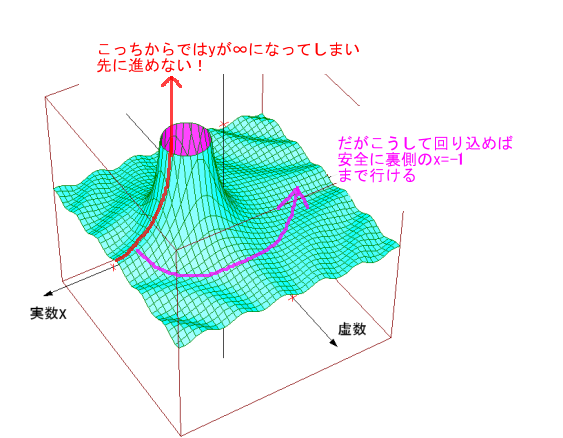
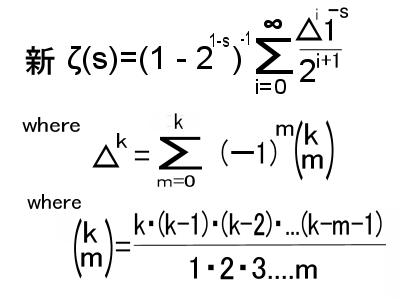
| 旧ζ(-1)=1 + 2 + 3 +・・・=計算不能。 新ζ(-1)=((1-2(1-(-1))(-1))・Σ(△i/2(i+1)) =-1/12 |
| 1 + 2 + 3 +・・・・ =(不可能だがもし答えがあるとするなら)-1/12 |
| 1 + 2 + 3 +・・・・ =-1/12 (解析接続による評価) |
| (1 + 2 + 3 +・・・・ )のキャラクターは-1/12 |
| 1 + 2 + 3 +・・・・ =-1/12 (答えがあるとするなら) |