「N枚コンプリートの確率(2009/10/15)」
よく話題に出るので「全n種類の○○コンプリート確率」をここにまとめておきます。
この問題は例えば「全100種類あるトレカを何枚買うと全種類コンプリートできるか」の平均枚数を求める問題です。
さっそく計算してみましょう。
まず、一枚目を買うときは100%新規カードが出るので最初の一枚は1回で手に入ります。
次の一枚を買うと1/nですでに手持ちのカードと重複、(n-1)/nで手持ちにない新規カード。
よって次の新規カードが出るまでには確率をひっくりかえして期待値としてn/(n-1)枚のカードを買う必要があります。
次の一枚を買うと2/nですでに手持ちのカードと重複、(n-2)/nで手持ちにない新規カード。
よって次の新規カードが出るまでには確率をひっくりかえして期待値としてn/(n-2)枚のカードを買う必要があります。
次の一枚・・・
で計算していくと
全種類コンプリート、すなわちこれがn種類まで増えるまでには
期待値総枚数=n/n + n/(n-1) + n/(n-2) + n/(n-3) + ・・・ + n。
=n(1/(n) + 1/(n-1) + 1/(n-2) + 1/(n-3) + ・・・・ + 1/1)
の枚数が必要です。
(1/(n) + 1/(n-1) + 1/(n-2) + 1/(n-3) + ・・・・ + 1/1)
の部分にはあいにく簡単な式がありませんのがこれはlog(n)で近似できます。
どういう事かと言うと(1/(n) + 1/(n-1) + 1/(n-2) + 1/(n-3) + ・・・・ + 1/1)
=(1/1 + 1/2 + 1/3 + ・・・・ + 1/(n-2) + 1/(n-1) + 1/(n))
=下図の赤い面積
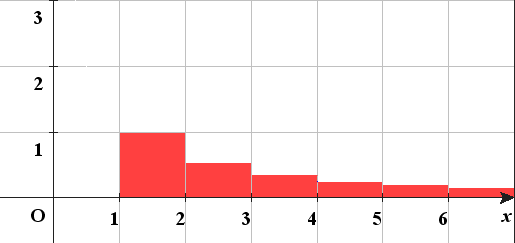
これをy=1/xグラフ
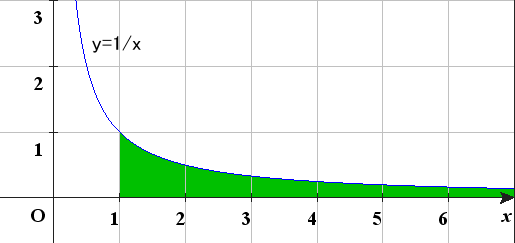
の緑の面積で近似しようと言うのです。
緑の面積は積分して∫n1(1/x) = log(x)|n1=log(n)-log1 = log(n)-0 = log(n)
と言うわけです。
もちろん近似なので実際は誤差が出ますし緑面積<赤面積なので
本当はもっと多く必要ですが
目安としてのおおまかな値は算出できます。
計算式に戻りますが
期待値総枚数=n(1/(n) + 1/(n-1) + 1/(n-2) + 1/(n-3) + ・・・・ + 1/1)
=約n(log(n))
よって「全n種類の○○をコンプリートするまでに必要な期待値枚数は約n×log(n)」。
詳細は省きますが赤面積が1/x緑面積で完全に覆い被さるよう多めに見積もるならn×log(n) + nと思えばいいでしょう。
例えば全100枚のトレカがあってそれを普通に買いながらコンプリートしたいならおおよそ
100×log(100)≒100×.4.61=461枚必要と言うわけです。
(ここのlogと書かれてる物は一部の関数電卓では「ln (自然対数ログ)」と書かれているボタンが正解でして
「log(10対数ログ)」ボタンの方ではありません。
100のログを求めて4.605170186が出てくる方です。
なお数学では常にログ=自然対数ログなのでログを取ると言われれば必ずlnボタンです・・・)
最新の日記へ

