- 1.幅a、高さbを持つ長方形の面積はaxbである。
-
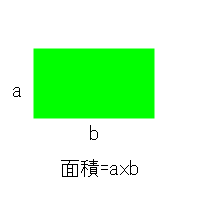
基本長方形の面積は常識的であるべきと言っています。 - 2.面積は図形の平行に不変である。m(A) = m(A+x)
-
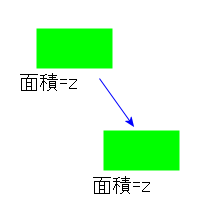
図形を動かしてもその面積は変化しないと言っています。当たり前です。 - 3.面積は加法性を満たす。m(A+B)=m(A)+m(B)。
-
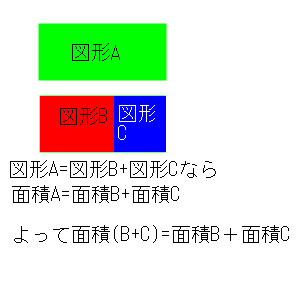
図形をどう分割した所で合計の面積は変化しないと言っています。当たり前です。
そして以上「1)〜3)の性質全てを満たす面積関数mによってm(A)=aで計算された非負実数値aをAの面積」と呼ぶ。
- 1.幅a、高さbを持つ長方形の面積はaxbである。
基本長方形の面積は常識的であるべきと言っています。
- 2.面積は図形の平行に不変である。m(A) = m(A+x)
図形を動かしてもその面積は変化しないと言っています。当たり前です。
- 3.面積は加法性を満たす。m(A+B)=m(A)+m(B)。
図形をどう分割した所で合計の面積は変化しないと言っています。当たり前です。
です。
- 4(希望).面積関数mは全ての図形に対して面積を算出する。
どんな図形でも面積を測る事ができる。