 面積の測れないとてつもない図形
面積の測れないとてつもない図形
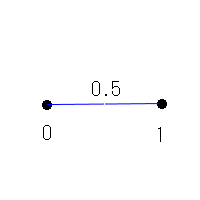
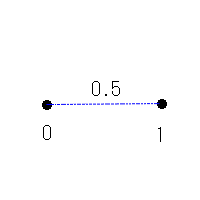
集合Aに対するルベーグ外測度(長さ)とは
m*(A)=inf{Σ|Ij|:Ijは開区間でA⊂∪Ijなるもの}。
を持って定義される。
ちなみに前節の「開区間群の長さの合計を、集合Aの長さとする」の部分、
「長さを定義するのに、長さを使ってるじゃん?それっておかしいじゃん?」と思われるかも知れませんが
開区間(a,b)の長さはb-aとして定義で確定しますので問題ありません。
開区間とは言ってみれば物差しです。
ルベーグ外測度は「物差しじゃ普通測れないような不可解な図形の長さ」を物差しで測れるようにするための測量の方法論を提示しようと言っているのであって、
物差し自体の長さは測量せずとも確定しています。それぐらいはないと本当にどうしようもないですから。(汗)
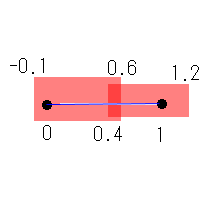
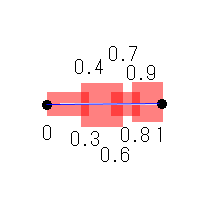
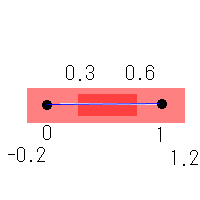
 面積の測れないとてつもない図形
面積の測れないとてつもない図形