内角の和が270°の正三角形
「数学コラム 内角の和が270°の正三角形 (2015/05/20)」
唐突に数学コラム。
命題:
「内角の和が270°の正三角形を作れ」
と言う問題を考えます。
さて・・・
「三角形の内角の和は180°」
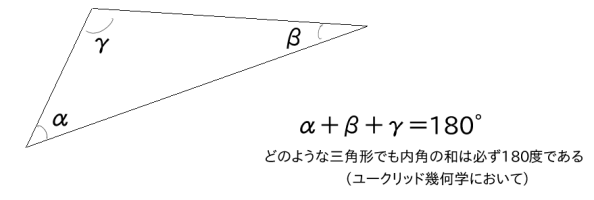
これは小学校時代に誰しも習うことであり、
常識だと思うのですが。
・・・実は違うんですね! これが^^;
数学的に言って内角の和が>180°、もしくは<180°になる三角形はあります。
非ユークリッド幾何学や
マニフォルド(多様体)と呼ばれる分野では普通に出てきて
内角の和が270°にもなれる。
答えは・・・空間を曲げます。
もっとシンプルに説明すると球体を持ち出して、
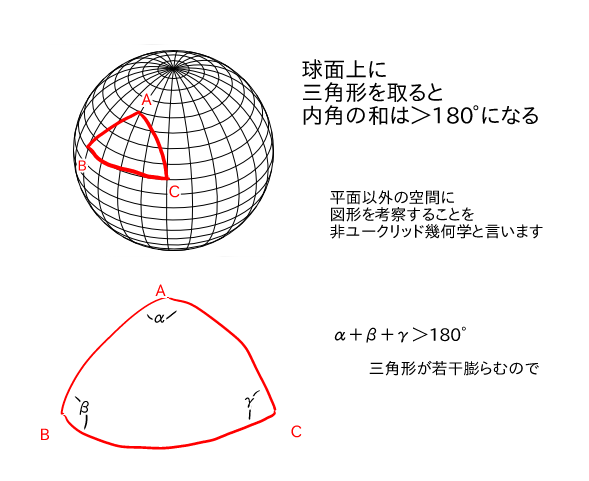
このような三角形を球面上に描けば内角180°以上の三角形が作成できます。
あー、種を明かされてみれば驚くほど簡単だね。
さらに特殊なケースとしてAを北極、BCを上半球4分割の地点に持ってくれば(緯度はどこでもいい)
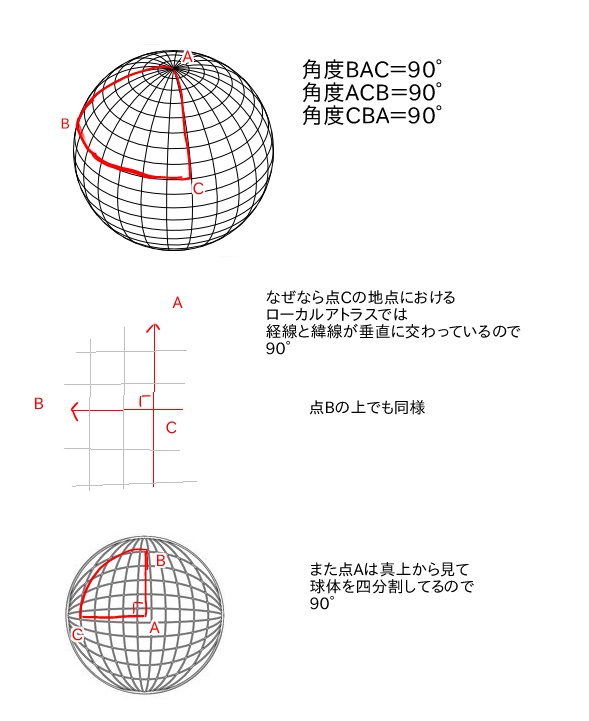
ABCの内角の和は270度になります。
理由は:
(1)角ABCは経線と緯線が垂直に交わる地点なので角度は90度。
(2)角CBAは経線と緯線が垂直に交わる地点なので角度は90度。
(3)角BACは頭上から見ると球体を4分割するので角度は90度。
よって三角ABCの内角の和は270°になります。
さて・・・
ここで問題は「いやちょっと待て。ABCは三角形と言えるか?」ですよね。
なにしろ辺がゴムのように膨らんでる。
辺が直線で構成されてなければ三角形ではないとの疑問がつく。
ところが・・・やっぱりABCは三角形なんですねー。
なぜなら
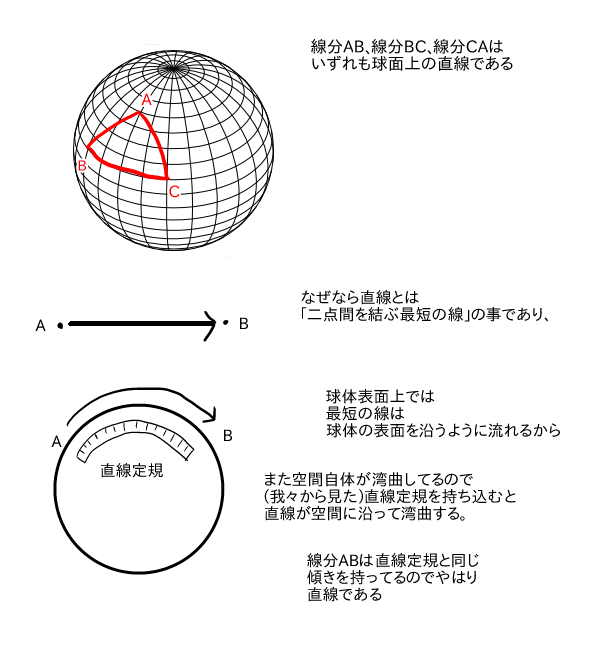
直線とは「二点間を結ぶ最短の経路」の事であり
線分ABは球面上で点Aと点Bを結ぶ最短の経路。
直線の条件を完璧に満たしているので。
大切なのはこの場合
湾曲しているのは空間であり、
直線の定規も球体表面上では変形してしまう事実です。
球面上に住んでる人達には球面上しか利用するスペースはなく、
球体の厚みベクトルを知覚できません。
ドメインを球体表面に絞る限りは
線分ABが間違いなくAB間の最短であり、
また住民に取っても直線に見えている、
球体表面上の直線となります。
以上:
1.図形ABCには3つの点がある。
2.線分AB、線分BC、線分CAは全て直線である。
3.角度ABC、角度BCA、角度CABは全て90度である。
の理由によって
図形ABCは間違いなく
直線の辺を3つ持つ三角形であり、
かつ内角の和が270度となります。
さらに最初の命題に戻りますが「内角の和が270度の正三角形」
についてはもうちょっと条件を追加して
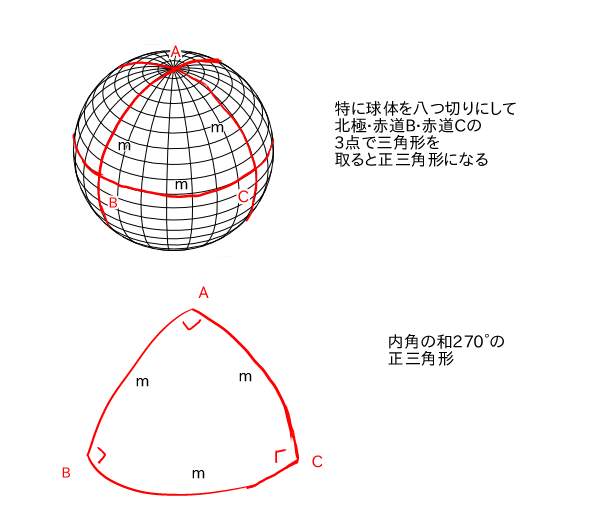
単純に球体を8つ切りして、その中の適当な一つを取れば達成できます。
いかがでしたでしょうか。
「三角形の内角の和は180°」って小学生の頃にも教えられるので
固定観念として覚えちゃって
普通は何の疑問も抱かないと思いますが^^;
非ユークリッド幾何学になると
「三角形の内角の和は180度とは限らない」「平行線と平行線が交わる(空間が閉じてる時)」「平行じゃない線が永遠に交わらない(空間が開いてる時)」
などの現象が普通に発生するんですね。
-----------------------
余談ですがここらの考え方。
点・線などの個別オブジェクト同士の関係性から、
それらを内包する空間が持つ性質へと考察の対象が移行したのは
現代数学の特徴でもあります。
例えばですね。
旧来では「直線=定規でひいた真っ直ぐな線」として考えられてきましたが
これでは球面上の物体には使えない。
それを「直線=最短の線」に定義しなおせば
平面・球面・その他空間のどこでも使えるようになって
こちらの方がオールマイティーに強い。
すなわち後者の定義の方が直線の本質は何たるかを
よりディープに捉えて、もっと進んだ理解になってるわけですね。
-----------------------
そこから出てきた座標と距離の抽象化。
強力な抽象化によって例えば
1つの関数式を空間上の1つの点として扱い、近い関数は隣接する点、全てのグループ関数が
空間全体を作るみたいな関数空間の考え方・研究ができた。
関数空間を使えば関数の性質を空間的に、個別の関数の外にあるメタ的高い視点から
limit・近似・変化・変形みたいな連続的に見る解析学の手法を導入できるようになって
超リッチになった。
特に微分・積分が使えるのは凄い。
微分積分は数学の一つの超ジャンルですからね。膨大な研究がされてて定理の山。そこに合流して理論を引っ張ってこれるようになった。
さらに関数空間を研究して得た成果は空間としての性質なので、
抽象化によって他のジャンルからも様々な概念を
点・空間へとコンバートすれば
空間に関する理論や定理を適用でき一気に研究が進む。
そんな事もありあちこちの数学者がこぞって空間に飛びこんで、なんでもかんでも点・空間にする。
上からも(他のジャンルからのコンバート)、下からも(空間を研究するためのツールとしての解析学)
空間に繋がり始めて活気づいた。
空間は重要。空間の研究こそがもっともホットなトレンド。
ここで成果を上げれば色々な問題が一気に解決する。
みんな空間に来て研究しろよーって流れになったんですね。100年ぐらい前です。
-----------------------
そこからさらに時代が進み、次第に空間の研究も煮詰まって限界が来ました。
そしたら今度は空間をタイプ別にわける
マップを作成して空間全体を上から見ようって計画が持ち上がって^^;
空間を生み出すジェネレーターとして環(ring)に着目した研究が始まり
スキーム論〜うんたら(長くなりすぎるのがカット)がちょい前。
ここ50年の数学の最新です。
トップへ




