「17角形とガロア理論 第15〜18章 (2025/8/18)」
はーい、ここがいっちゃん難しい所。
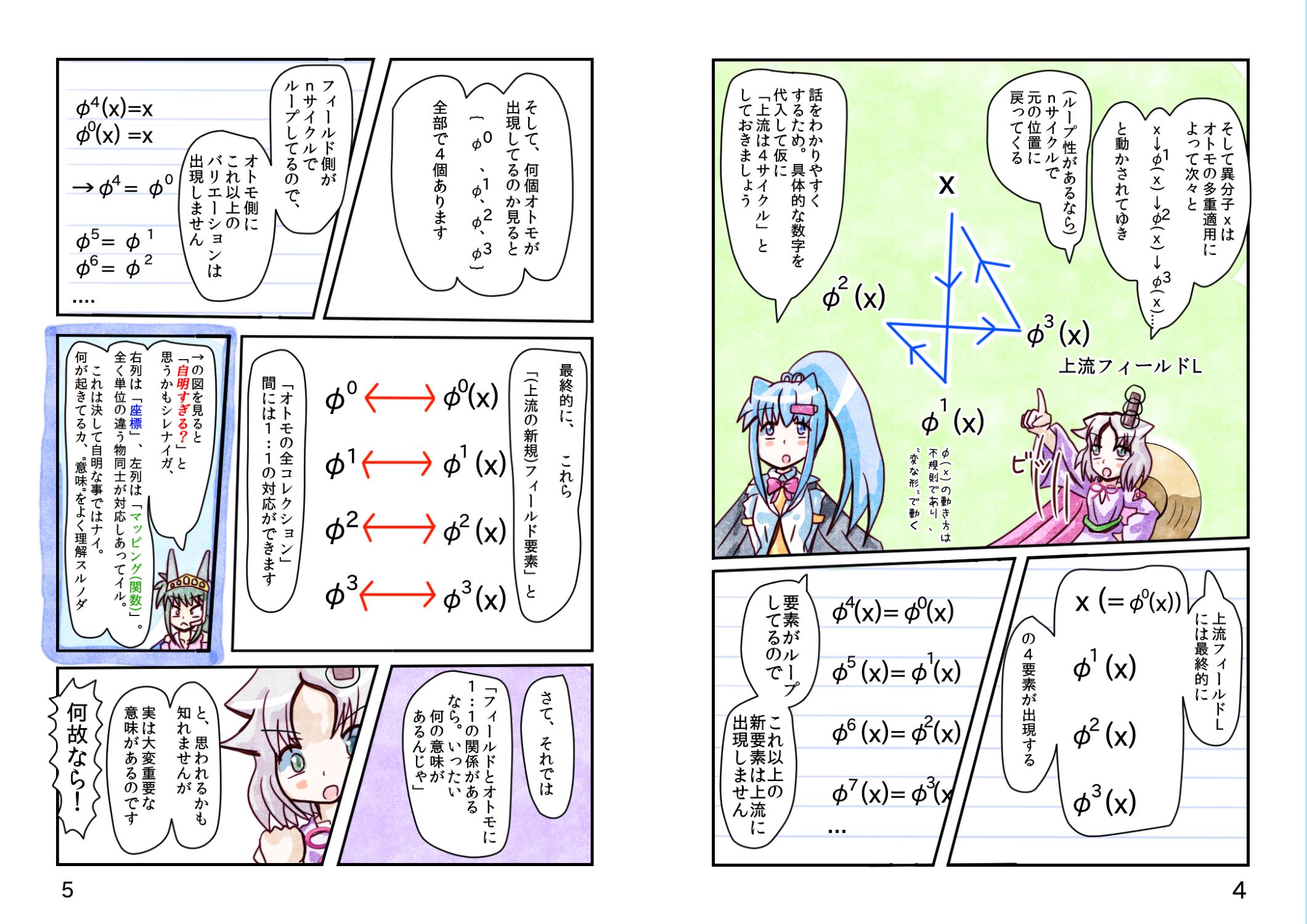
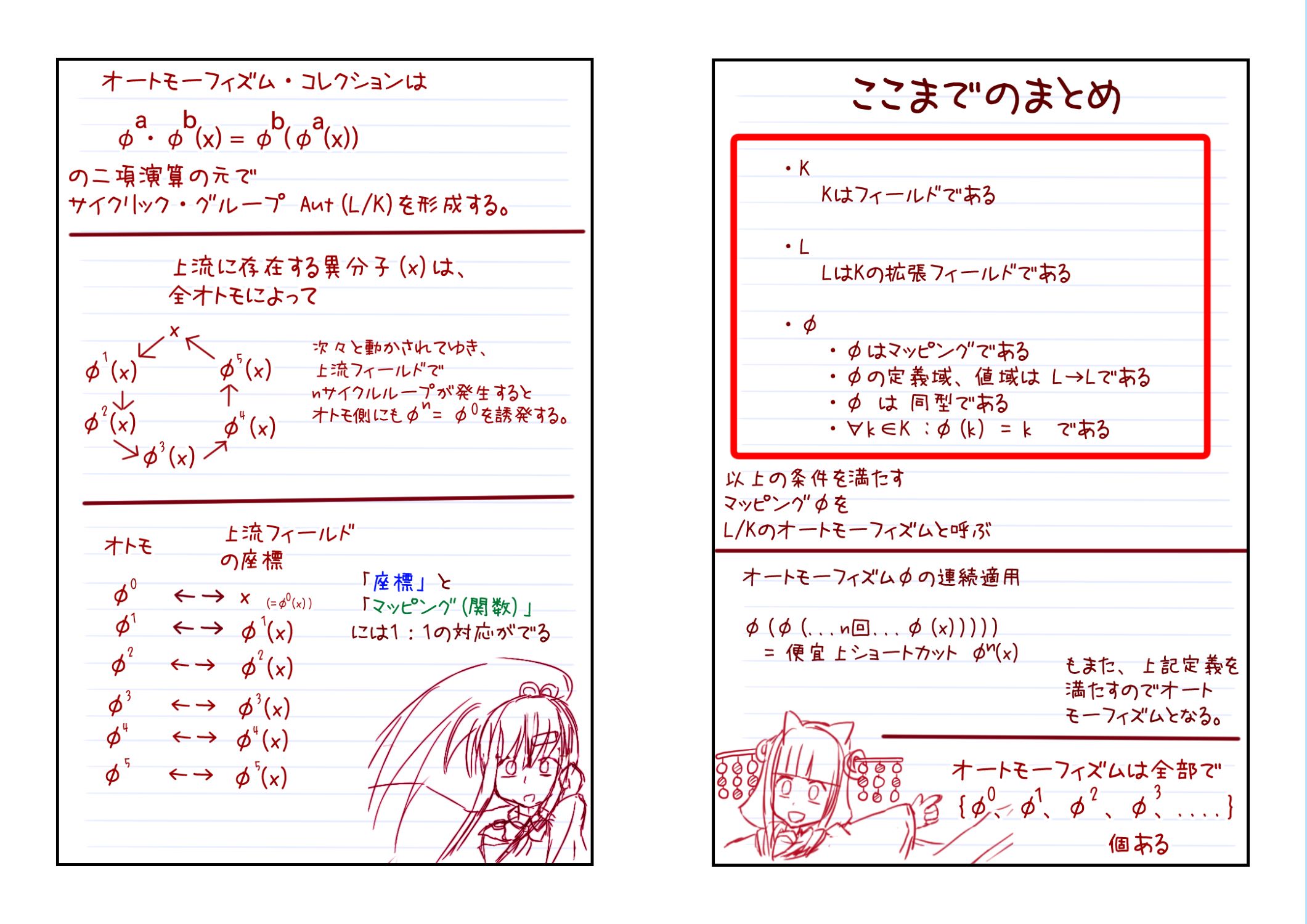
我々は今
基本フィールドKの、
拡張フィールドLの、
L→Lマッピングの、
Kを固定するオートモーフィズムφの、
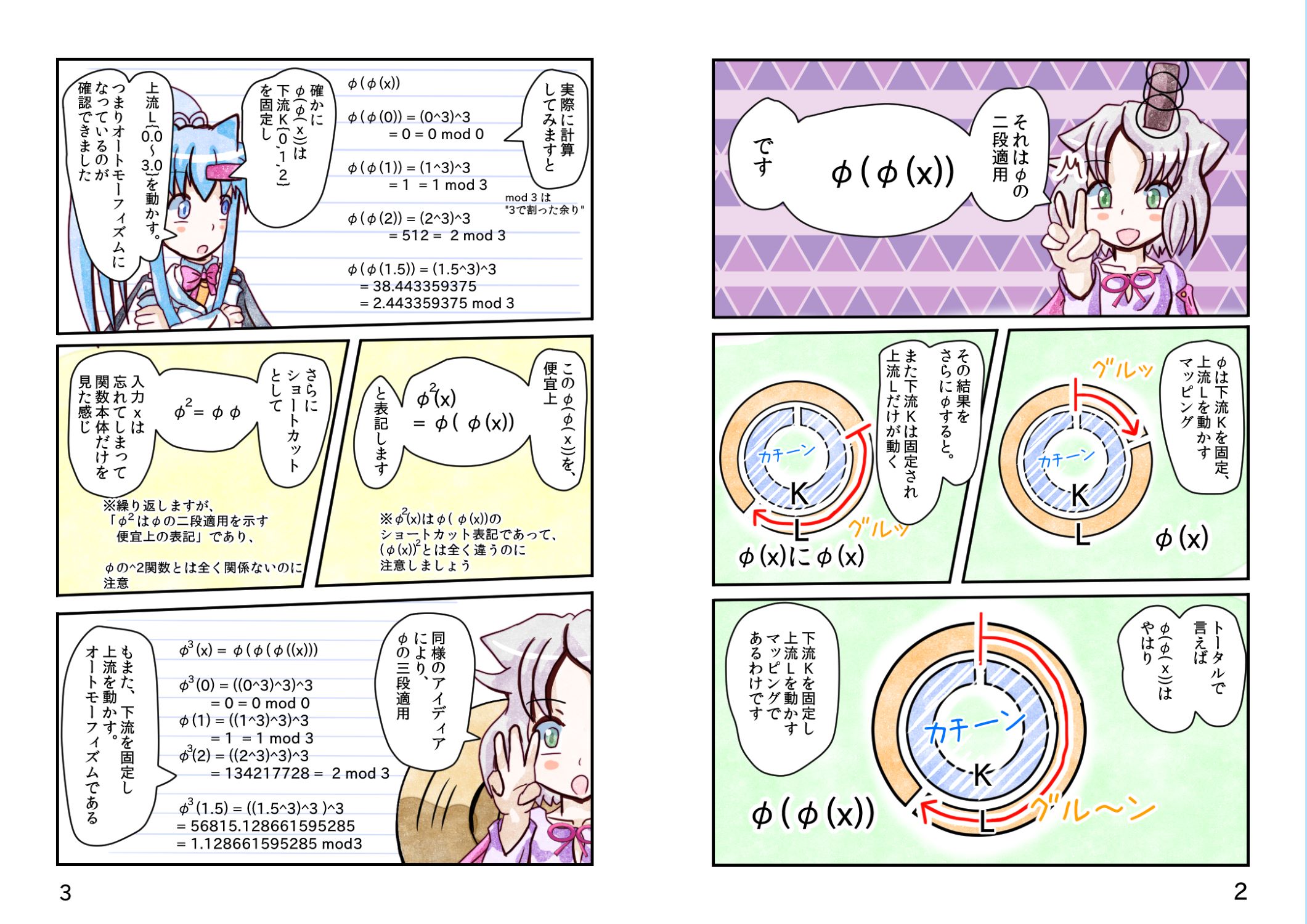
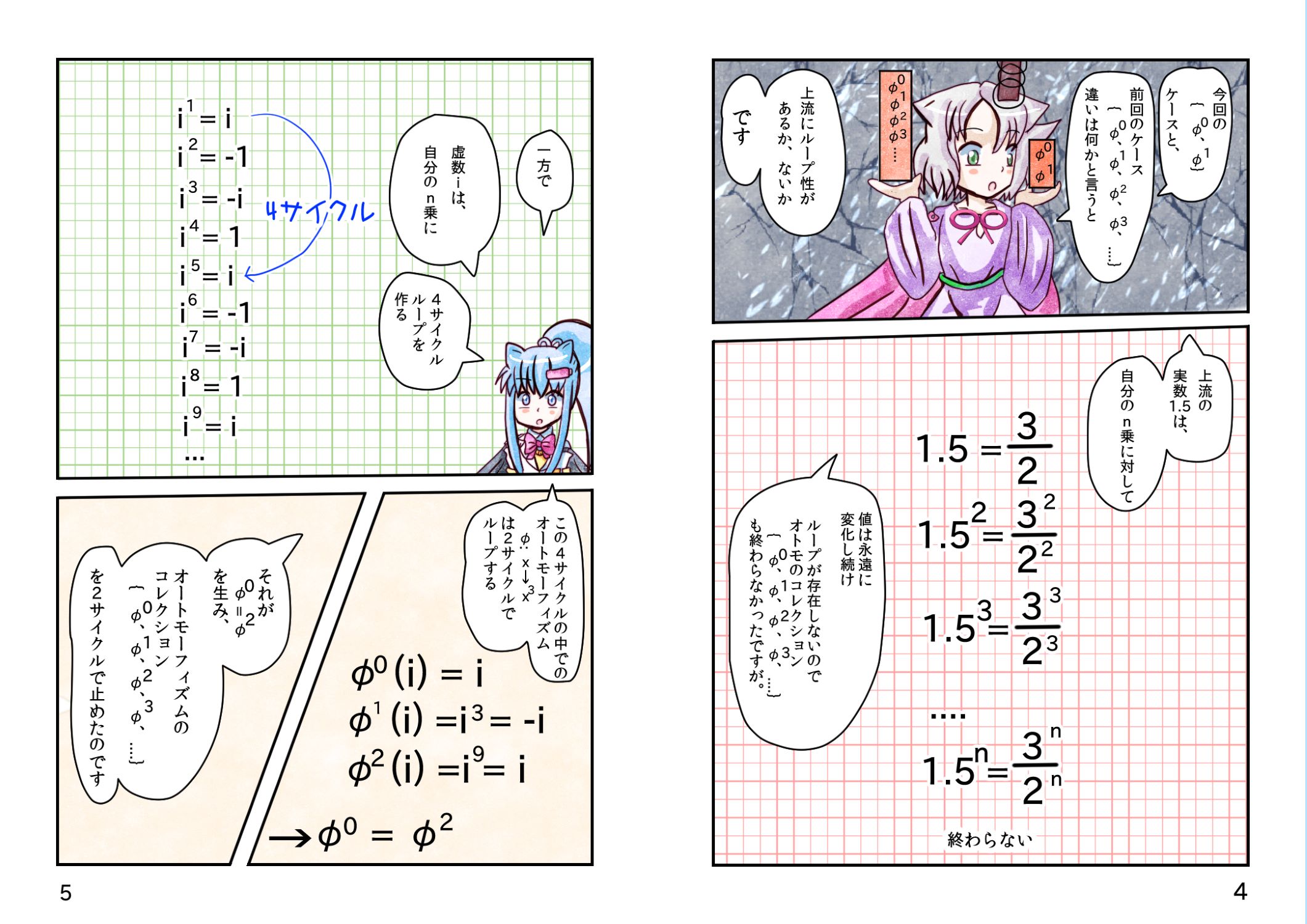
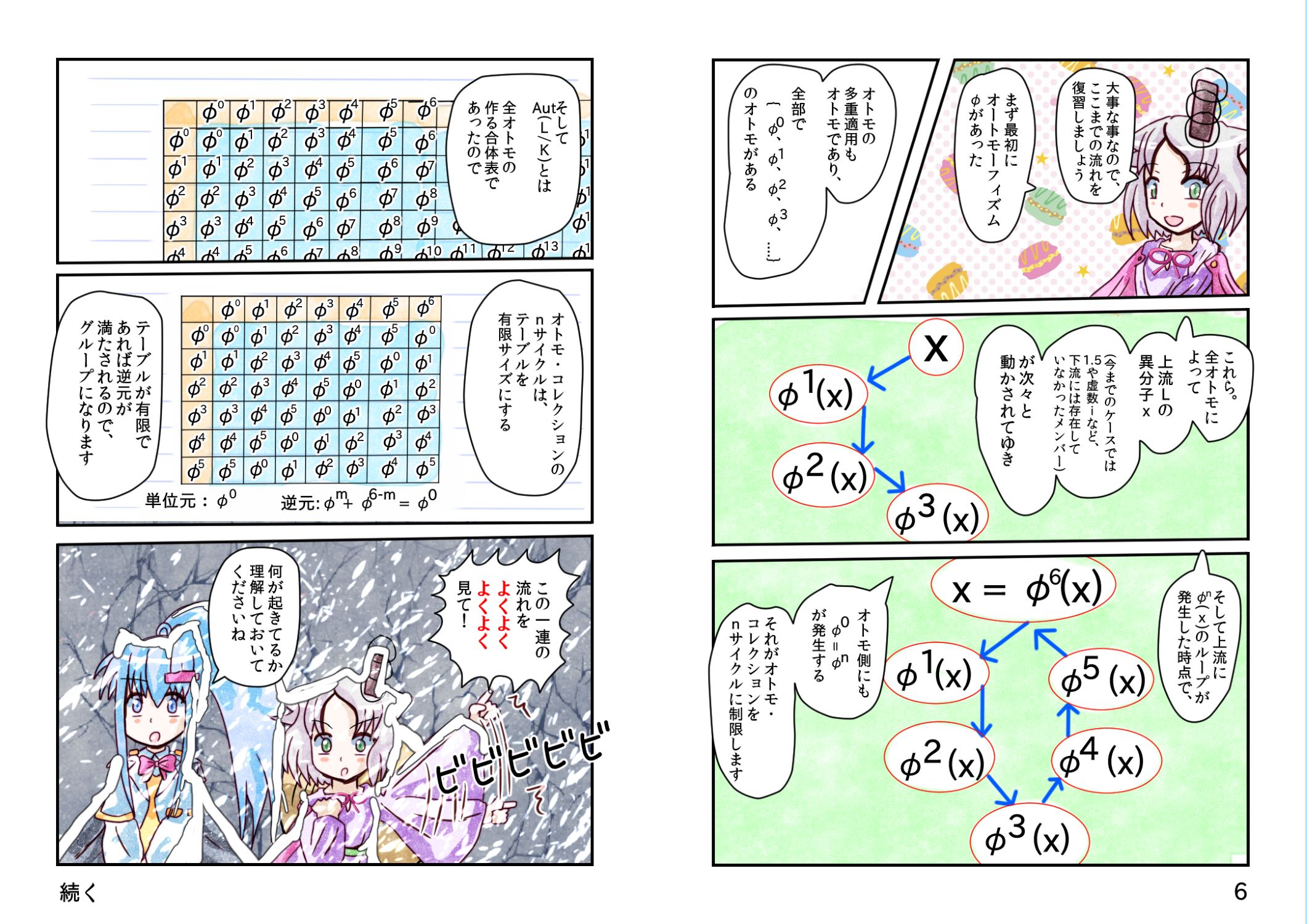
φ 多重適用の、
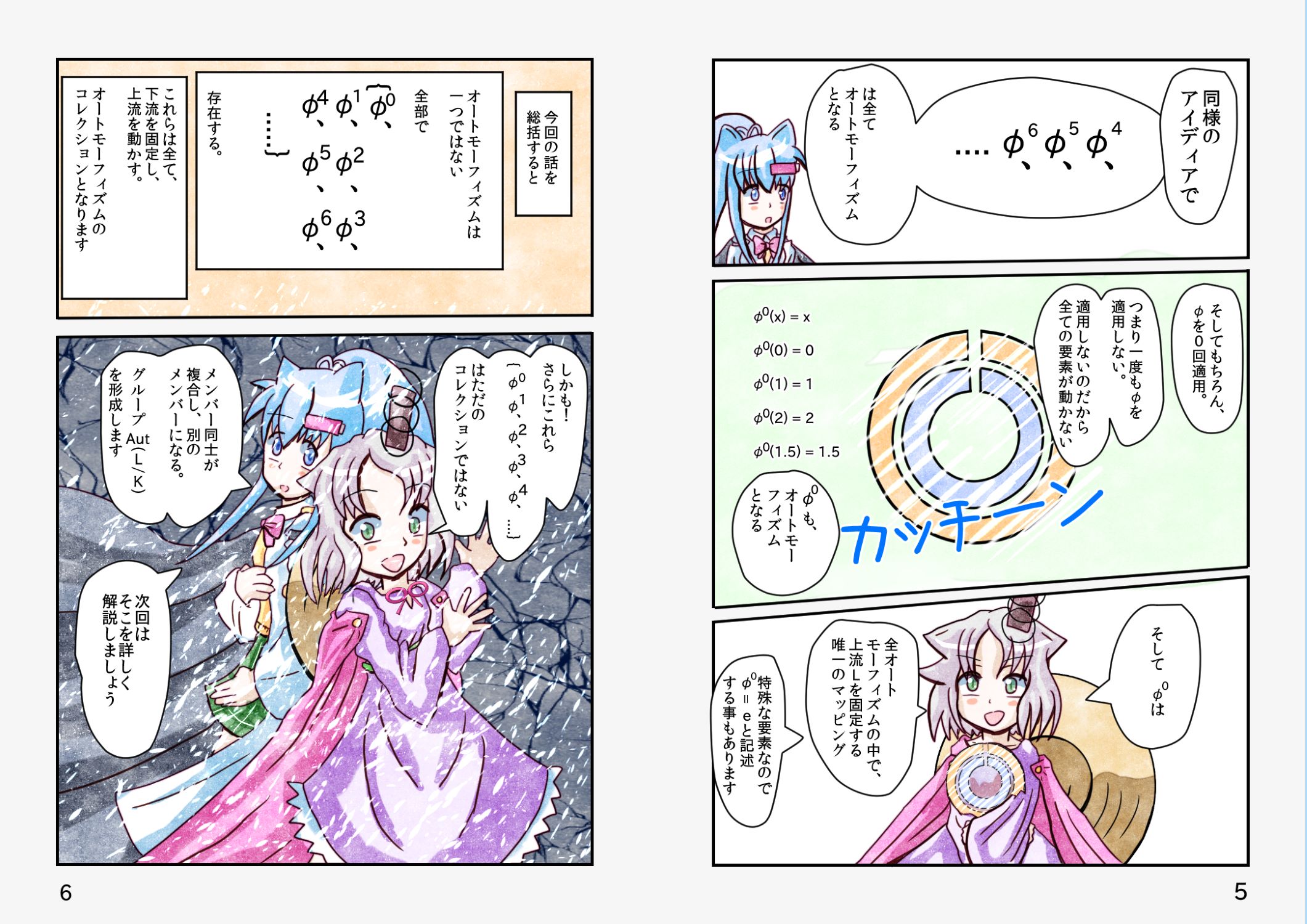
全 φ コレクションの、
二項演算 φ・φの、
グループ表Aut(L/K)
拡張フィールドLの、
L→Lマッピングの、
Kを固定するオートモーフィズムφの、
φ 多重適用の、
全 φ コレクションの、
二項演算 φ・φの、
グループ表Aut(L/K)
を考えています。
歴史的に言えば、この手法
オートモーフィズム
と言うのは
5次方程式
x5 + ax4 + cx3 + dx2 + ex1 + f = 0 (※)
の解法を考える途中に編み出されました。
300年間、誰も(※)の公式を発見できず。
「なんで公式が見つからないのか!」
その理由を、数学者のガロアが
フィールドの → オートモーフィズムの → グループ
による完璧な証明を見つけてた。
これをガロア理論と呼びます。
n角系の作図と言うのも、実は
x17 - 1 = 0
で記述する事ができ。
両者は本質的には同じであります。
(こちらは解けるパターンですが)
だから我々は今、ガロア理論を学んでるわけですね。
はい。
17角形とガロア理論 第15章 多重オートモーフィズム


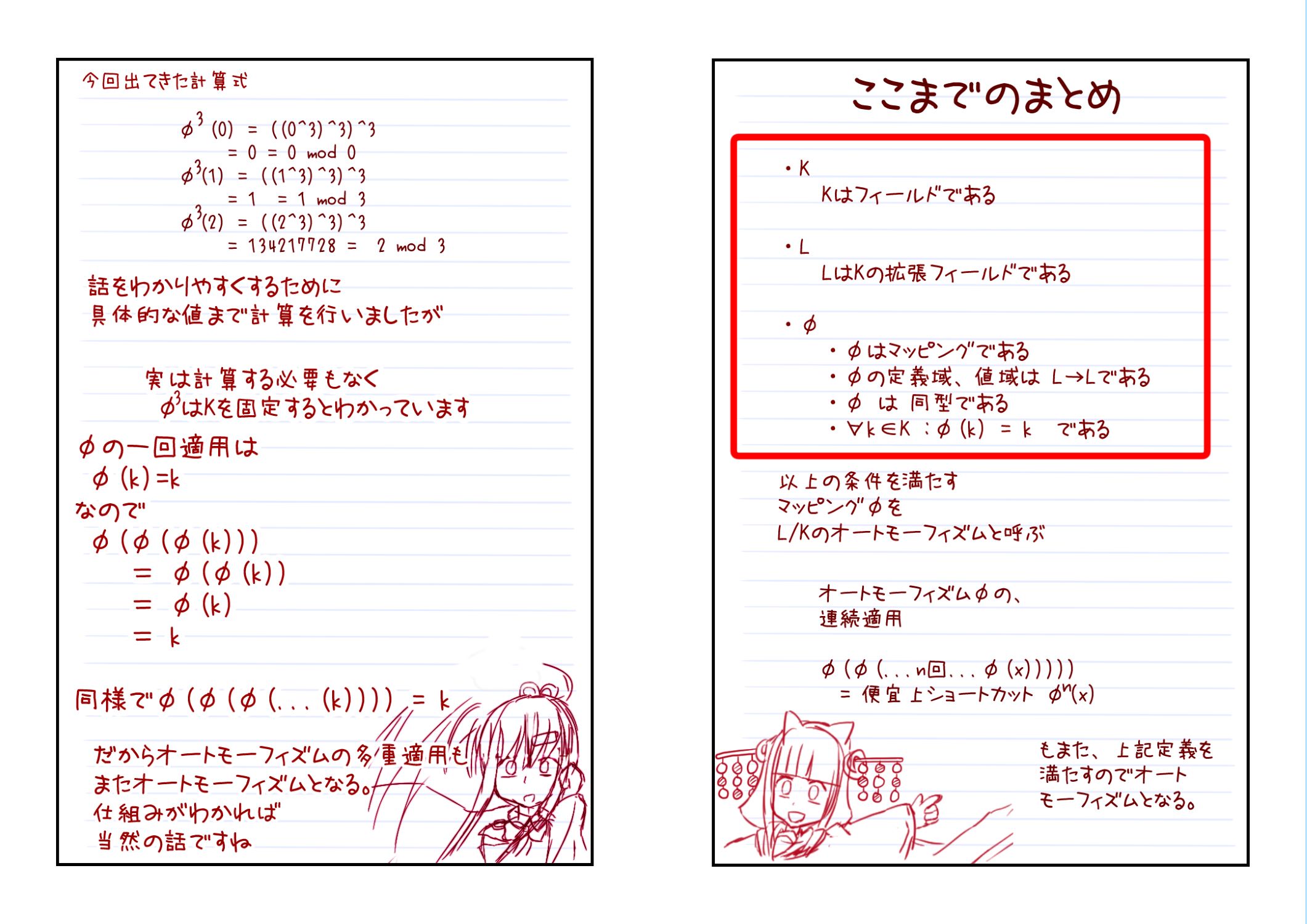
17角形とガロア理論 第16章 Autグループ

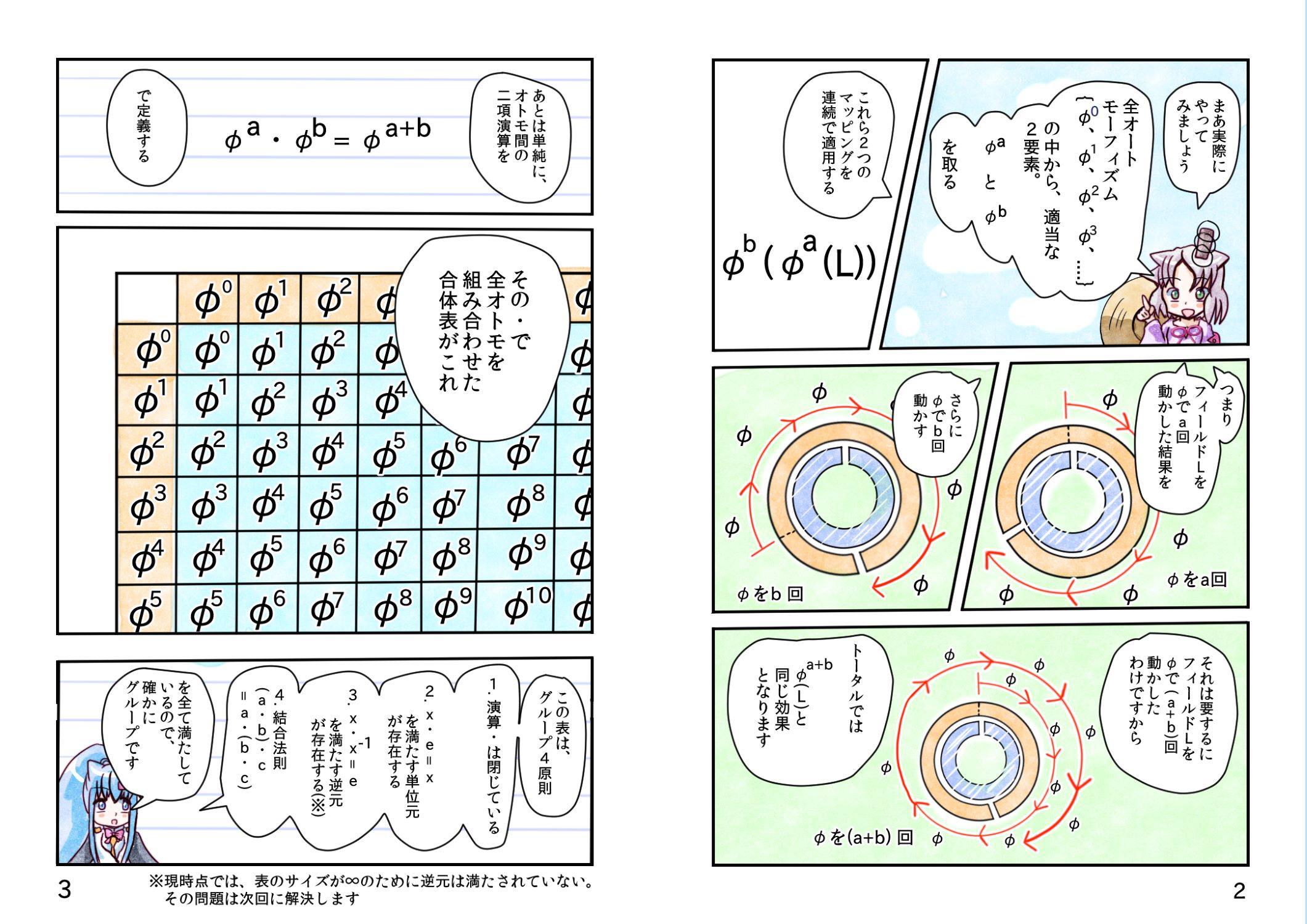

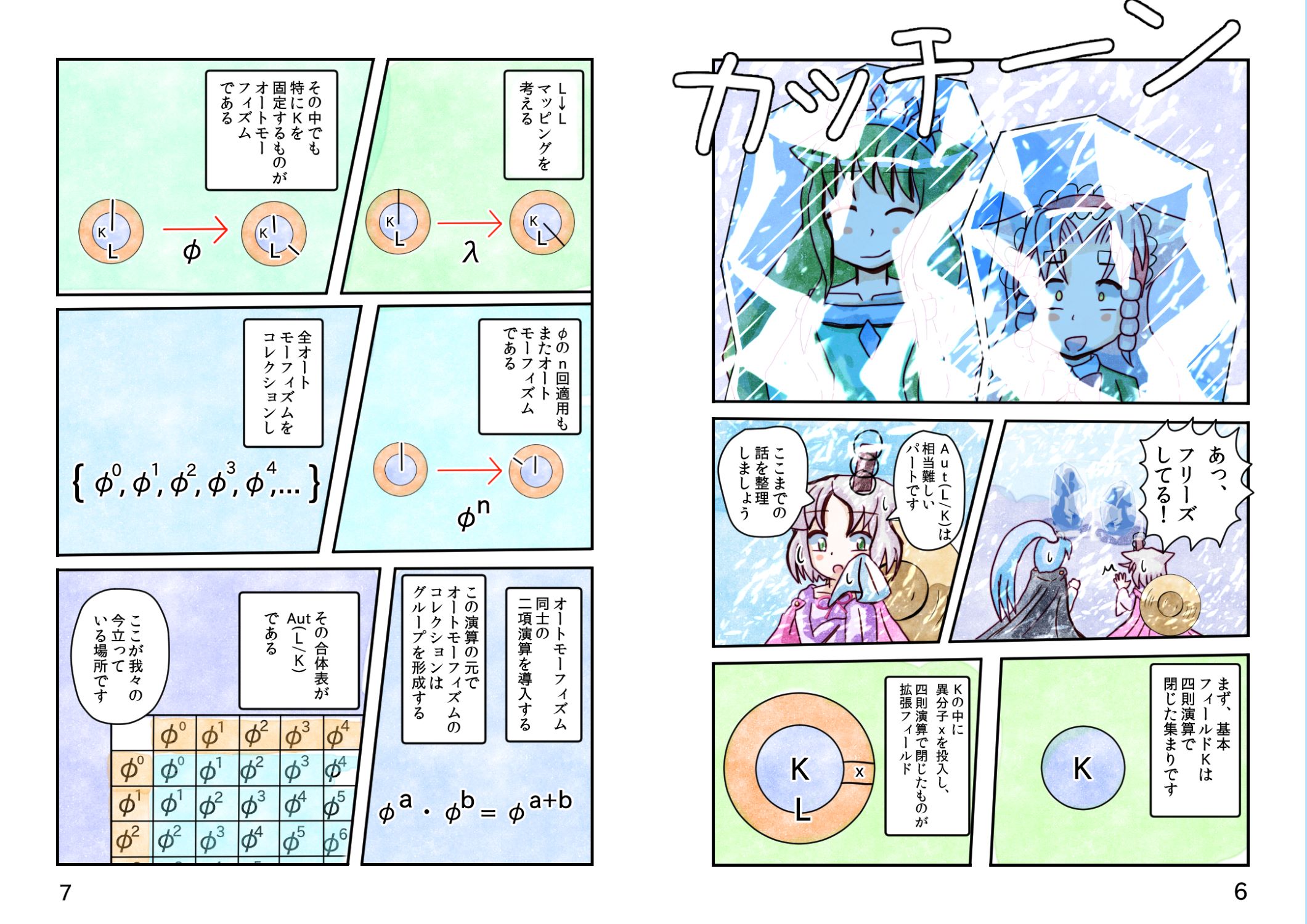


17角形とガロア理論 第17章 有限Aut

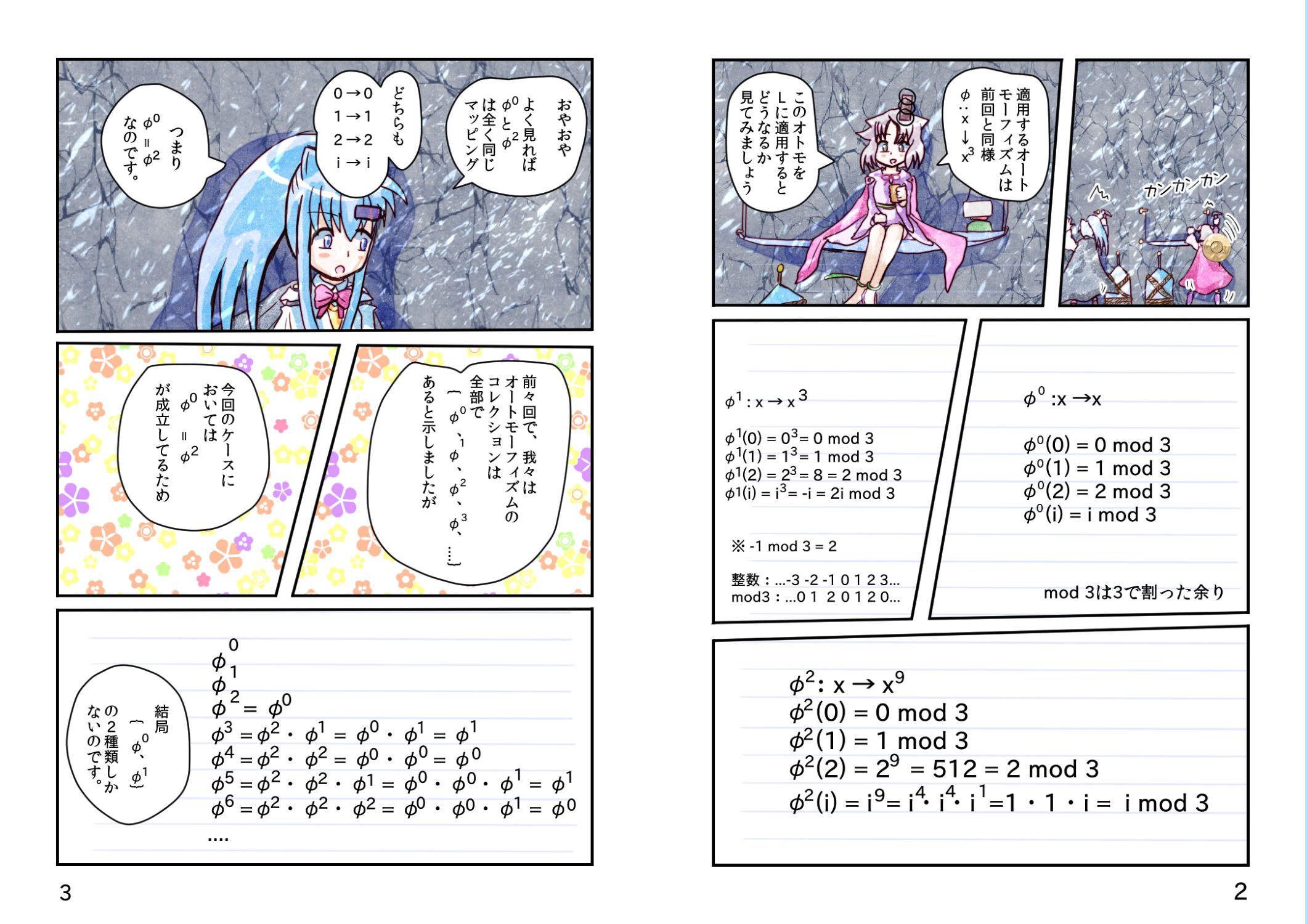

17角形とガロア理論 第18章 上流ウォッチ