「ルベーグ積分と、... 第22章 測度論の誕生 (2024/06/10)」
更新が遅れて申し訳ありません。
ルベーグ積分と、面積の測れない不思議な図形達
第22章 測度論の誕生

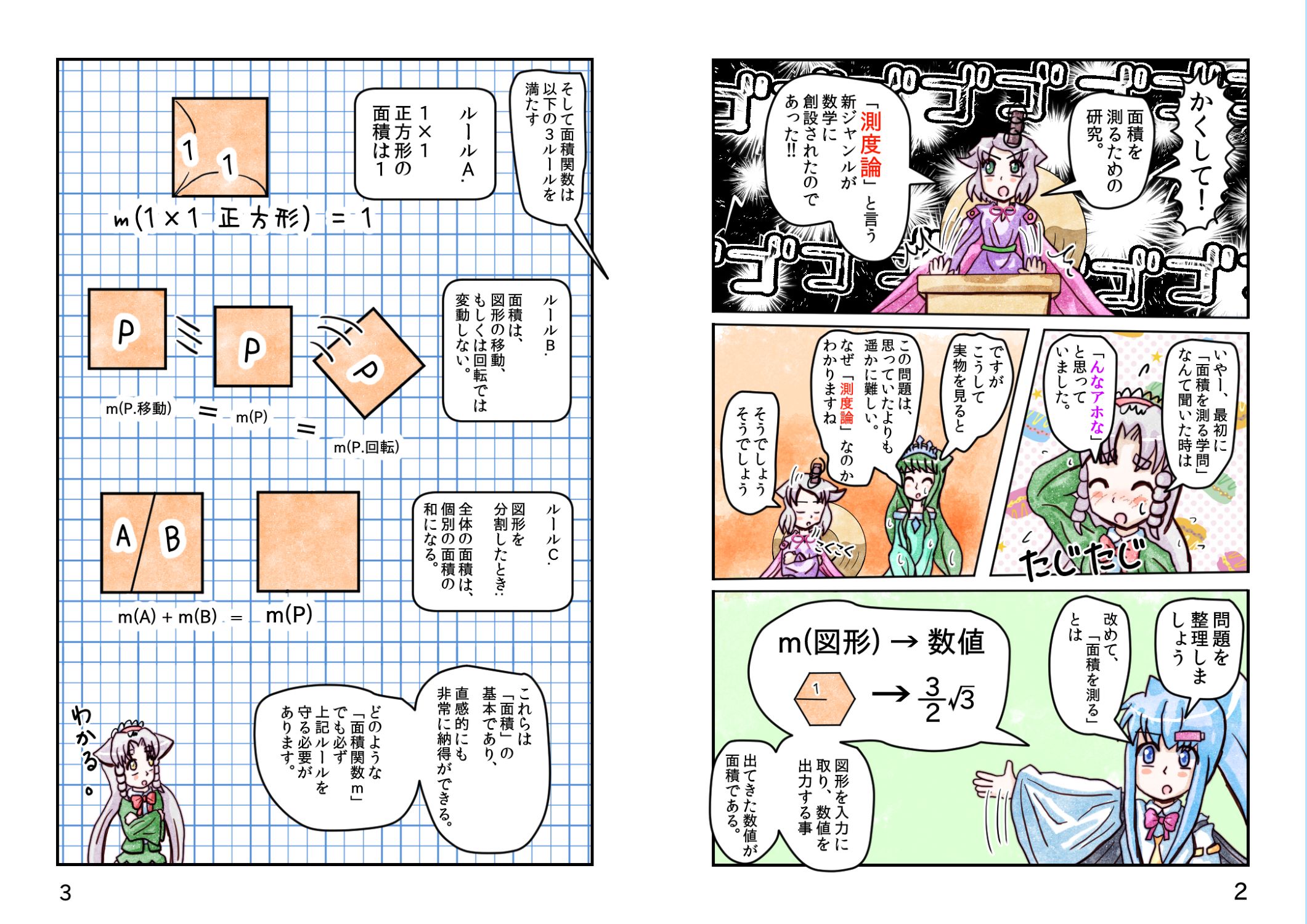

かくして。面積を測るための学問。
測度論
が誕生したのであった。
さて読者の皆様も、
ルベーグの辿った道筋。
奇妙な図形
Q : {0≦x≦1 , 0≦y≦1 , xは有理数 , yは有理数}
有理数とは、a/b (aとbは整数)として記述できる数。
無理数とは、a/b では記述できない数 (例:√2、√3、Π,e など)。
の面積を正しく測れる、
面積関数:
m'(Q) = Qの面積
の作成にトライしてみてください。