「数学パズル ボルツァーノのパズル （2023/08/05)」


さて、数学パズルをしましょう。


（ハイネ＝ボレルちゃんの初登場時の絵です・・・）


数学においては
　　ボルツァーノ＝ワイエルシュトラス (Bolzano-Weierstrass)の定理
　　　　 ‘every bounded sequence has a convergent subsequence’.
　　(あらゆる有界なシークエンスは、
　特定の値に収束するサブシークエンスを持つ)
と呼ばれる定理があり。




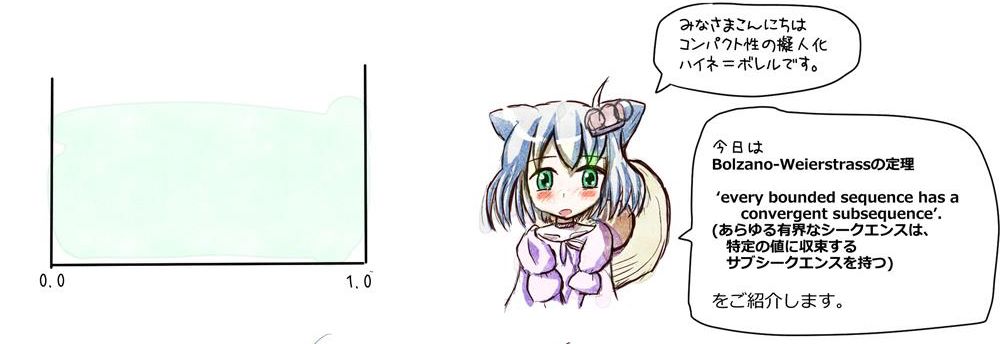
それによれば、

・[0.0] ～[1.0]の水槽の中に、
∞個数の実数を放り込めば：




→　水槽のもっと狭い区間
　　　　[α,β] (α＜β)
　　の中にも∞個の実数が存在する。
　　
　　そのような区間[α,β]が絶対にある。



→　しかも 区間[α,β]の幅はいくらでも狭くできる。


このような結果が導かれます。


さあ、なぜでしょうか？



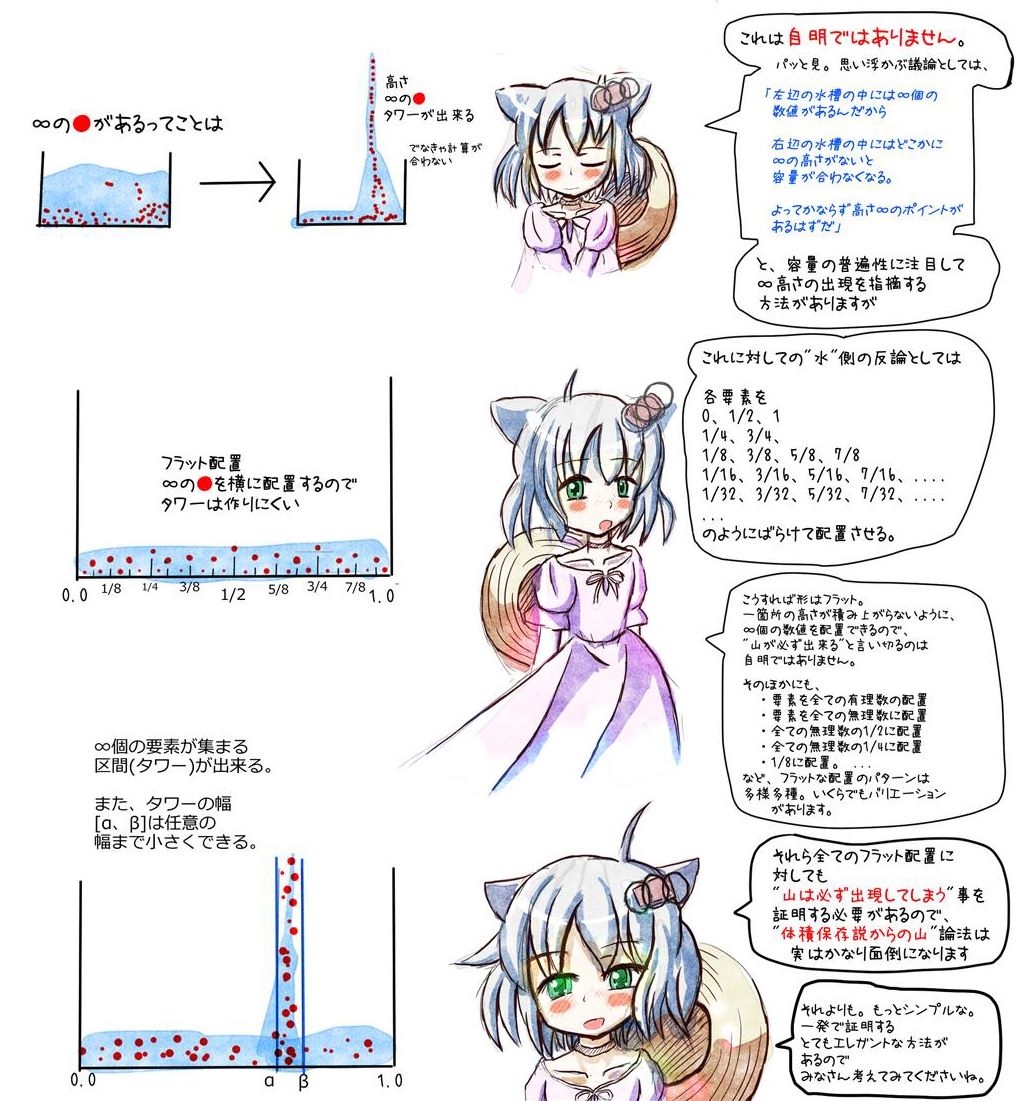
これにはとてもエレガントな証明方法。

　「あー、そっかーーーー！」
と思わず叫んでしまう
スバラシイ方法があります。