「セキュア・パズル 第8章 RSA暗号 証明編2 (2023/04/22)」
デジタル・セキュア・パズル
第8章 RSA暗号 証明編2


ほいほい。
我々は今。
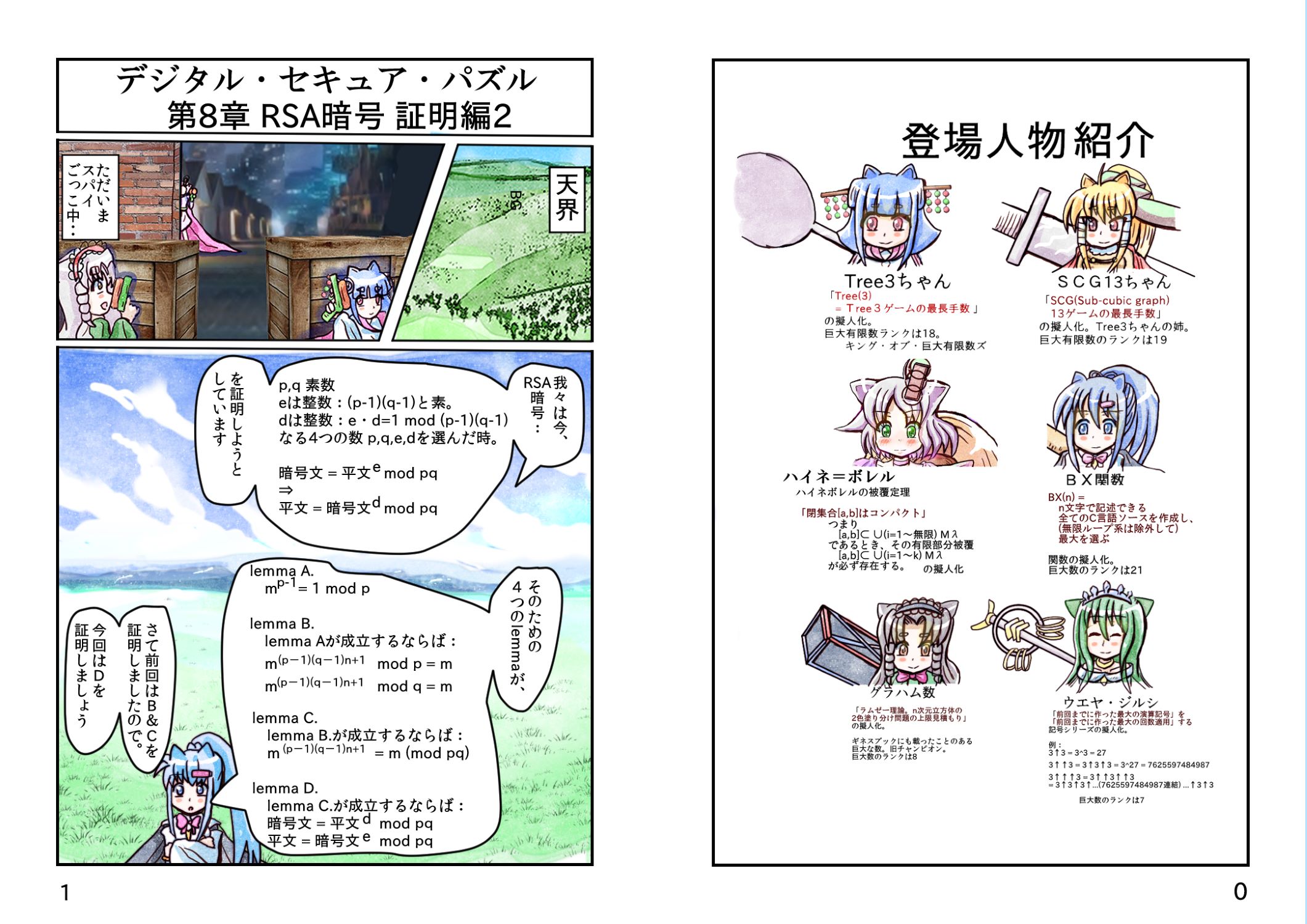
RSA暗号を4つのLemmaに分割して
lemma A.
mp-1 = 1 mod p
lemma B.
lemma Aが成立するならば:
m(p−1)(q−1)n+1 mod p
= m
m(p−1)(q−1)n+1 mod q
= m
lemma C.
lemma B.が成立するならば:
m(p−1)(q−1)n+1 = m mod pq
lemma D.
lemma C.が成立するならば:
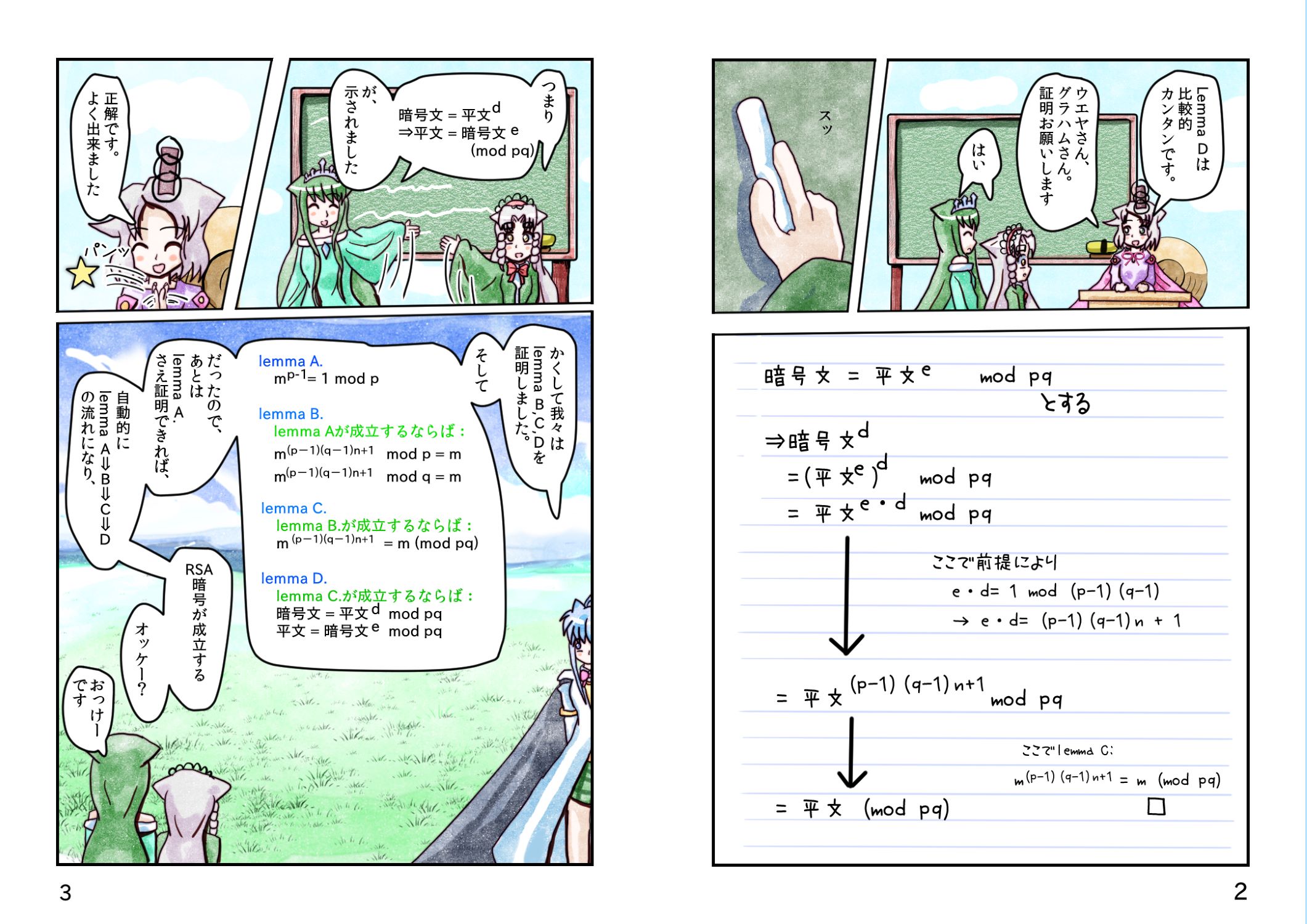
暗号文 = 平文e mod pq
平文 = e暗号文 mod pq
※lemmaとは、"命題を証明する為の小定理"。
mp-1 = 1 mod p
lemma B.
lemma Aが成立するならば:
m(p−1)(q−1)n+1 mod p
= m
m(p−1)(q−1)n+1 mod q
= m
lemma C.
lemma B.が成立するならば:
m(p−1)(q−1)n+1 = m mod pq
lemma D.
lemma C.が成立するならば:
暗号文 = 平文e mod pq
平文 = e暗号文 mod pq
※lemmaとは、"命題を証明する為の小定理"。
証明中です。
今回はLemmaDと、LemmaAのヒントをやってゆきます。