「17角形とガロア理論 第38章 17角形の作図法 (2022/10/29)」
17角形とガロア理論 第38章 17角形の作図法


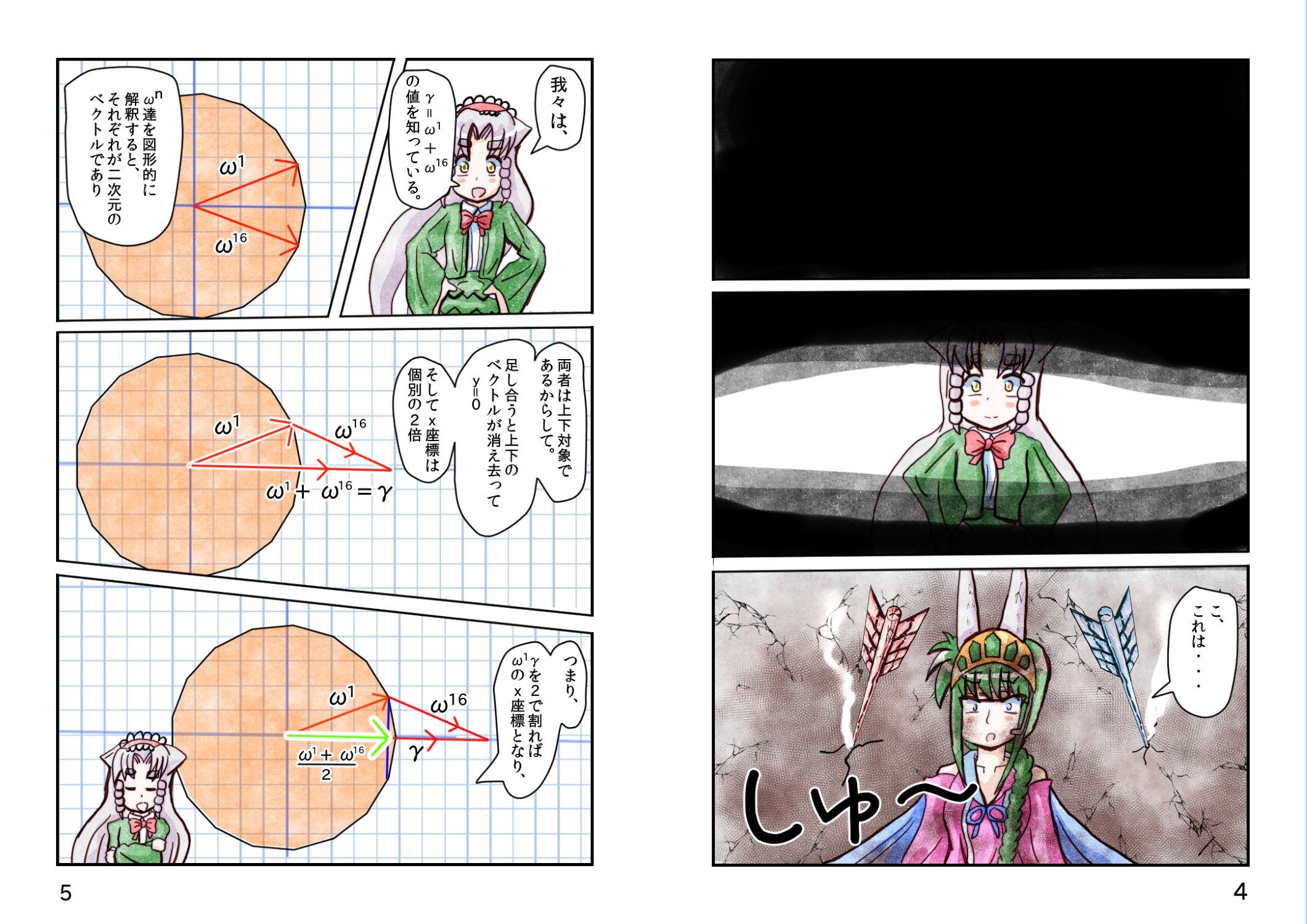

ファイナル・ソリューション。
γ/2 = cos(2π/17) = (β+√(β2 -4β'))/4
β =(α +√(α2 + 4)) / 2
β' =(α' + √(α'2 + 4))/2
α = (-1 +√17)/2
α' = (-1 - √17)/2
それぞれの項目はたかが
整数 ・ √ ・ 四則演算
で構成されているので、
あとは一つ一つの数を
定規とコンパスと作ってゆけば
確実に作図できるのがわかります。
作図gif
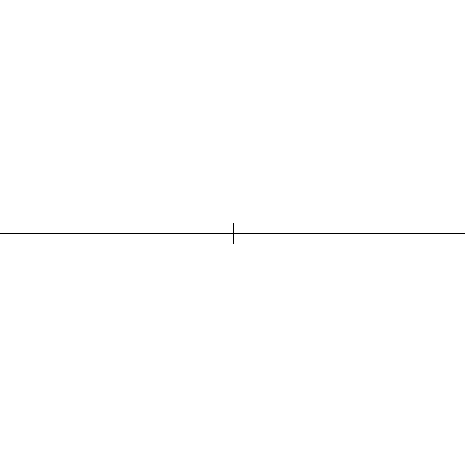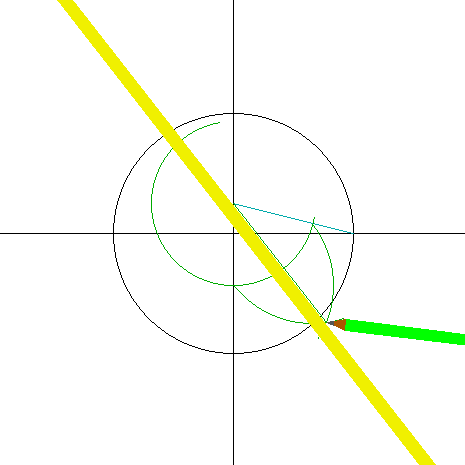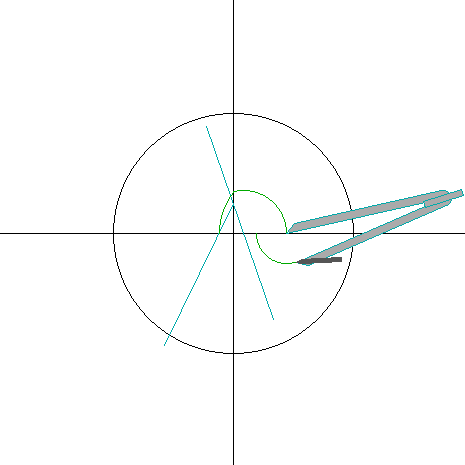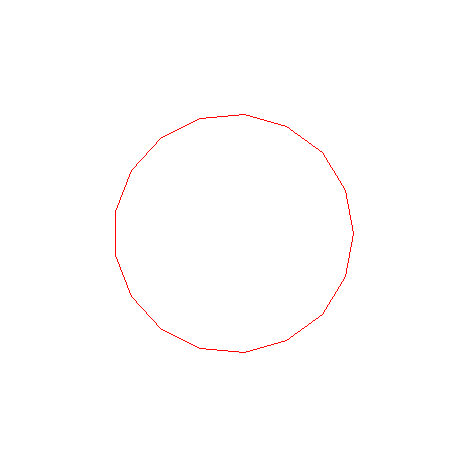
・・・このgifはネットの拾い物。
私が作った物ではないので
γ/2法とはちょっと違いますが、^^A;
やってる事は本質的には同じです。
α → β → γ。補助線を引きながら
段階的に複雑な数を構築してゆき、
1/17ピースを作図。
最後はピースを増殖してゆけば
17角形が完成します。
ユークリッドによる幾何学の創設。西暦-300年から
西暦1796年。ガウスによる作図法の発見まで
実に2000年間の間。
人類は
17角形は(定規とコンパスでは)作図できない。(だって素数だから)
と間違った思い込みをしていましたが。
実は作図できるのです。本当に。
ちなみに17角形の作図法を発見したガウスさえも、
「なぜ17角形は作図できて、13角形や19角形は作図できないのか」
その仕組み自体は
知らたかったみたいですが。
その仕組みを、完璧に説明できるようになったのが
ガロア理論であり。
グループ/フィールド/オートモーフィズム/ガロア補題/ガロア理論
を動員した、極めて高度な
数学的メカニズムが働いていたのです。