「17角形とガロア理論 第35章 なぜ解けるのか2 （2022/10/08)」

17角形とガロア理論 第35章 なぜ解けるのか2

---

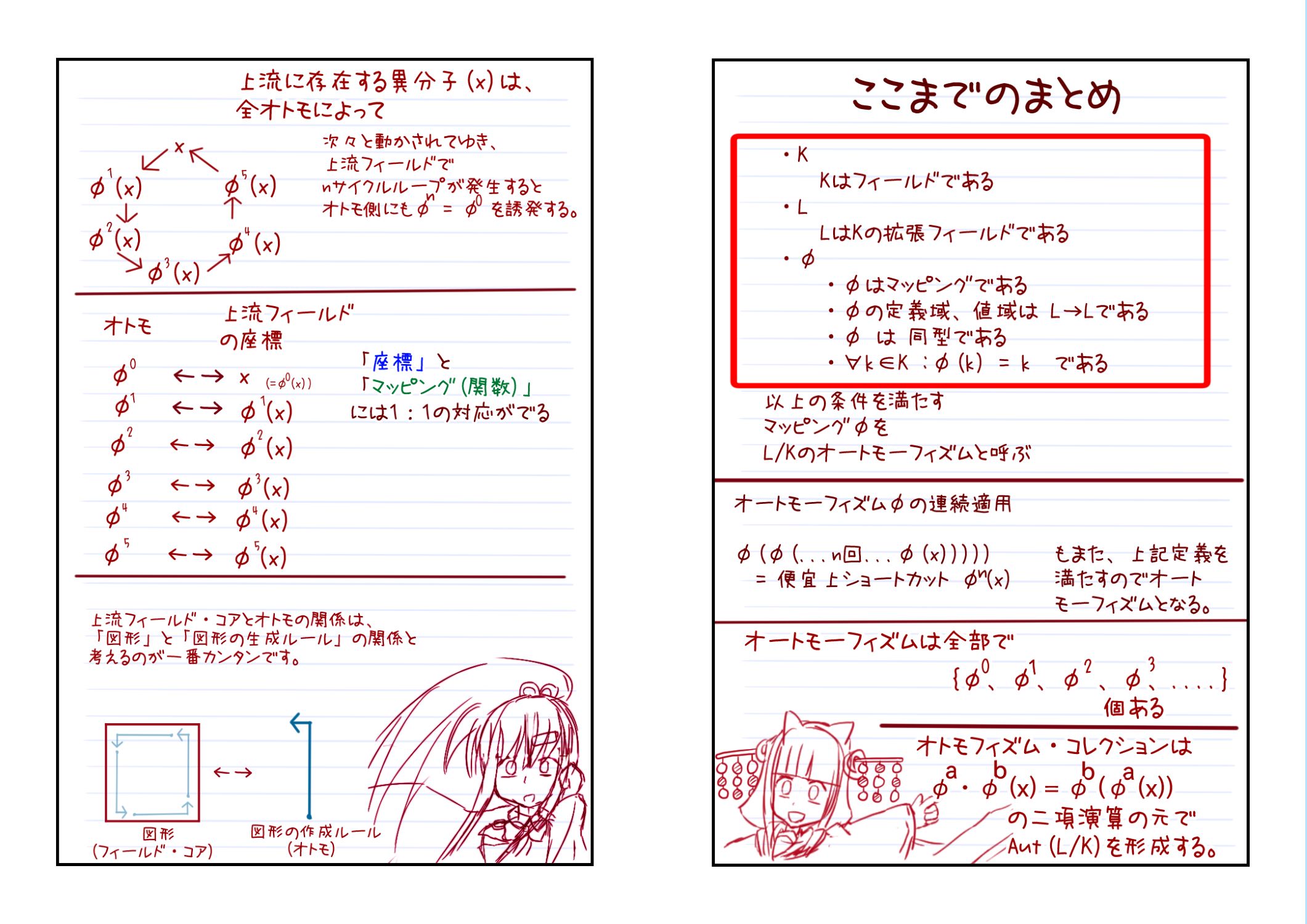
なぜ、17角形は作図できて。
13角形や19角形は作図できないのか。

13と17と19。
全て素数なのにどこに違いが出るかと言いますと。

---

17角形は
　　17角形 → コア要素16個 →　オトモ16個 → AutはG16

これが
　　G16 →　G8　＋　φG8
　　G8 →　G4　＋　φG4
　　G4 →　G2　＋　φG2
　　G2 →　G1　＋　φG1

一段一段がペア分解。
→　未知数は2つ、uとvの連立方程式が出現
→　未知数2の連立方程式を解く過程で2次方程式

これしか出ないから、
全部√で記述できる数が出てくる。

それが根本的な理由です。

---

一方で13角形や17角形などは
　　13角形 → コア要素12個 →　オトモ12個 → AutはG12

　　G12 →　G6　＋　φG6
　　G6 →　G3　＋　φG3
　　G3 →　G1　＋　φG1 + φ²G1

どこかに必ずトリオ分解が出てくる
→　未知数は3つ、uとvとtの連立方程式が出現
→　未知数3の連立方程式を解く過程で3次方程式

そして、3次方程式を解く過程で3乗根。

例えば
　　2 ^1/3
のような定規とコンパスでは作図できない数が
出てくるから、
13角形は作図できない。

---

ユークリッドの時代（西暦-300年）から、
ガウスによる17角形の作図法の発見(1796年)まで。
実に2000年もの長い時間 。

人類は
「17角形は作図不可能
　　　(だって素数だから)」
と、間違った思い込みをしていましたが。


実は、17 角形
この"17、素数"の部分は
作図可能性とはあまり関係がなかった。^_^A;

「n角形-1」のAutグループの構造の方が、
作図可能性を決めていたのです。

---