「ハイネ＝ボレルの被覆定理 （2022/03/12)」


今週の「17角形とガロア理論」はお休み～。

やってる内容はガチガチの数学理論で、
だいぶハードになるので。
定期的に息休めを入れます。


さて、今回はハイネ＝ボレルちゃん


の初出を振り返ります。


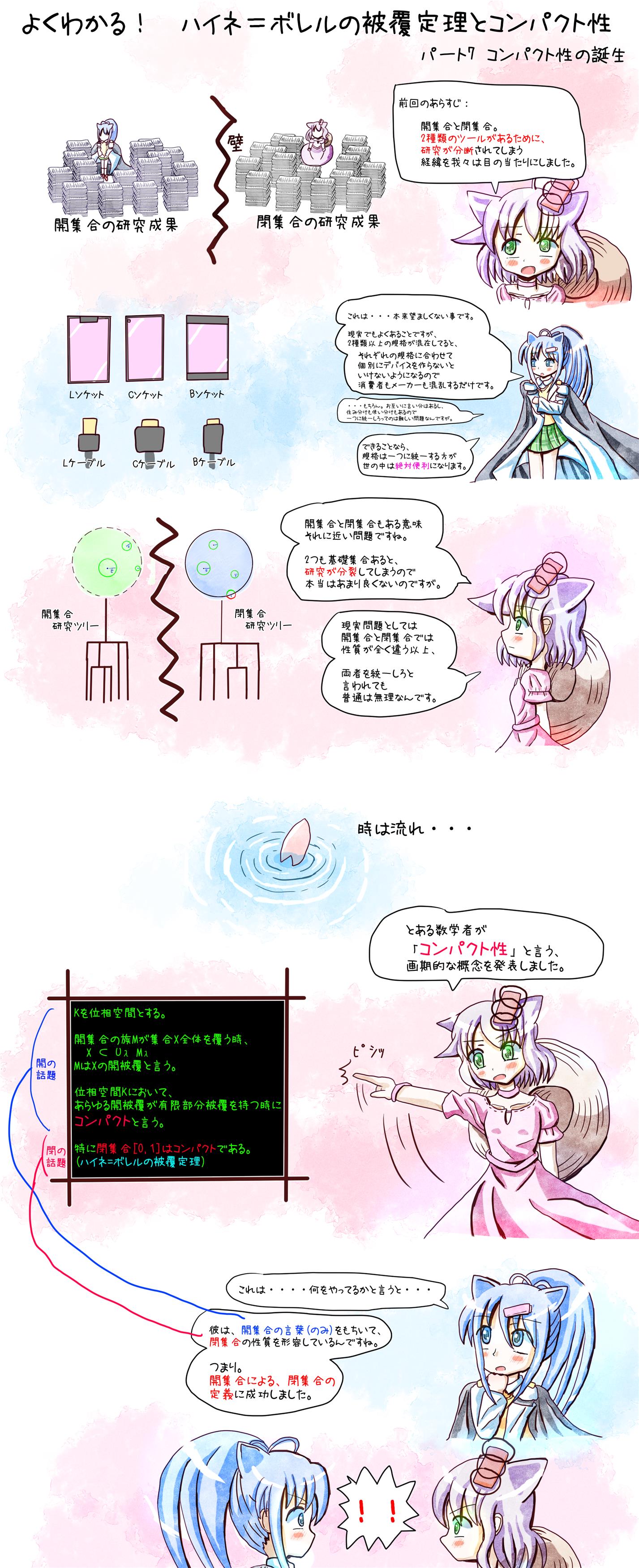
元々は、数学におけるコンパクト性
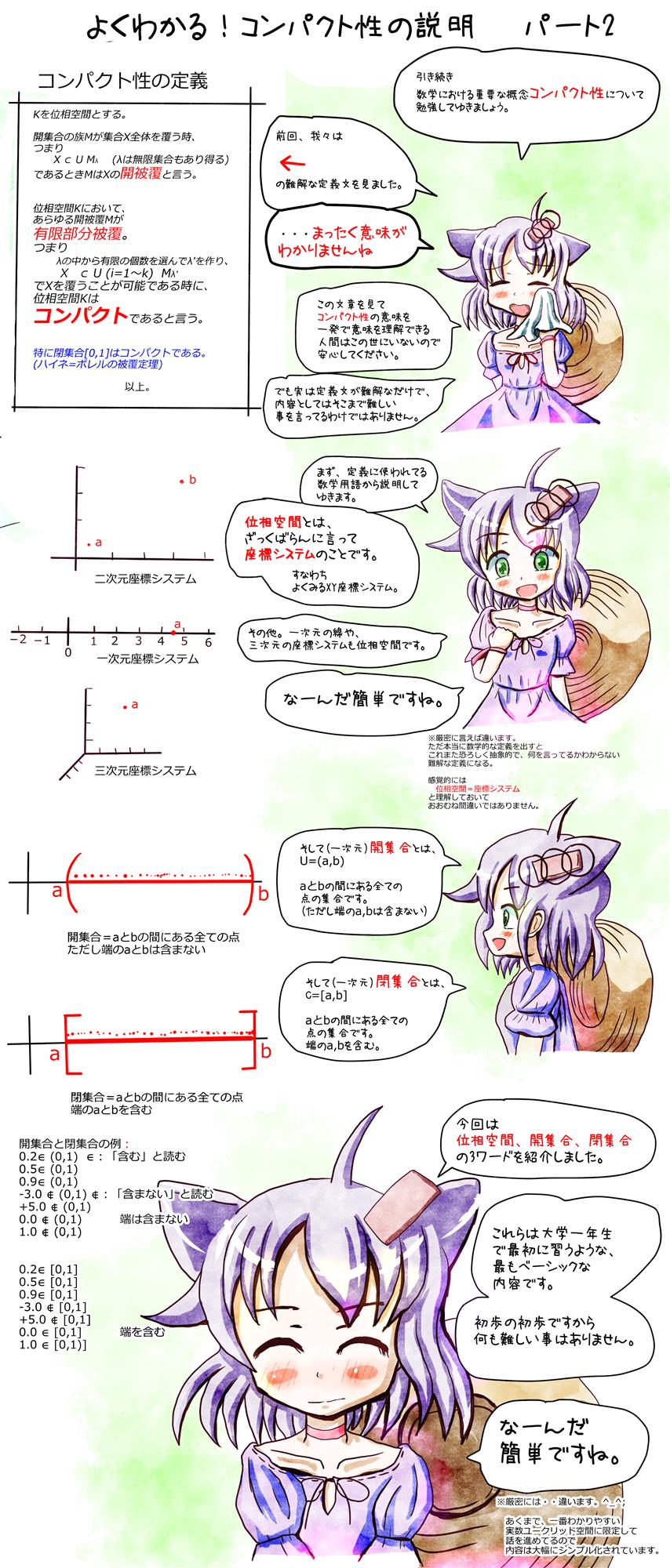
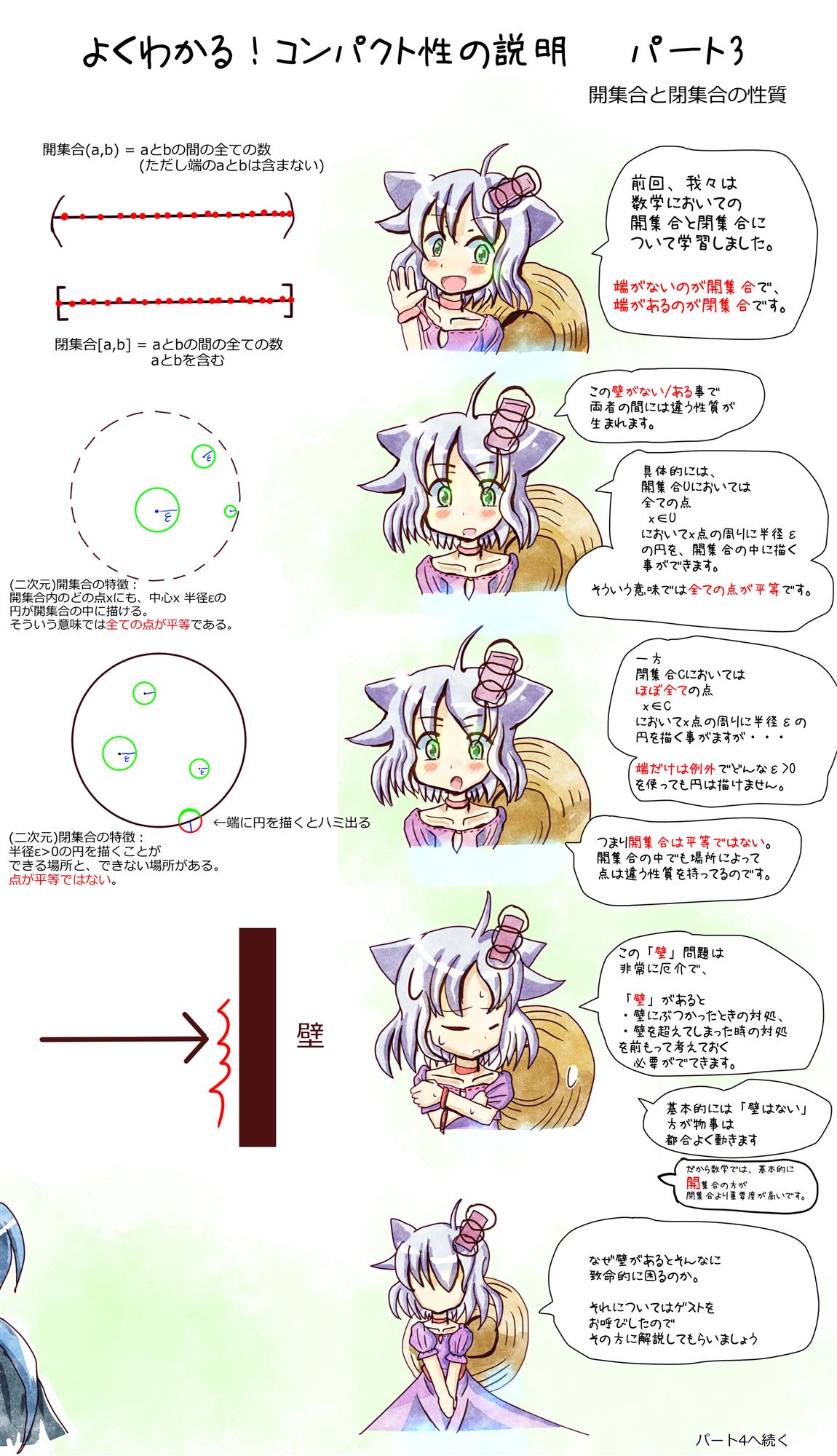
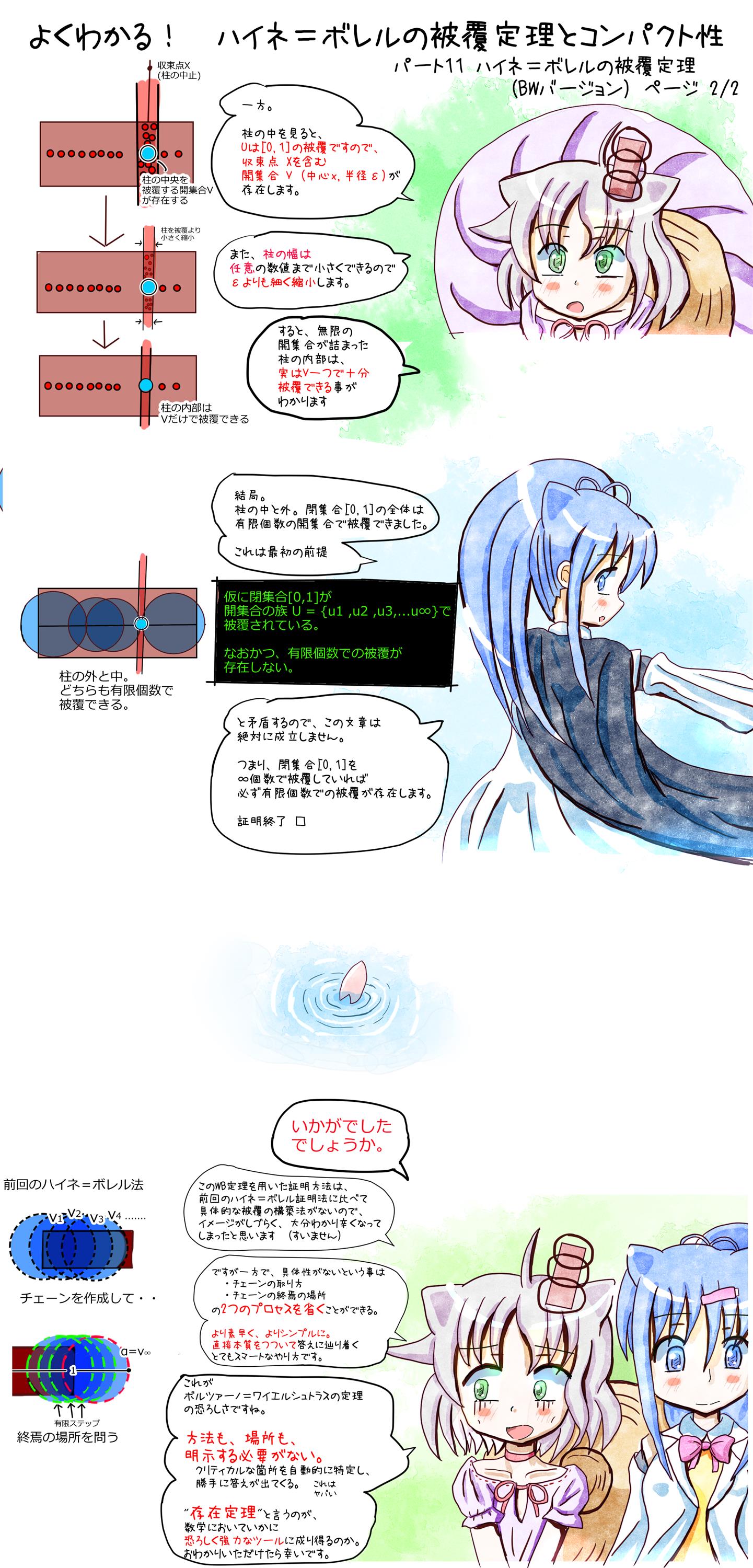
Kを位相空間とする。

開集合の族Mが集合X全体を覆う時、
　　X ⊂ UλMλ
MはXの開被覆と言う。

位相空間Kにおいて、
あらゆる開被覆が有限部分被覆を持つ時に
コンパクトと言う。

・・・・何言っとるか。ぜっんぜん意味がわからん！

コンパクト性は、数学の
あらゆるジャンルで出てくる
重要な概念なのですが。


定義を教えられた所で、絶対に意味がわからない。
怪文章として有名な定理なんですわ。^_^;

これの擬人化からやってきました。


以前やった内容





























　被覆定理！



ってな事が昔ありまして。

理論方面に結構強そうなので、
今回の「17角形の作図問題とガロア理論」の
講師役をお願いする事にしました。


衣装は2022年版。
講師にグレードアップしたのに
合わせてちょっと変わっています。