「17角形とガロア理論 第03章 色々なグループ (2022/01/15)」
色々なグループを見てゆきましょう。

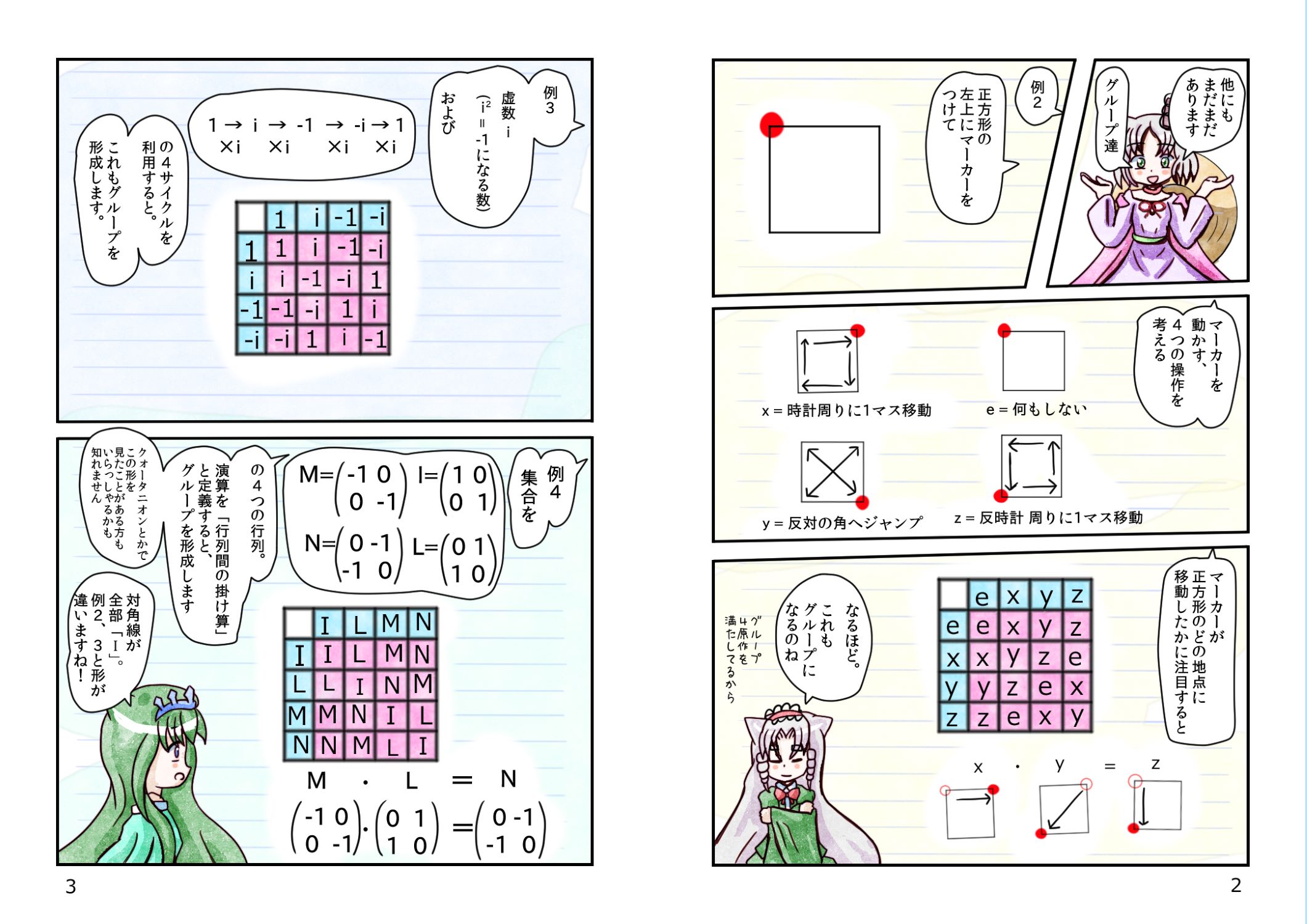
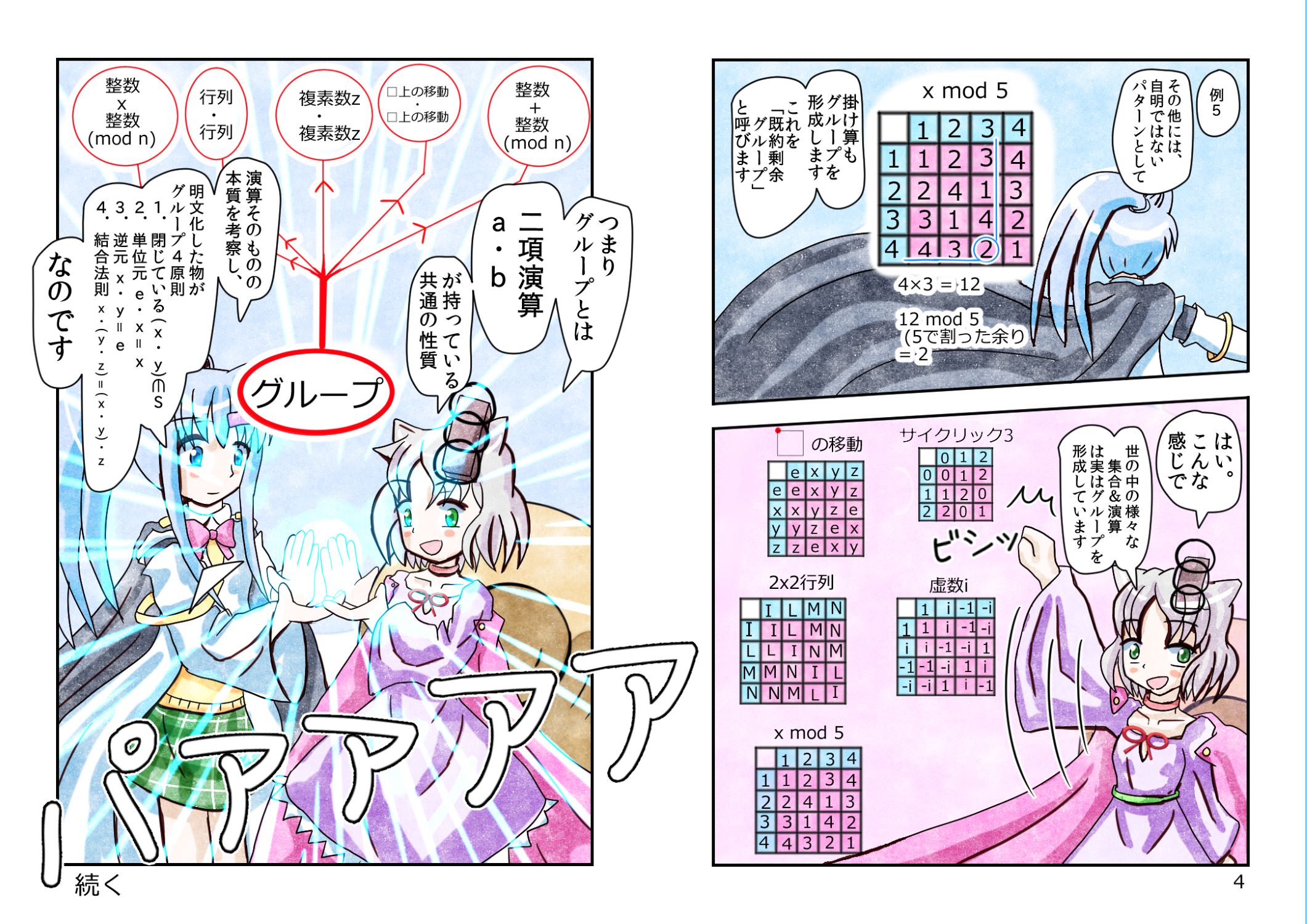

グループとは、つまり
整数+整数
整数×整数
複素数×複素数
移動・移動
行列・行列
など。
あらゆる
a・b
に共通する要素を、
注意深く観察して
抜き出した物です。
全ての二項演算
a・b
に共通する法則であるがゆえに。
グループは、特定の単位(整数 / 複素数 / 行列など)
を持たない「無単位の法則」である。
この無単位性があとあと。
フィールド / フィールド = オートモーフィズム グループ
の考えに重要になってきます。
(なぜなら分子のフィールドと分母のフィールドが単位を消し合うので、結果は無単位となり
そこでグループが出てくる)
結局の所この
オートモーフィズム グループ
なるものが17角形の作図問題とガロア理論の本質であり、
絶対に知っておかなくては
ならない事柄なので。
我々は今。
グループの基本理論を学んでいるのです。