「17角形の作図問題とガロア理論 (2022/01/02)」
新年数学コラムをします。
今年のお題は・・・・
17角形の作図問題とガロア理論


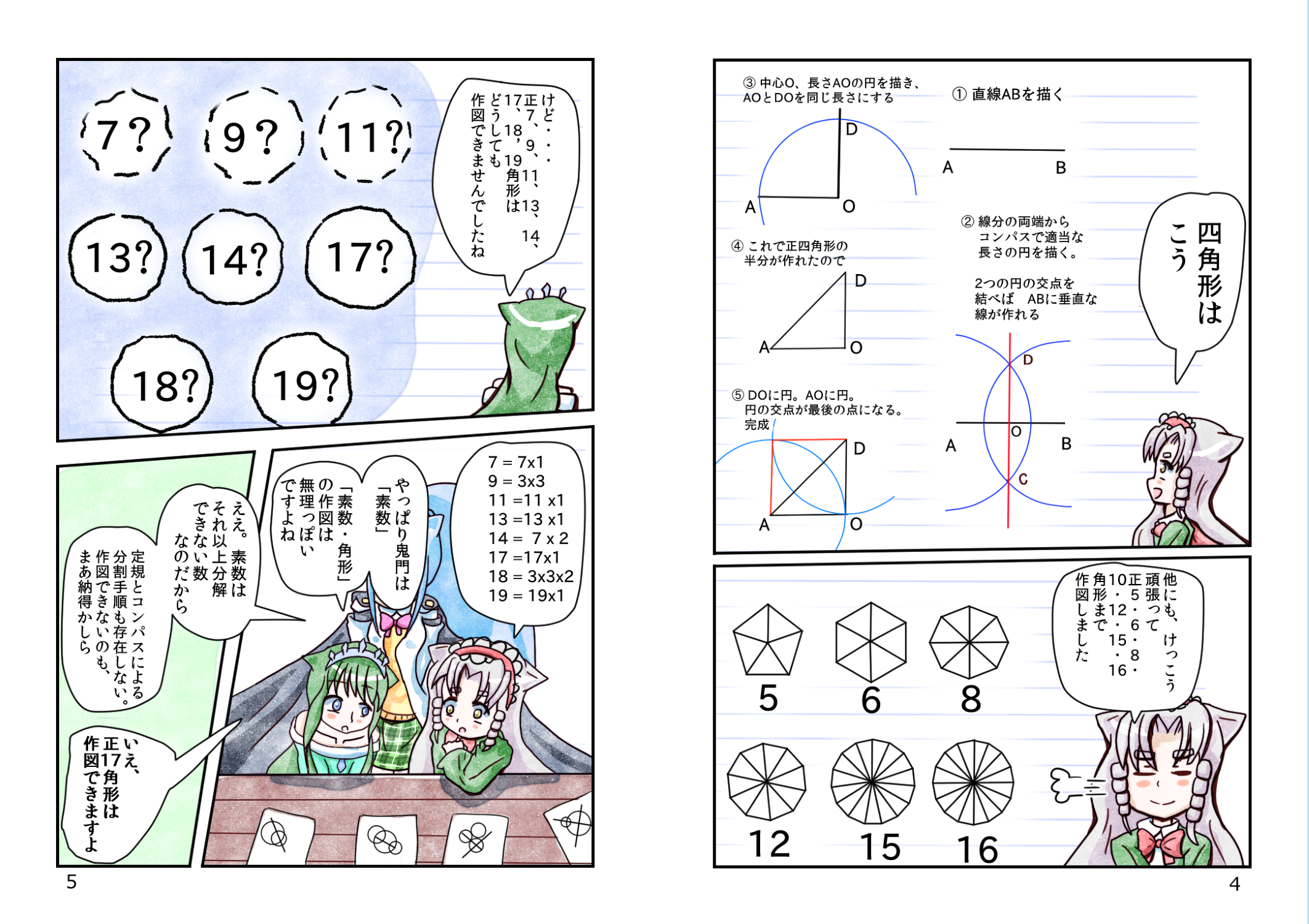


コンパスと定規だけで様々な図形を作成する
作図問題は、紀元前から存在していて。
当時からすでに
3・4・5・6・8・10・12・15・16・20...
角形は作図法は発見されていました。
その一方で
7・9・11・13・17・19...
角形。特に素数・角形は「作図不可能」とされていました。
これは実に西暦-300年 ~ 1700年。
2000年の間も数学者達の間でも
ずっと信じられていた学説。
「素数・角形は作図できない」と、誰も疑わなかったのですが。
ドイツの数学者ガウスが、
1796年になんと
17角形の作図法を発見してしまいます。
・・・実は17角形は作図できたのです。
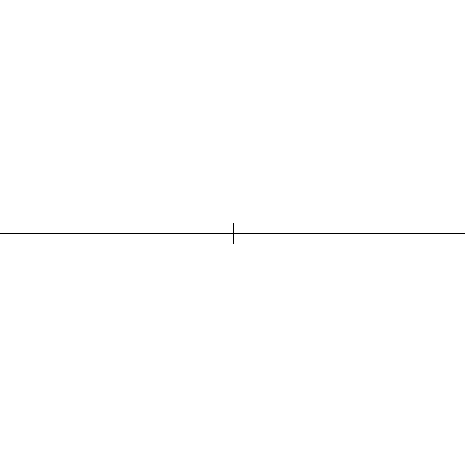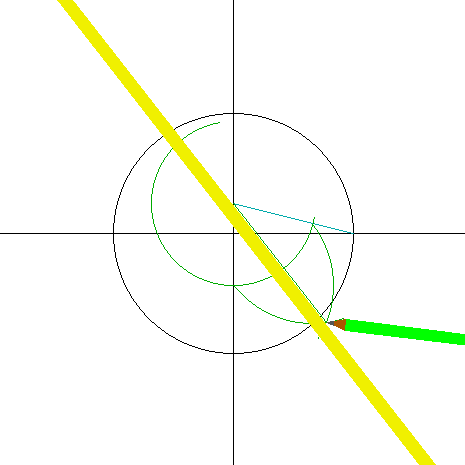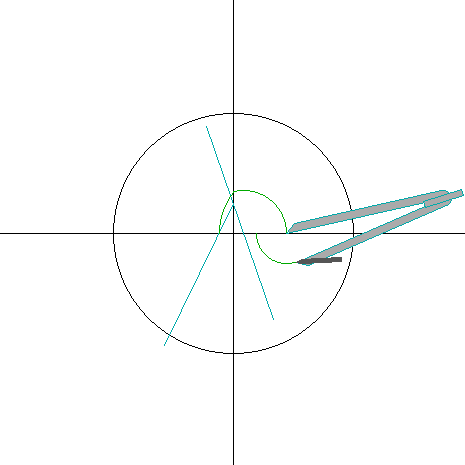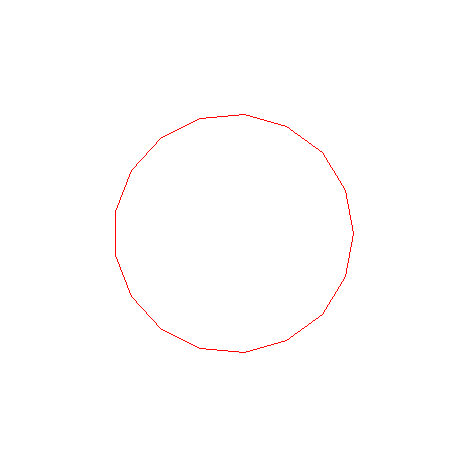
その一方で、13角形や19角形は相変わらず作図不可能で、
(正確に言えば誰も作図法を見つけられなかった)
なぜ「素数17角形は作図可能」なのに、
「素数13・19角形は作図不可能」なのか。
作画できる物と、できない物。
何が違うかは未解明。
その謎が解き明かされたのは1830年。
五次方程式
x5 + ax4 + bx3 + cx2 + dx1 + e
の解法を研究をしていたガロアが、
ついに
五次方程式の解の√記述不可能性
を発見し、その証明メカニズムは
のちに「ガロア理論」として
知られるようになる。
そしてそのガロア理論によって、
n角形の作図可能性 / 不可能性
も説明・証明できるのです。
本稿では、これを解説して
ゆくことになります。
実に、解くのに300年かかった(研究開始 西暦1500年~ 証明発見1800年)
ウルトラ超難問です。
さすがに・・・これは難しい。^_^;
「ガロア理論」の習得難易度は
高校数学 IIIよりも上です。
(あれをテスト100点取れる人間でも、まだ相当難しく感じるでしょう。)
去年やったTree3の停止性証明の30倍ぐらいかな。
今回はまあ。ハードな内容となりますが
「17角形の作図」
のみに話と議論を絞れば・・・実は結構いけるかも。
むしろ
群論・体論・自己同型写像 Aut(L/K)
への入門編。
なぜ"群論"が 現代数学においてかくも重要な役割を果たすのか
"グループ"の意味と役割と必要性を示す、
絶好の例題かなと
個人的には思います。
レッツゴー