1+2+3+・・・・ = -1-12 日記

Tree3の停止性証明第13章 Higmanの定理

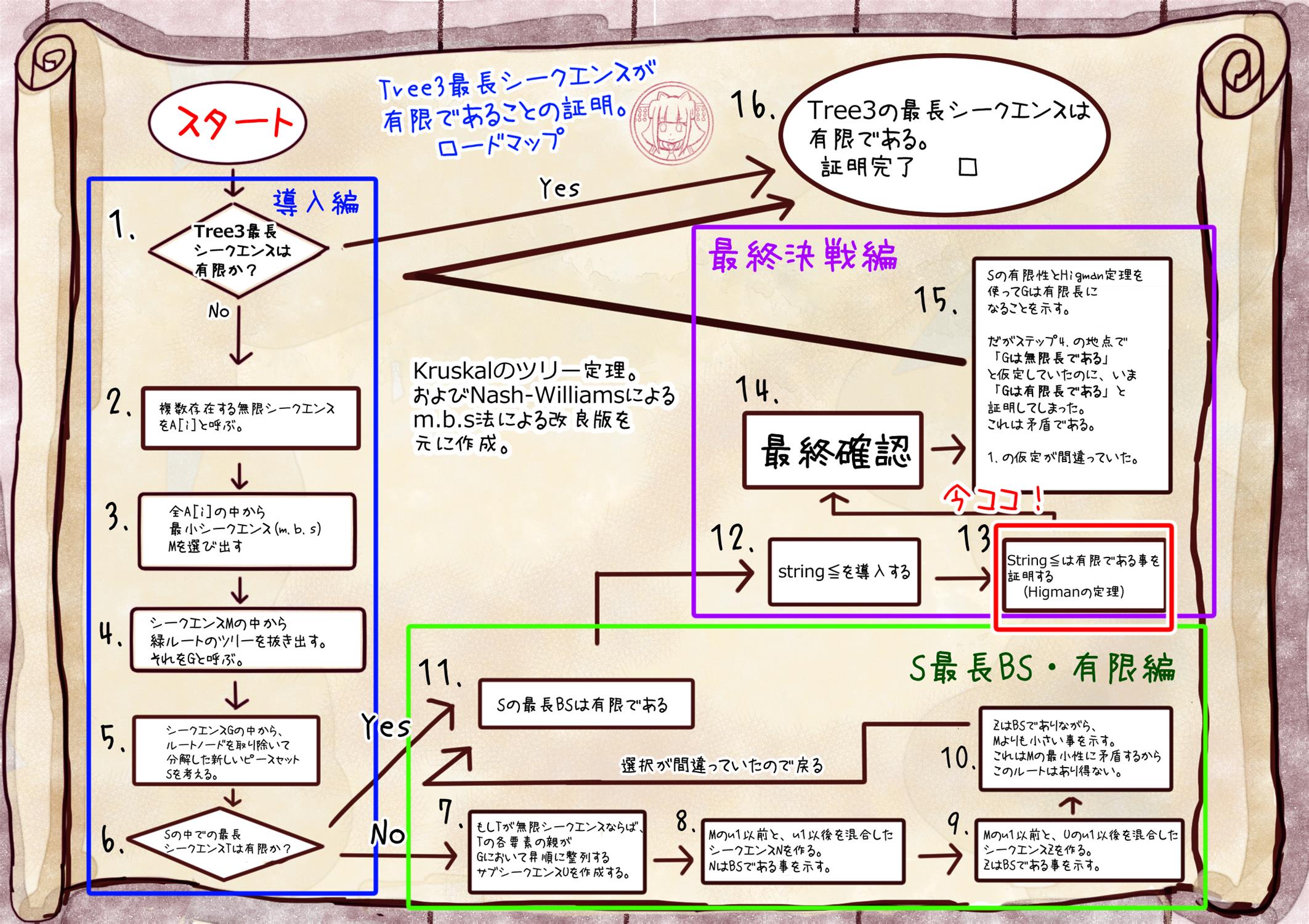
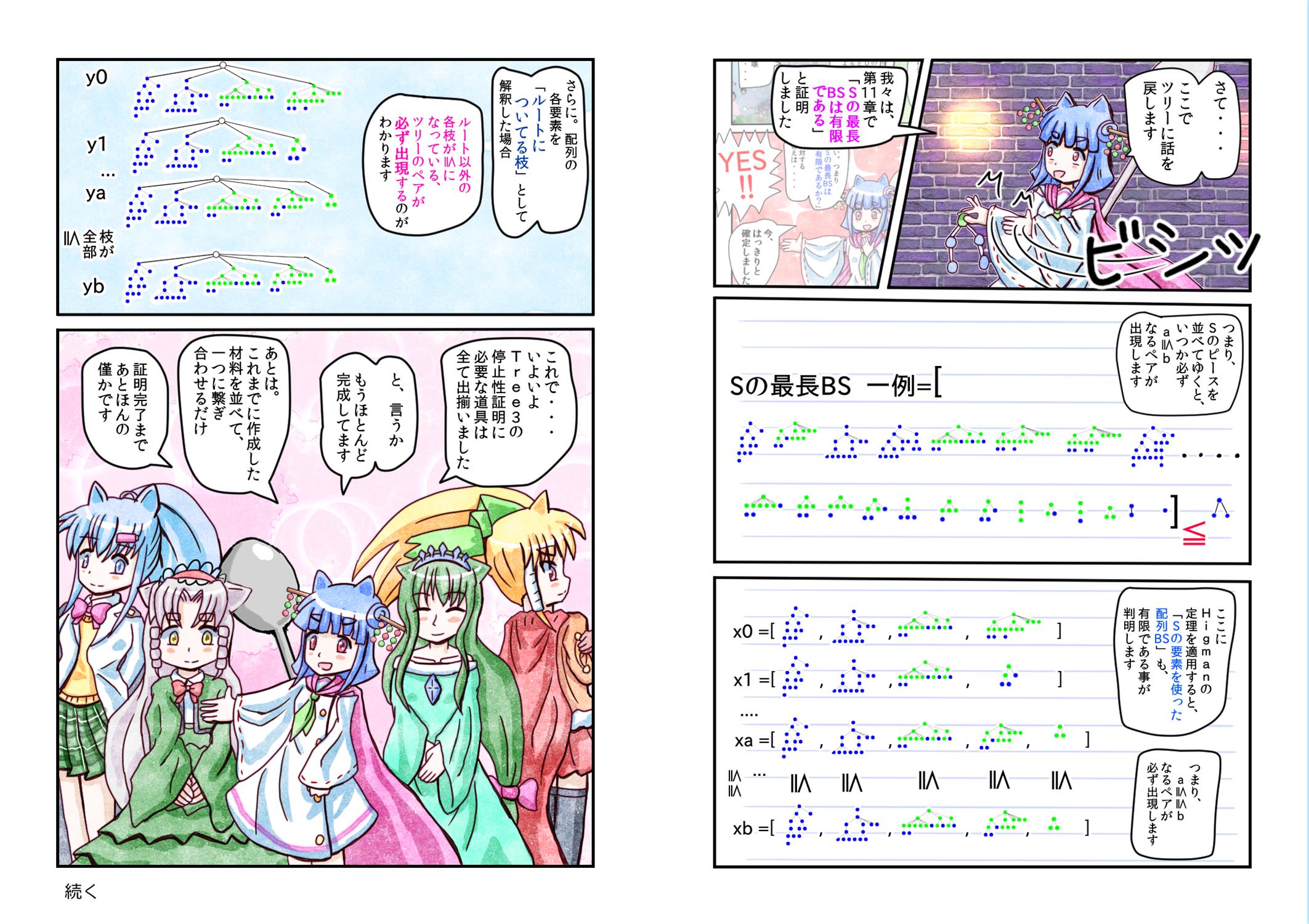
Higmanの定理。
なかなかの難問ですが、
「種明かし」さえしちゃえば
十分理解できる範疇の話だと思います。

・・・ですがその。
「種」を見つける作業が恐ろしく難しいんだ。^_^A;

Array＜int＞の停止問題を
ヒントなしの、完全に自力で解ける人間は
かなりレアです。

おそらく・・・

・大学数学専攻の生徒レベルが、
　　(大学の知識は全く使いませんが、
　　それぐらいの"証明ガチ勢"じゃないと無理)
　　
・「Array＜int＞の停止問題は1ページで証明できる」と教えられた上で、

(長さはとても重要。
答えが1ページなら、トリックはきっとシンプルで
ちょっとした気づきさえあれば
クリアできるはずだと推測できるから。
それだけですんごい大きなヒントになってる)

・1週間頑張れば

解けるぐらいのレベルだとは思います。はい。

一番重要なのは②の「複数BS、全体を見回す必要性」。
ここさえ閃いたら90％は解けたようなものです。

マンガ中ではさらっと通りましたが
こーれがムズい！

この発想は普通出てきません。

正直言うて、これを思いつくのは
ちょっと尋常じゃない。(不可能ではありませんが)

それぐらいの鬼すぎる難易度です。

次に重要なのが⑤の「左端要素だけに注目する」
ここに気づいたら99％。

残り⑥～⑯の道筋はわりと自然に出てくるでしょう。

解けそうで・・・解けないで・・・解ける。
本当に絶妙な難易度なので
数学系の人間にこの問題を見せたら

絶対にこうなります。絶対に。^_^;