「数学コラム よくわかる！コンパクト性の説明 パート11 （2020/11/14)」

ハイネ＝ボレルの被覆定理
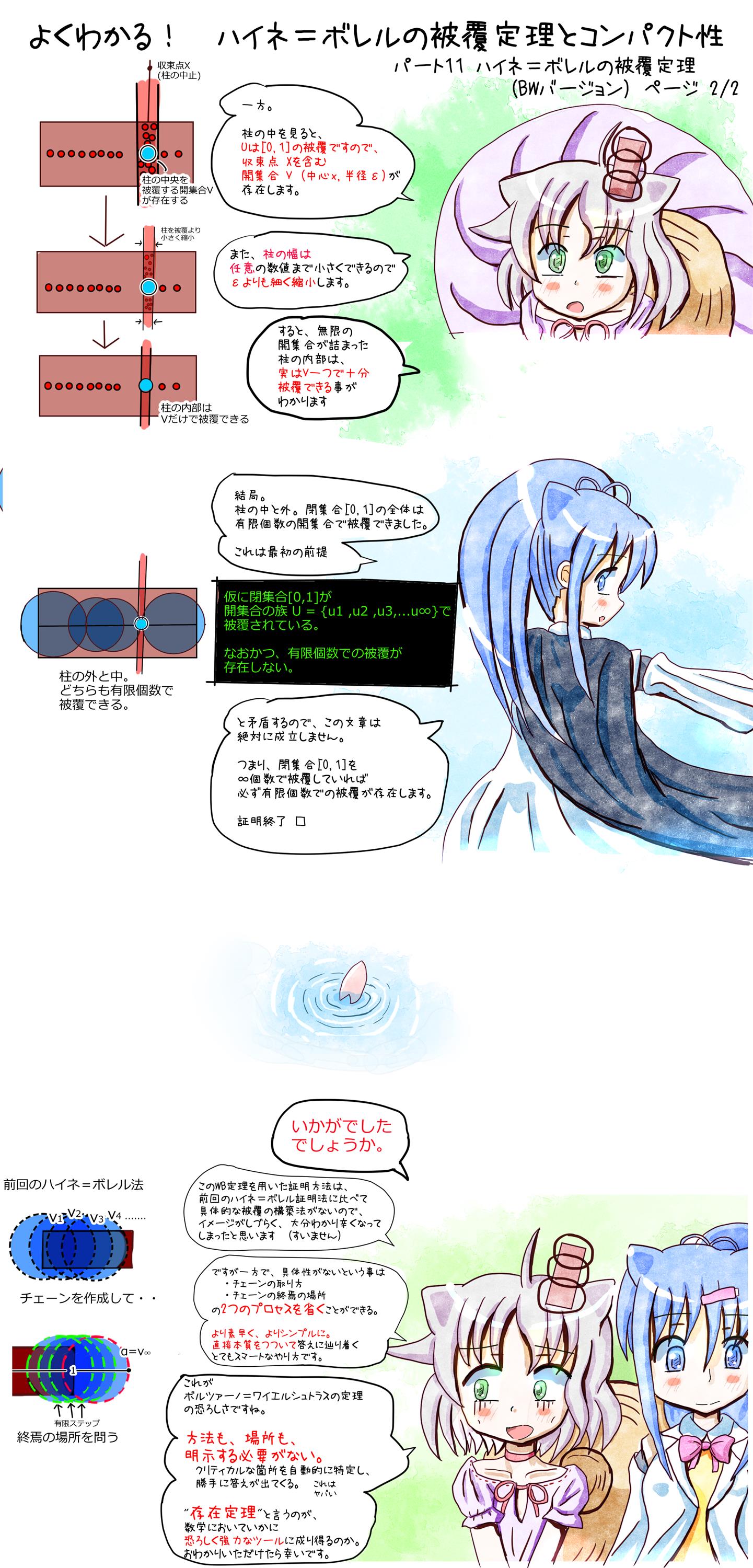
　　閉集合[0,1]はコンパクトである
を

ボルツァーノ・ワイエルシュトラスの定理
(あらゆる有界なシークエンスは
　特定の値に収束するサブシークエンスを持つ)

を使った証明を示します。

---

・・・どうでしょうかねえ^_^;

前回のハイネ＝ボレル式、純正証明と違い、
　　・チェーンの構築
　　・チェーンの終わりの場所
を使わずいきなり答えが出てくるのがこのWB証明法の特徴です。

具体的な構築手順が存在しないので
感覚的にはちょっとむずかしく見えるかも知れませんが。

逆に言えば
　　「具体的な構築手順」
のプロセスをすっ飛ばしても
答えが出てくるので
慣れればこっちの方がスマートな解法になると思います。

---

ハイネ＝ボレルの被覆定理とボルツァーノ・ワイエルシュトラスの定理
は等価です。

無限の開集合について：
　　・ORを考察したのがハイネ＝ボレルの被覆定理であり、
　　・ANDを考察したのがボルツァーノ・ワイエルシュトラスの定理。
両者は表裏一体。
コンパクト性の本質を言い表した定理です。

---

---