「数学パズル ボルツァーノ=ワイエルシュトラスの定理 2 (2020/08/11)」
前回の復習:
ボルツァーノ=ワイエルシュトラスの問題:
0.0~1.0の間に、∞個のランダム数値を用意したら、
1. とある区間[α,β]内に∞個の数値が集まってるゾーンが必ず出てくる。
2. そして区間のサイズ、β-αの値は任意の幅まで狭める事ができる。
(狭めた後でも、区間[α,β]の間には∞個の数値が存在する)
3. 究極的にはβ-α=0。つまりα=βまで狭める事によって
無限の点が収束するポイントがある。
何故でしょう?
0.0~1.0の間に、∞個のランダム数値を用意したら、
1. とある区間[α,β]内に∞個の数値が集まってるゾーンが必ず出てくる。
2. そして区間のサイズ、β-αの値は任意の幅まで狭める事ができる。
(狭めた後でも、区間[α,β]の間には∞個の数値が存在する)
3. 究極的にはβ-α=0。つまりα=βまで狭める事によって
無限の点が収束するポイントがある。
何故でしょう?
これは・・・自明ではありません。
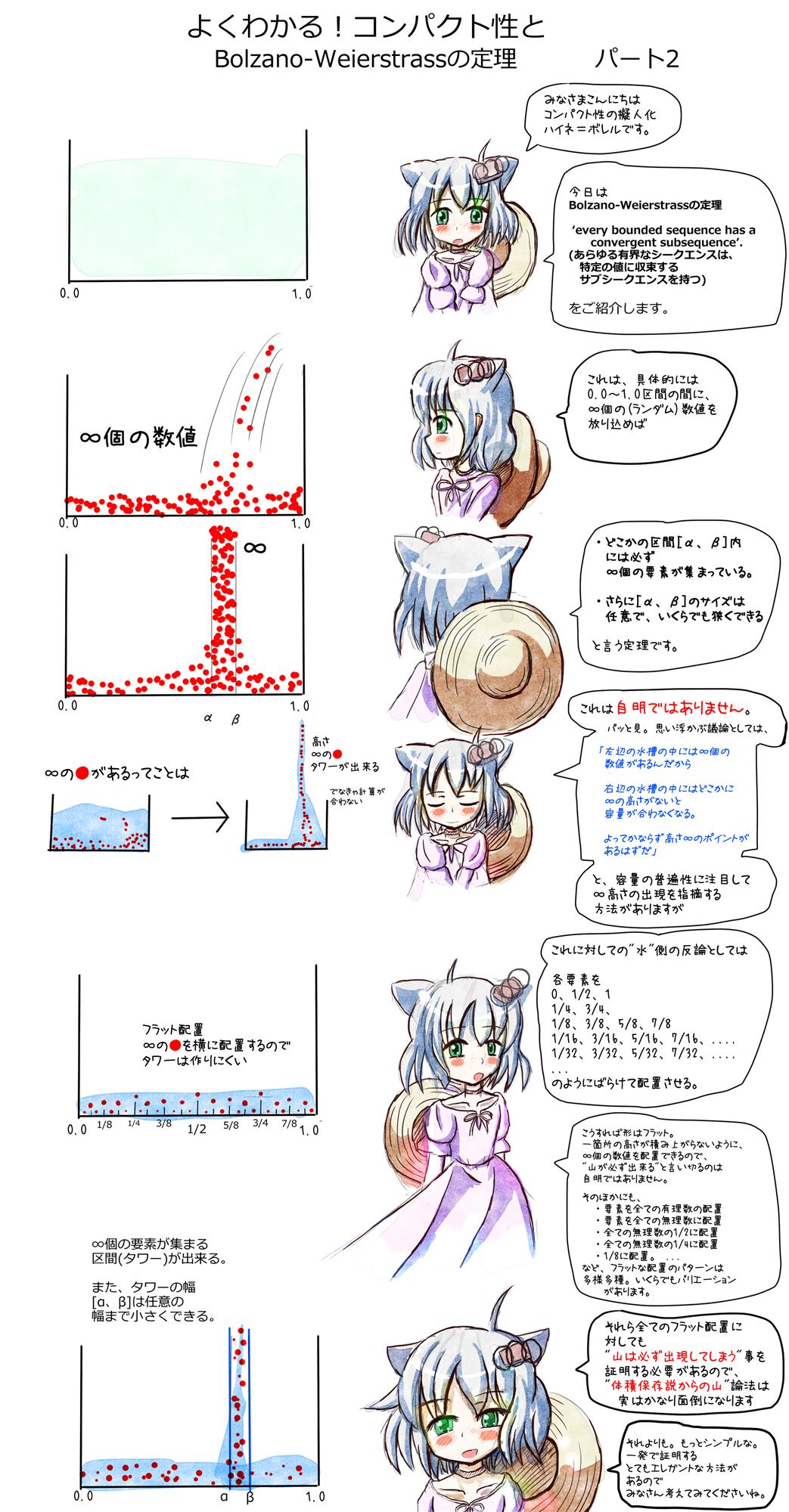
パッと見、思うのは
「∞の要素が水槽内に詰まってる以上 = 容量∞、
どこかで高さが∞にならないと容量∞が処理できないので
必ず山ができるはず。」
と請求する方法ですが。
これはこれで。
水槽側も要素を
0 , 1/2 , 1
1/4, 3/4
1/8 , 3/8 , 5/8 , 7/8
1/16 , 3/16 , 5/16 , 7/16...
1/32 , 3/32 , 5/32 , 7/32...
となるべくフラットに。できるだけ山を作らないよう低く並べる
方法もあるので
「∞の要素があるのだから容量保存の法則で 必ず山が出現する」
との論法は必ずしも自明とも言い切れません。
それがこの問題を難しくしてるんですね。^_^;
ところが、超~~~シンプルなやりかた。
誰でも理解できる、恐ろしく簡単な方法で。
ボルツァーノ=ワイエルシュトラスの問題:
0.0~1.0の間に、∞個のランダム数値を用意したら、
1. とある区間[α,β]内に∞個の数値が集まってるゾーンが必ず出てくる。
2. そして区間のサイズ、β-αの値は任意の幅まで狭める事ができる。
(狭めた後でも、区間[α,β]の間には∞個の数値が存在する)
3. 究極的にはβ-α=0。つまりα=βまで狭める事によって
ただ一点の上に∞個の数値が乗ってる収束ポイントがある。
何故でしょう?
0.0~1.0の間に、∞個のランダム数値を用意したら、
1. とある区間[α,β]内に∞個の数値が集まってるゾーンが必ず出てくる。
2. そして区間のサイズ、β-αの値は任意の幅まで狭める事ができる。
(狭めた後でも、区間[α,β]の間には∞個の数値が存在する)
3. 究極的にはβ-α=0。つまりα=βまで狭める事によって
ただ一点の上に∞個の数値が乗ってる収束ポイントがある。
何故でしょう?
を証明する方法が存在します。
次回にそれをご紹介。
