「数学パズル ボルツァーノ＝ワイエルシュトラスの定理 1 （2020/08/05)」


数学パズルをしましょう。

0.0～1.0 の範囲にある、ランダムな数値をいくつか用意します。

　　例えば円周率の最初の1万桁
3.1415926535897932384626433832795028841971
69399375105820974944592307816406286208998628034825
34211706798214808651...

これを9桁で区切り、1,000,000,000で割ることで
a[0] = 0.141592653
a[1] = 0.589793238
a[2] = 0.462643383
a[10] = 0.342117067
a[100] = 0.59825349
a[1000] = 0.958897069

のようなランダムな数値を約1000個生成する事ができます。


次に、このa[0～1000]を特定の順番で並び替えると
これらの値は0.561814675と言う一点の数値に
収束します。

要素　　　　値　　　　　　0.561814675との距離
a[1006] 0.564056448 0.00224177299999995
a[1109] 0.560010165 0.00180451000000004
a[529] 0.560290228 0.0015244470000001
a[972] 0.563025494 0.00121081899999997
a[819] 0.562710953 0.000896277999999917
a[470] 0.562230538 0.000415862999999961
a[643] 0.562134914 0.0003202390000000
a[909] 0.562009939 0.000195263999999917
a[422] 0.561809377 0.0000005298000000042
a[329] 0.561814675 0.000000000000000000

これは、自明ではありません。


試しに他の適当な値。
例えば最終目的地として0.1、0.5、0.9などを設定し、
目的地への近さとして要素を並び替えると
↓のようなグラフが出現します。


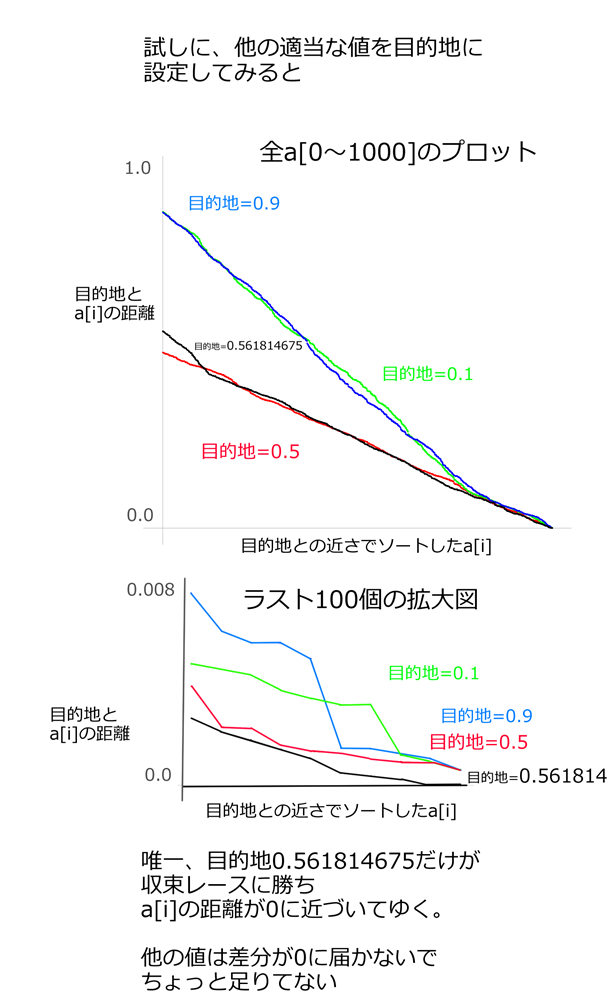
目的地=0.561814675よりも収束度は悪くなります。


もしa[1]、a[500],a[999]みたいな
シークエンス上に既存の値を
目的地に使っても：



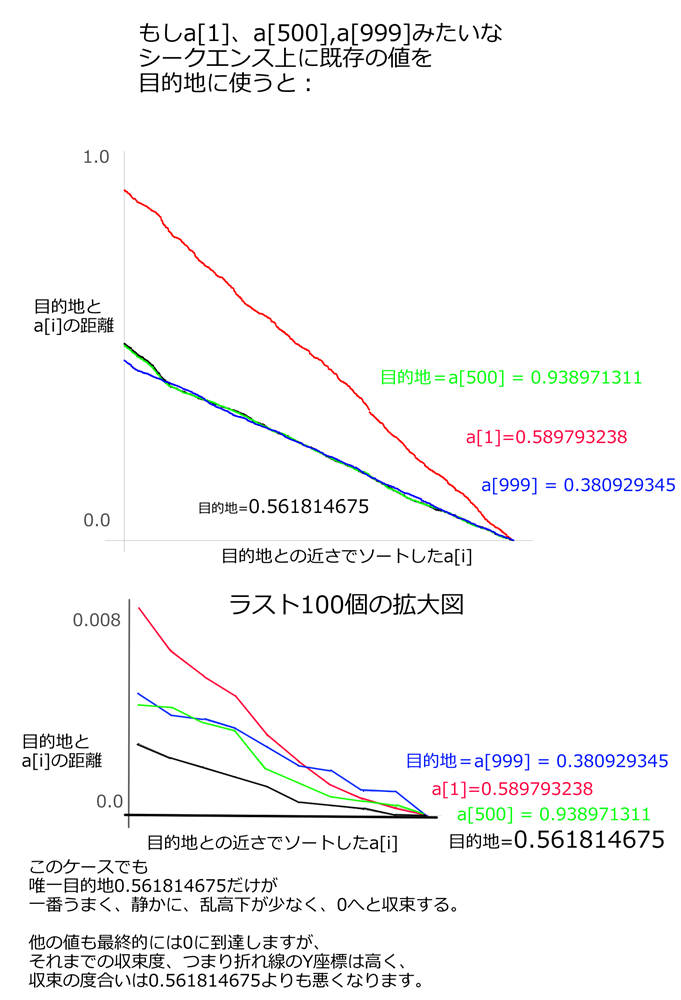
最終的には全てのグラフが0に辿り着きますが、
それまでの過程。
ラインとしての収束度は0.561814675よりも確実に悪くなります。

なぜ0.561814675が収束の最適になるのか。
これは、自明ではありません。




ん・・・・・・まあ。冷静に考えれば、
　　0.0～1.0
の範囲をシラミ潰しに
全ての値を調べれば、

そりゃ
どこかに「収束度がミニマムになる」
地点があるのはわりと明快なので。

力づくで手当たりしだいに調べれば
収束点を見つける事自体はわりと可能なんですが。^_^;


・・・んが
それをちゃんと証明してみろよ！
と言われたらとたんに難しくなる。(；´Д｀)

　これは実は
　　ボルツァーノ＝ワイエルシュトラス
(Bolzano-Weierstrass)の定理
　　　　 ‘every bounded sequence has a
　　convergent subsequence’.
　　(あらゆる有界なシークエンスは、
　特定の値に収束するサブシークエンスを持つ)

と呼ばれる、数学では有名な定理です。


面白い数学パズルなので、
時間に余裕のある方はぜひやってみてください。

ボルツァーノ＝ワイエルシュトラスの問題：
　　0.0～1.0の間に、∞個のランダム数値を用意したら、
　　
　　１．　とある区間[α,β]内に∞個の数値が集まってるゾーンが必ず出てくる。
　　
　　２． そして区間のサイズ、β-αの値は任意の幅まで狭める事ができる。
　　　　(狭めた後でも、区間[α,β]の間には∞個の数値が存在する)
　　
　　３．　究極的にはβ-α=0。つまりα=βまで狭める事によって
　　　　無限の点が収束するポイントがある。
　　
　　何故でしょう？


解けそう～～～で解けない。
でも一生懸命考えたら・・・多分誰でも解ける。
数学的な専門知識は一切必要ありません。

やろうと思えば・・・それこそ小学生でも理解できるような
とてもシンプルでエレガントな証明が存在します。


次回に続く。