1+2+3+・・・・ = -1-12 日記

「TREE3の単位とは（2019/05/05)」

前回の復習：
3↑↑↑3
　　= 3↑↑3↑↑3 　(矢印の数を一本減らして、b-1回繰り返す)
　　= 3↑3↑...(7,625,597,484,986回)...↑3↑7,625,597,484,987
　　= 3↑3↑...(7,625,597,484,986回)...↑γ
　　= 3↑3↑...(7,625,597,484,985回)...↑3↑γ

↑記号はとんでもなくデカい数！！

問題は・・・
「↑記号を使えば、大きい数を作れるのはわかった、わかった。
　だが、そんな大きい数を作っていったい何の意味があるのか？」

→答え：TREE(3)がいるから。^_^A;

Q.TREE(3)とはなんぞや？

A.TREE(3)とは：

おはじき三色。赤/青/緑を使ったTREEゲーム。

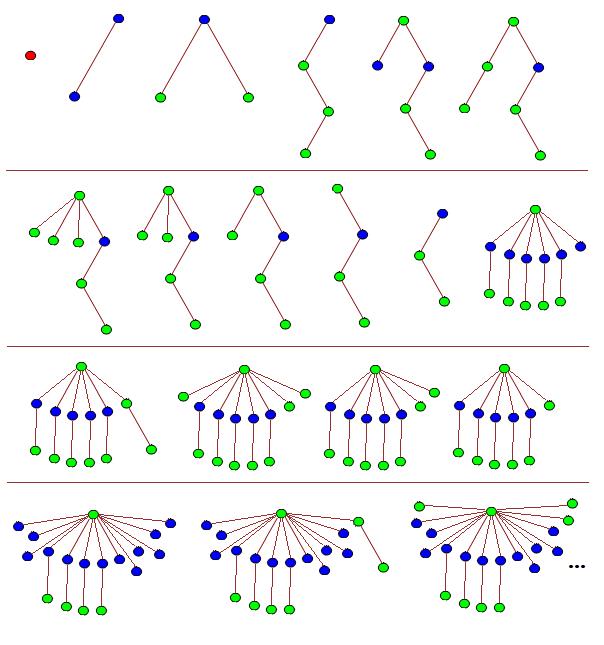https://cp4space.wordpress.com/2012/12/19/fast-growing-2/より

ルールはシンプル：

・n手目に、おはじきn個を使ってツリーを作る
・以前に作ったツリーの相似が含まれていたら、ゲームは終了

わずかこれだけ。

この状況下で
「ゲームを可能な限り長続きさせた場合、おはじきは最大何個置ける？」の答えがTREE(3)です。

TREEゲームは長い時間がかかりますが
いつか必ず、有限時間内に終わることは証明されています。

ただ最長手数が・・・長い。^_^;
あまりにも長過ぎる。

将棋や囲碁の全パターン10³⁶⁰などメじゃない。
前回解説したデカい数 3↑↑↑3も全く相手にならない。

あまりにも巨大すぎて、
　　3↑....(.1兆....)↑↑3
でも全然足りてない。

想像を絶する巨大さすぎて
我々はTREE(3)を記述できる術を持っていないのです。
もっともっともっともっともっともっともっともっと上の巨大数まで
記述できる言語が必要になった。

長い巨大有限数の旅が始まる。

巨大有限数のランクまとめ：

ランク7	3↑↑↑3
ランク7.01	3↑↑↑↑3
ランク7.02	3↑↑↑↑↑3
ランク7.03	3↑↑↑↑↑↑3
ランク7.1	3↑...(矢印 3↑↑↑↑3個)...↑3
ランク7.2	3↑...(矢印ランク7.1個)...↑3
ランク7.3	3↑...(矢印ランク7.2個)...↑3
ランク8.0	ω = 3↑↑(矢印ランク7.64個........)↑3 = グラハム数。

これ以降は
ω+1 = グラハム数
ω+2 = ω+1が「1」に見えるぐらいもっと巨大な数。
ω+3 = ω+2が「1」に見えるぐらいもっともっと巨大な数。
ω+4 = ω+3が「1」に見えるぐらいもっともっともっと巨大な数。

のオーダーでサイズが増えて行き、
ω代入ルール
　　ω＝その場の出てる中で最大にデカい数を代入するシンボル
を採用する。

例1：

ω+ω
　　を見かけたら、
ω+1の時点で「グラハム数」は見えているので
ω → グラハム数
　　を代入して
ω+ω = ω+グラハム数
番目の序列となる。

例2

ω+ω＋ω
　　を見かけたら、
まず最初に
ω → グラハム数
　　を代入して
ω＋ω+ω = ω+ω+グラハム数
　　とする。

この時点では
　　ω+1、ω+2、ω+3....　　　　+1で「グラハム倍々」で肥大してゆく数の配列
　　この配列の、[ω+グラハム数]番目の内容
が最大にデカい数です。

なので次は
ω → [ω+グラハム数番目]の内容
　　を代入して
ω＋ω+ω → ω+ω+グラハム数 = ω + [ω+グラハム数番目]内容 + グラハム数
となる。
これはω+ωよりも超圧倒的に大きい。

ωが一個増えるごとに高いインデックスにアクセスするので
数が爆裂的に肥大化する。

ランク8.5	2ω = ω+ωのショートカット表記
ランク9	ω² = ω・ω = ω+ω+ω+...(ω個)...ωのショートカット表記
ランク10	ω³ = ω²・ω = ω²+ω²+ω²+...(ω個)...ω²のショートカット表記
ランク11	ω^ω = ω×ω×...(ω個)...×ω のショートカット表記
ランク12	ω^{ω^ω} = ω^ω × ω^ω×...(ω個)...×ω^ω のショートカット表記
ランク13	ω^{ω^{ω^ω}}
ランク14	ω^{ω^{ω^ω}}
ランク15	ω^{ω^{...(100000段ぐらい)...}ω}
ランク16	ε=ω^{ω^{...(ω個)...}ω}
ランク16.5	ε₀ =ε ε₁ =ε₀^{ε₀^{...(ω個)...}ε₀} ε₂ =ε₁^{ε₁^{...(ω個)...}ε₁} ε₃ =ε₂^{ε₂^{...(ω個)...}ε₂} ...の ζ=ε_{ε_{...(ω回)..._ε₀}}番目。
ランク16.6	ζ₀ =ζ ζ₁ =ζ₀^{ζ₀^{...(ω個)...}ζ₀} ζ₂ =ζ₁^{ζ₁^{...(ω個)...}ζ₁} ...の ζ_{ζ_{...(ω回)..._ζ₀}}番目。
ランク17	φ関数 = ω→ε→ζ→η...と続くシンボルのω番目。φ_ω
ランク17.1	φ_{φ_ω}
ランク17.2	φ_{φ_{φ_ω}}
ランク17.9	Γ₀=φ_{φ_{φ_{...(ω回)..._ω}}}
ランク18	Γ₁=φ_{φ_{φ_{...(ω回)..._Γ0}}} Γ₂=φ_{φ_{φ_{...(ω回)..._Γ1}}} ... Γ_極大 Γ_(1,0)=φ_{φ_{φ_{...(ω回)..._Γ極大}}} Γ_(1,1)=φ_{φ_{φ_{...(ω回)..._Γ(1,0)}}} ... Γ_{(極大,極大)} Γ_(1,0,0)=φ_{φ_{φ_{...(ω回)..._{Γ(極大,極大)}}}} Γ_(1,0,1)=φ_{φ_{φ_{...(ω回)..._Γ(1,0,0)}}} ... Γ_{(極大,極大,極大)} と続く二次元テーブル。 ※※※　　TREE(3)のサイズがどっかここら辺 ※※※ 最大：Γ_{(極大,極大,極大,....(Γ0個),....,極大)まで}
ランク19	Γ_{(極大,極大,極大,....(ランク18以上の個数),....,極大)}

つまりこのランク18言語が

に対する答えになる。
我々はTREE(3)を記述できる単位/言語を見つけたのです。

「TREE3の単位とは （2019/05/05)」

「TREE3の単位とは（2019/05/05)」