「数学界で近年見つかった、TREE(3)と言うウルトラ巨大な数 8 (2019/01/30)」
数学界で近年見つかった、TREE(3)と言うウルトラ巨大な数についてのお話8 ランク16~17の世界
おさらい。
巨大数ランク表:
| ランク | カテゴリ名 | スケール | 相撲スケール | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 特になし | 10 | 一般人 | ||||||||||||||||
| ... | ... | ... | |||||||||||||||||
| 14 | Triple Exponentiated polynomial omega | ffωωωωω+1 | 小結 | ||||||||||||||||
| 15 | Iterated Cantor normal form | fω...(1,000,000個)...ω+1 | 小結 | ||||||||||||||||
| 16 | Epsilon | fε = fω...(ω個)...ω+1 | 関脇 | ||||||||||||||||
| 17 | Binary phi | fεの次のシンボルζ。その次のシンボルη、その次・・と増えてゆく。| 大関 | 18 | Bachmann's collapsing | fψ(1,0.....0,0) | 横綱 | 19 | Higher computable | fθ(x) | 優勝 | XX | Unreadable | 不明 | 人間じゃない | ZZ | Uncomputable | 計算不可能。 | 生物じゃない | |
前回はランク16:
名称:Epsilon
サイズ:ε0 =
まで作りました。
ε(エプシロン)は未曾有にデカい数なのですが、^^;
一度ε0を作成しちゃったら最後。
ε0 +1 > ε0
ε0 * 2 > ε0 + 1
ε0 2 > ε0 * 2
ε0 ω > ε0 2
εεε...(ω回)...ω > ε0 ω
のようにε0を核にすれば、
ε0より大きい数が作れるようになります。
さらにシリーズ化して・・・
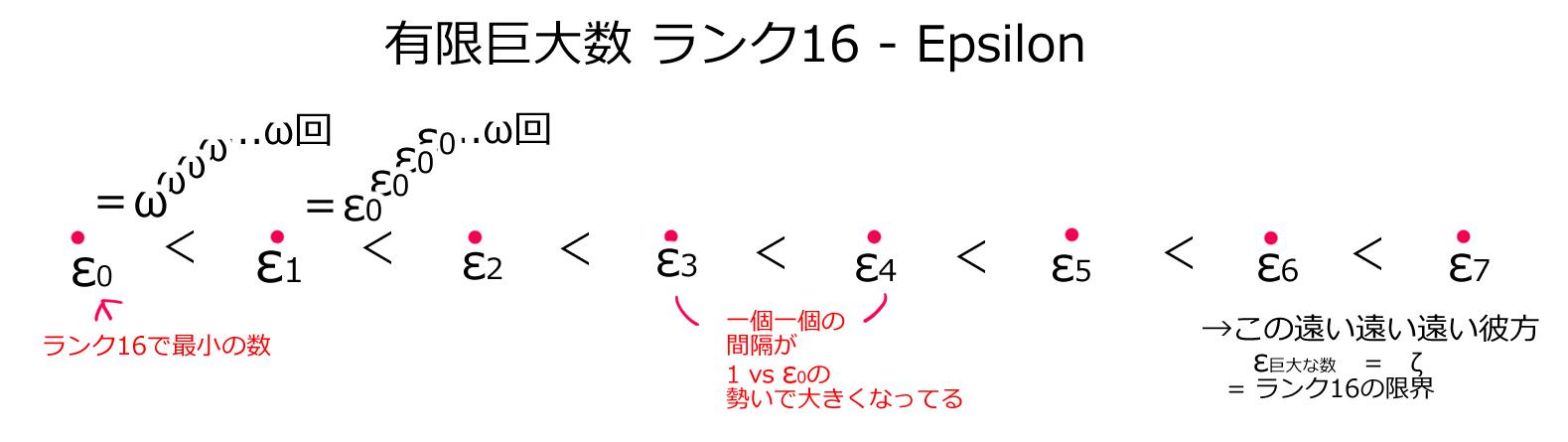
ε1 = ε0ε0ε0...(ω回)...ε0
ε2 = ε1ε1ε1...(ω回)...ε1
ε3 = ε2ε2ε2...(ω回)...ε2
そうすると
ε0、ε1、ε2、....
のε惑星シークエンスができますから、
この中で可能な限り後方のインデックスにアクセスしようとする。
つまり
εα α=巨大な数
が欲しい。
例えば
ε100
ε1,000,000
εグラハム数
εε0
εεε0
εεεε0
...
最大は
εεεε...(ω回)..ε.0 = ζ(ゼータ)
このε&ωで記述できる範囲内のサイズがランク16です。
(何故「ω回」の所。ここだけεではないかと言うと
ω=可算無限(1、2、3、...整数の個数)シンボル。ε=非可算無限 (実数の個数)シンボル。
「ω回」は可算回の演算ですから、使うのはωであって
ε回の演算はできないとの思想から来てます。)
次ランク17:

名称:Binary Phi
サイズ:Φn(a)
ランク16の最後に
ζ(ゼータ) = εεεε...(ω回)..ε.0
が出てきました。
あとはランク16のεと同じ要領で
ζ1 = ζ0ζ0ζ0...(ω回)...ζ0
ζ2 = ζ1ζ1ζ1...(ω回)...ζ1
ζ3 = ζ2ζ2ζ2...(ω回)...ζ2
...
で
ζ0、ζ1、ζ2、ζ3,....
ζ惑星シークエンスを作って、
この中でなるべく高いインデックスにアクセスしようとする。
最大は
ζζζζ...(ω回)..ζ.0 = η(ヌー)
新しいシンボルηが出てくる。
で、これを繰り返してゆけば我々はシークエンス
Φ = {ω、ε、ζ、η,...}
を得る。ここまでくればあとは単純に
Φ0 = ω
Φ1 = ε
Φ2 = ζ
Φ3 = η
...
のように番号をつけてやれば
どれだけ高いω、ε、ζ、η,...でも単純にインデックスでアクセスできるようになる。
で、^^;
次に思うことは
「このΦ関数の中で高いインデックスにアクセスすれば
極大な数が得られそう」デス。
つまり
Φα α=極大なインデックス
最大は
ΦΦΦΦ...(ω回)..Φ.0 = Γ0
これがΦ関数の限界到達値。
Γ(ガンマ)0でありランク17の世界です。
やっとランク17まで来た。
次、いよいよランク18。TREE(3)の領域。
つまり、恐ろしい事に
ランク18:TREE(3)
> ランク17:ΦΦΦΦ...(ω回)..Φ.0
> ランク16:ε、ζ、η、.... こいつらはランク17言語だとわずか「1~3」程度の大きさしか持ってない
これだけ!信じられない。馬鹿げたスケールの肥大化を延々と繰り返して、
まだTREE(3)に届いてないのだ。おいおい・・・^^A;