「数学界で近年見つかった、TREE(3)と言うウルトラ巨大な数 6 （2019/01/20)」



数学界で近年見つかった、TREE(3)と言うウルトラ巨大な数についてのお話 6　グラハム数の一つ上のランクを作る その2



前回までの復習。
巨大数のランク8は
　　fω+1、fω+2、fω+3...fω+1,000...fω+1,000,000...

　　
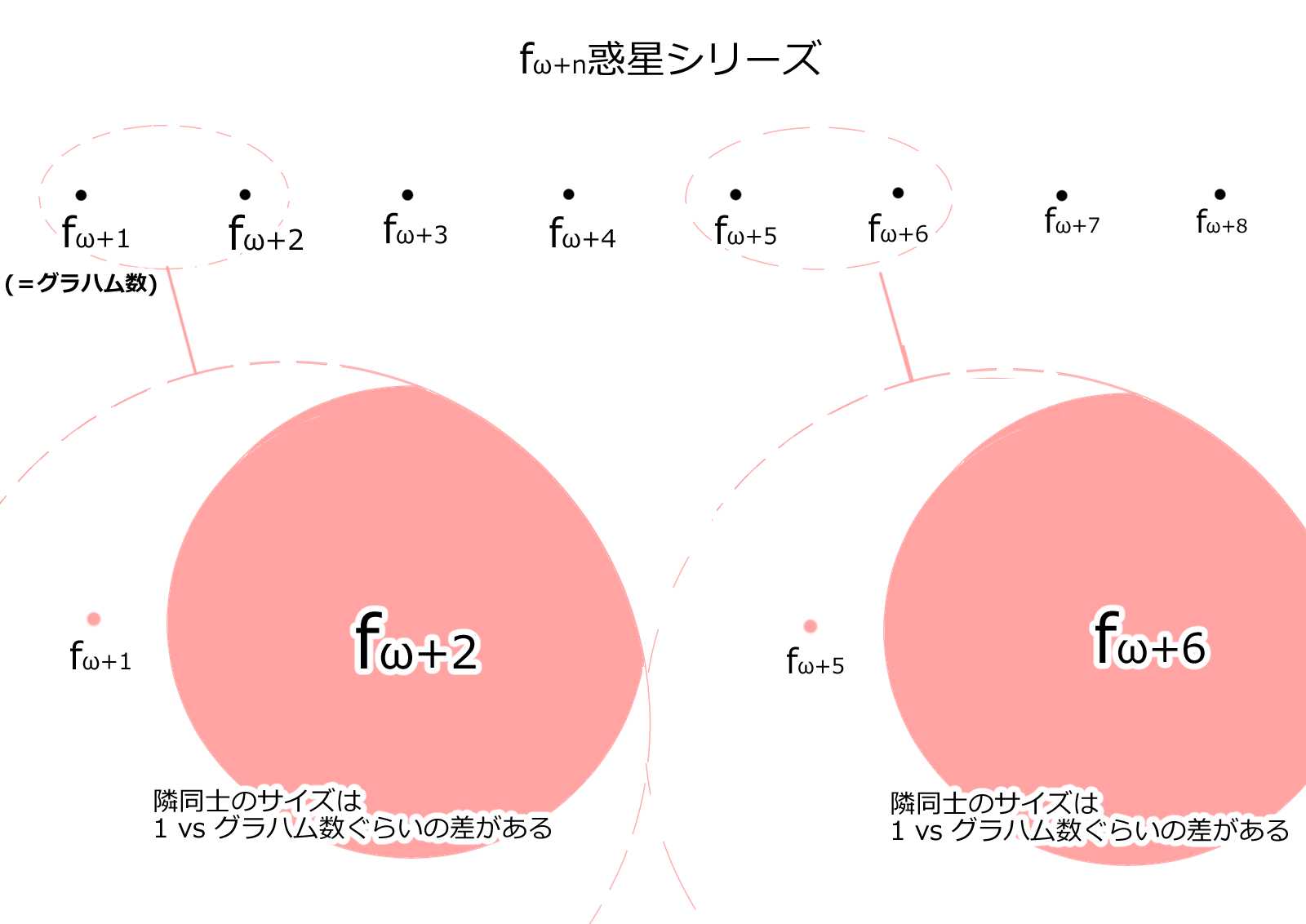
このように惑星みたいに並んでいます。

お隣の惑星同士は
　　1 ～　グラハム数
ぐらいの違いがあります。

ここまでランク8.0～8.4999の世界。



で、ランク8.5～ランク9.0から巨大さは加速する。
つまり、これでもまだ足りないと申されるのだ。^^;

何が起こってるかと言うと
ランク8.5～のサイズは
　　 fω+1億、fω+100兆、fω+100....(0が100億個)...0
のような、
この惑星シリーズの中でもまだまだまだまだ遠い後方にある為に^^;
　　 fω+xxx
のインデックス部分の数値が大きすぎて普通の方法じゃ
記述できなくなってしまうのです。

そこでインデックスを飛ばすワープ航法が必要になります。




話をわかりやすくするために別の例えから出しましょう^^;


例えば基本シークエンスが
　　2 , 4 , 8 , 16 , 32 , 64 , 128 , 256...
と2n (n>=1) で並んでる時。



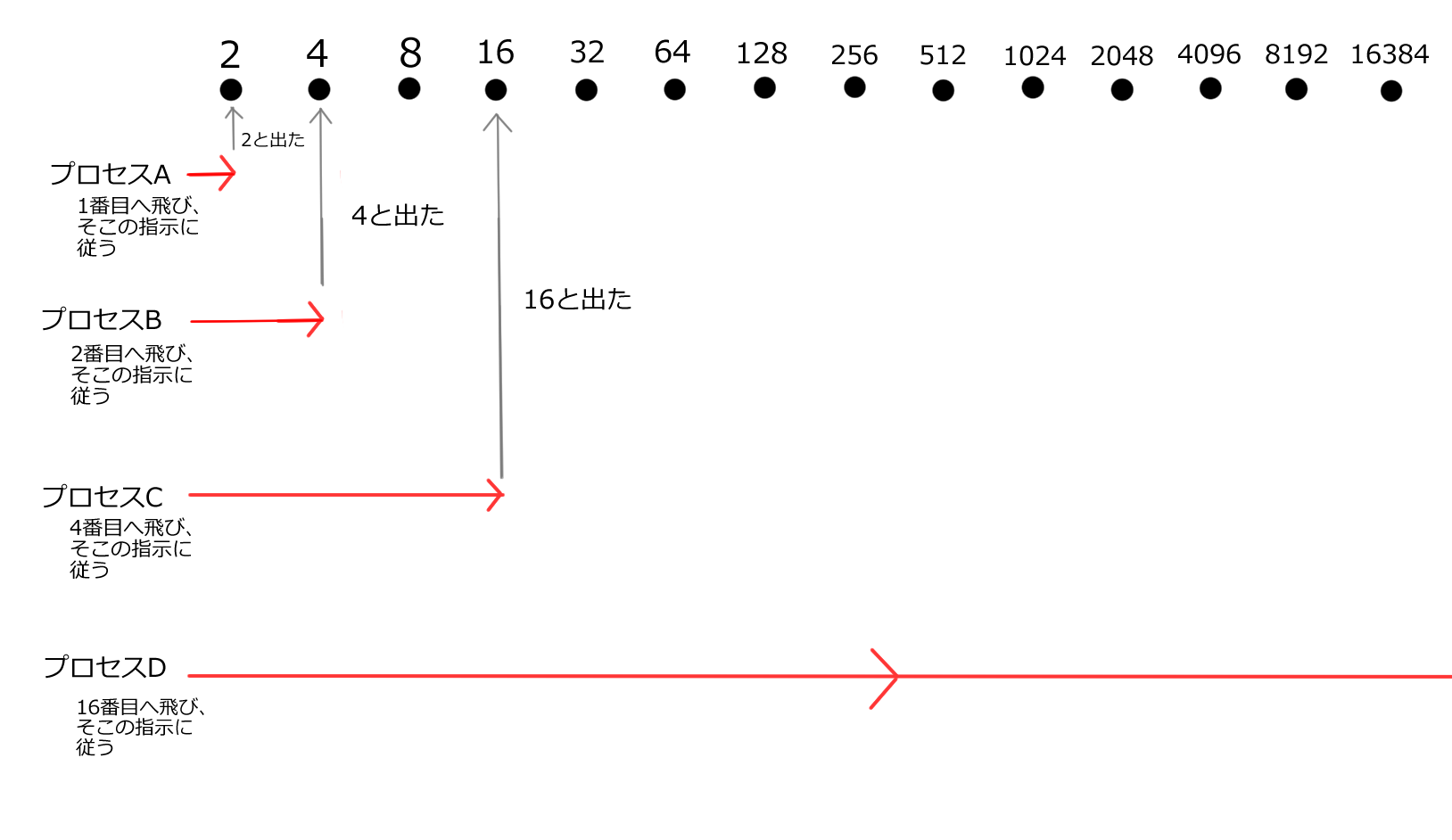
プロセス：
n番目の項目に書かれてる数にジャンプする。

を繰り返した時にどう動くかを見てみましょう。



プロセスA.
1番目の項目に書かれてる数は2。
つまり2番目の項目に移動します。

プロセスB.
2番目の項目に書かれてる数は4。
つまり4番目の項目に移動します。

プロセスC.
4番目の項目に書かれてる数は16。
つまり16番目の項目に移動します。

プロセスD.
16番目の項目に書かれてる数は216+1 = 131072。
つまり131072番目の項目に移動します。

プロセスE.
131072番目の項目に書かれてる数は2131072+1
2131072+1 =1...(0が39455個) ..0

証明：
　　2131072+1 = 10n
　　log10　　2131072+1 = log1010n
　　log10　　2131072+1 = n
　　(131072+1) log102 = n
　　(131072+1) 0.30102999566 = n
　　39456 = n
　　n = 1...(0が39456個) ..0

つまり1...(0が39456個) ..0番目の項目に移動します。

プロセスF.
1...(0が39456個) ..0番目の項目に書かれてる数は21...(0が39455個) ..0 + 1
つまり21...(0が39456個) ..0 + 1番目の項目に移動します。


....

最初の4回。プロセスA～Dぐらいはなんとかなるんですけど。^^;
プロセスEですでに宇宙にある原子の数1080をとっくに
超えちゃって未曾有の数字になります。

そのプロセスを・・・64回続けたあとに到達する場所が
最終目的地。
とてつもなく大きな数字です





これと同じようなことを
　　fω＋n(64)
でやるのが
　　fω＋ω＋1(64)
デス！


試しに
fω＋ω＋1(64)を計算してみましょう。

fω＋ω＋1(64)
= f64ω＋ω(64)
= fω＋ω(fω＋ω(fω＋ω(...64回...)fω＋ω(fω＋ω(64)))))

最後の赤い項目は
fω＋ω(64)
= fω＋64(64)　(FGH式ではω(α)を見かけたらα(α)を代入できるルール。※)
= 惑星シリーズの fω＋64地点
= 話を簡単にするためfω＋64 →　fω＋1(=グラハム数)で近似する。

つまり
fω＋ω(64)　≒ グラハム数



※なぜFGH式で
　　　fω(α) = fα(α)
「fωの中にωを見かけたらω=αで代入できる」
のルールが成立するかついては特に意味はありません。^^;

ただ単に「ωを見かけた時はαを代入できる」。
こういうルールにすると数を爆発的に増やす事ができる。

つまり巨大数の構築/記述/ランク付けなどに
色々と都合が良くなるから
このルールが制定されてるにすぎないんであって。

なぜそうなるのか。意味は考えないようにします。



式に戻ると
fω＋ω＋1(64)
= fω＋ω(fω＋ω(fω＋ω(...64回...)fω＋ω(fω＋ω(64)))))
≒ fω＋ω(fω＋ω(fω＋ω(...63回...)fω＋ω(グラハム数))))

最後の青い項目は
fω＋ω(グラハム数)
= fω＋グラハム数(グラハム数)　(FGH式ではωを見かけたら(α)を代入できるルール)
= 惑星シリーズの fω＋グラハム数地点

つまりこの時点で
　　fω+1、fω+2、fω+3...fω+1,000...fω+1,000,000...
　　
惑星シリーズにおける
　　fω＋グラハム数
番目の要素にワープしたのです。


っておいおい。
気軽にワープしちゃいましたが、
思い返してみると、
　　fω+1 →　fω+2
の間。
たった＋1でさえ[1 vs グラハム数]ぐらい肥大化してるんですゾ。

なのにそれを何億個、何兆個、何グラハム個も平気で飛び越えるって
その先のサイズはどうなってんだ。^^;



また式に戻ると
fω＋ω＋1(64)
= fω＋ω(fω＋ω(fω＋ω(...63回...)fω＋ω(グラハム数))))
= fω＋ω(fω＋ω(fω＋ω(...62回...)fω＋ω(fω+グラハム数))))

最後の緑の項目は
fω＋ω(fω+グラハム数)
= fω＋ fω + グラハム数(fω + グラハム数)　(FGH式では「ωを見かけたら(α)を代入できるルール)

つまり
　　fω+1、fω+2、fω+3...fω+1,000...fω+1,000,000...
　　
惑星シリーズにおける
　　fω＋ fω + グラハム数(fω + グラハム数)
番目の要素にワープしたわけです。

はいはいはいーい。
もうすでに「グラハム個のワープ」が遠い彼方。
そんなんお話にならない速度でまた肥大化しました。



さらにそのワープを合計64回繰り返す・・・

fω＋ω＋1(64)
= fω＋ω(fω＋ω(fω＋ω(...63回...)fω＋ω(グラハム数))))
= fω＋ω(fω＋ω(fω＋ω(...62回...)fω＋ω(fω+グラハム数))))
= fω＋ω(fω＋ω(fω＋ω(...61回...)...
...
= fω＋ω(fω＋ω(fω＋ω(...)))
= fω＋ω(fω＋ω(...))
= fω＋ω(α)
= fω＋α (α)

でカッコの数が減ってって、
最終的にはシングル項目のfω＋α (α)に。

つまり惑星シリーズ
　　fω+1、fω+2、fω+3...fω+1,000...fω+1,000,000...
の途方もなく巨大なインデックスのどこか、

fω＋ω＋1(64)
＝ fω＋α

にたどり着いた。

これがfω2+1
　　fω＋ω＋1(64) = fω2+1(64)
の世界だ。^^;



fω＋ω＋ω＋1(64) = fω3+1(64)
は二重ワープ。

fω＋ω＋1(64)
　= fω＋ω(fω＋ω(fω＋ω(...64回...)fω＋ω(fω＋ω(64)))))

fω＋ω＋ω＋1(64)
= fω＋ω＋ω(fω＋ω＋ω(fω＋ω＋ω(...64回...)fω＋ω＋ω(fω＋ω＋ω(64)))))


fω2+1に比べるとさらに長い時間たらい回しにされ、
ω＋ω＋ωを消化しきるまで
関数を抜ける事ができません。


fω＋ω＋ω＋ω＋1(64) = fω4+1(64)
は三重ワープ。

...

これを64回。63重ワープするようになると
　　fω＋ω＋ω＋ω...(64回)... ω + 1(64)
　　= fω64+1(64)
　　= fω・ω+1(64)　(FGH式では「ωを見かけたら(α)を代入できるルールの逆適用)
　　= fω2+1(64)



・・・・・・・・・・・ようやく辿り着いた。
この
　　fω2+1(64) = quadratic omega = ランク9
こそが、我々が待ち望んでいたランク9の数です。

あー、デカいね。これは。( ﾟдﾟ)ﾎﾟｶｰﾝ



いや。(ヾﾉ･∀･`)ﾑﾘﾑﾘ

ここまで来るとあまりにも大きすぎて、人間の理解を超えてる。
ランク8ならまだ「グラハム数　＝　とてつもなく巨大」ってわかるんですけど、
ランク9まで来るとわけわからん。^^;

理屈で考えれば
筋が通ってるのはわかりますし理論は展開できます。

が、直感的な感覚でこのサイズを把握するのはちょっと・・・無理じゃないでしょうか。(-_-)

少なくとも私は無理です。(きっぱり)


次回、ランク数と実例の必要性