「数学界で近年見つかった、TREE(3)と言うウルトラ巨大な数 5 （2019/01/12)」

数学界で近年見つかった、TREE(3)と言うウルトラ巨大な数についてのお話 5　グラハム数の一つ上のランクを作る その1

(2019/01/13に修正、加筆。
　ω+ω式の理解を私が完全に間違っていました。orz
　文献をもう一回読んで、理解した・・・と思う段階で全面的に書き直しました。すいません。m(-_-;)m)


前回の復習：グラハム数の大きさはランク8でした。


FGH(Fast-growing hierachy)という、関数の大きさを計る言語で
ランク8は約 f_ω+1(64)の大きさを持っています。
そしてランク9は約 f_ω²+1(64)です。



グラハム数ランク8(サイズ f_ω+1(64))を、
ランク9 (f_ω²+1(64))へと昇格させるには
どれだけ頑張る必要があるかをこれから解説。^^;


たぶんね、想像するより遥かに圧倒的に超膨大な大きさになる。

---

復習：



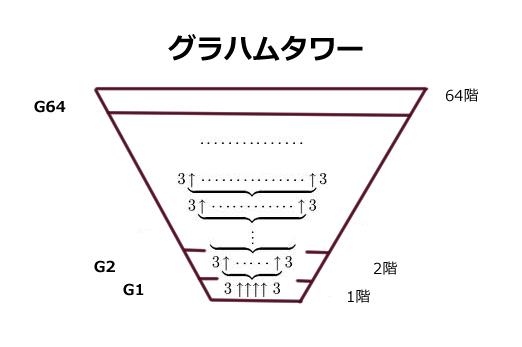
でした。

この時のサイズがFGHスケールでf_ω+1(64)。

まずはこれを1アップ。f_ω+2(64)へ引き上げるのが
最初の目標。

---

さて、このグラハムタワー。

G64の値はとんでもなく膨大なのですが。
それにしたって「64」階建てというのはここだけ数値が低すぎる。
ここをもっと大きな数字にすれば
サイズを上げれそうです。

何階建てにする？

そうですね。G64階層にはG64人の住人がいますから、
彼らに手伝ってもらい、1人が1フロアを担当すれば
64階　→　G64階建てまで高さを増やせそうな気がする。

---

実際にやってみた^^;　↓


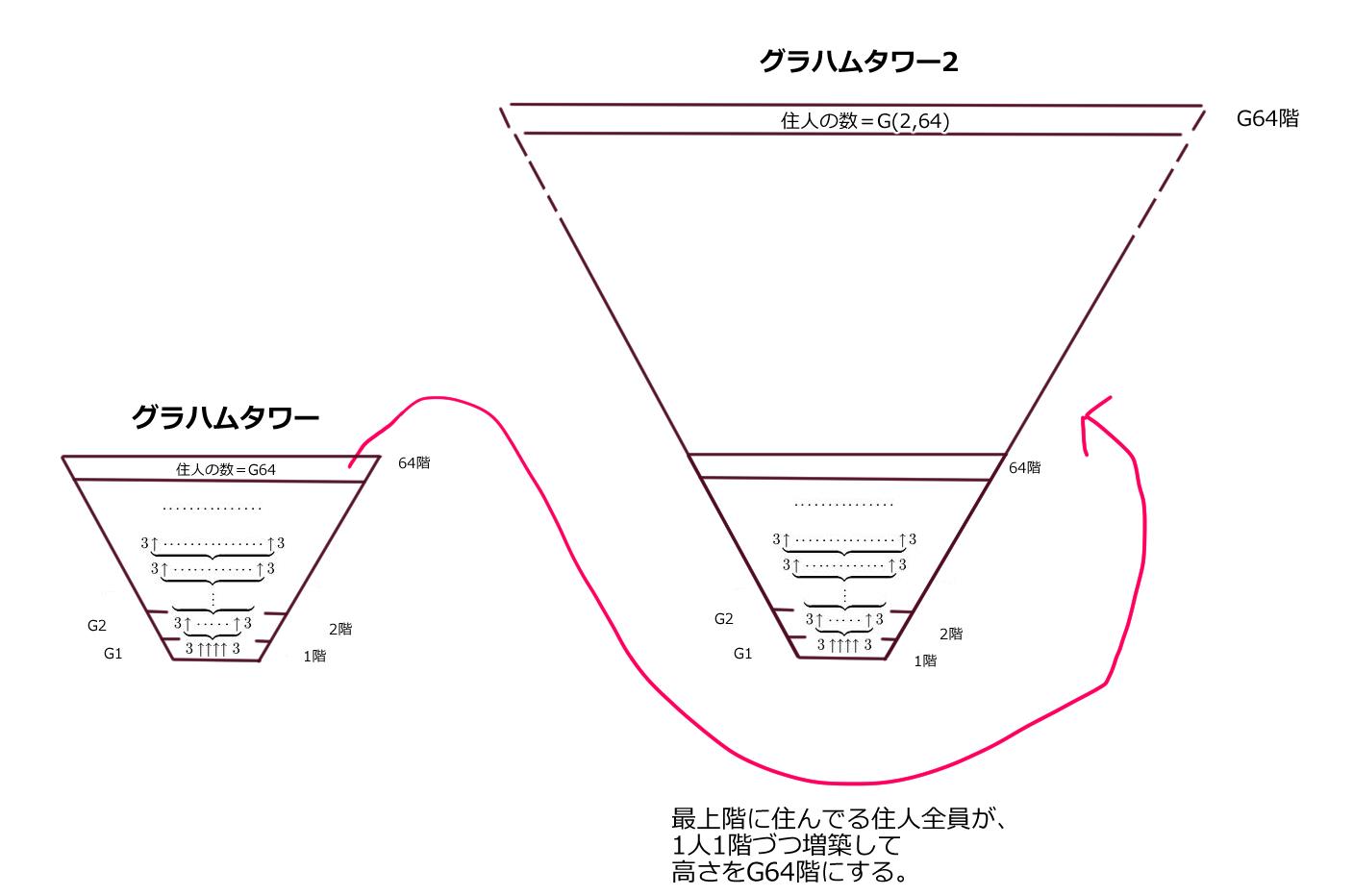
うーん、64階建ての時点でギネスブックに載るほど異常な大きさだったのですが・・・
これでタワーはG64階になりました。

これがf_ω+2(64)？
・・・いや。これはf_ω+1(f_ω+1((64))と呼ばれる数。違う値。

まだたった1/64しか進んでないんですわ。(汗)

---

次に、
グラハムタワー2の最上階には膨大な数の住民が住んでいますが、
今度は彼らに手伝って貰い、1人が1フロアを担当すれば
G64階建て → [G64階に住む住人の数]階まで高さを増やせます。

---

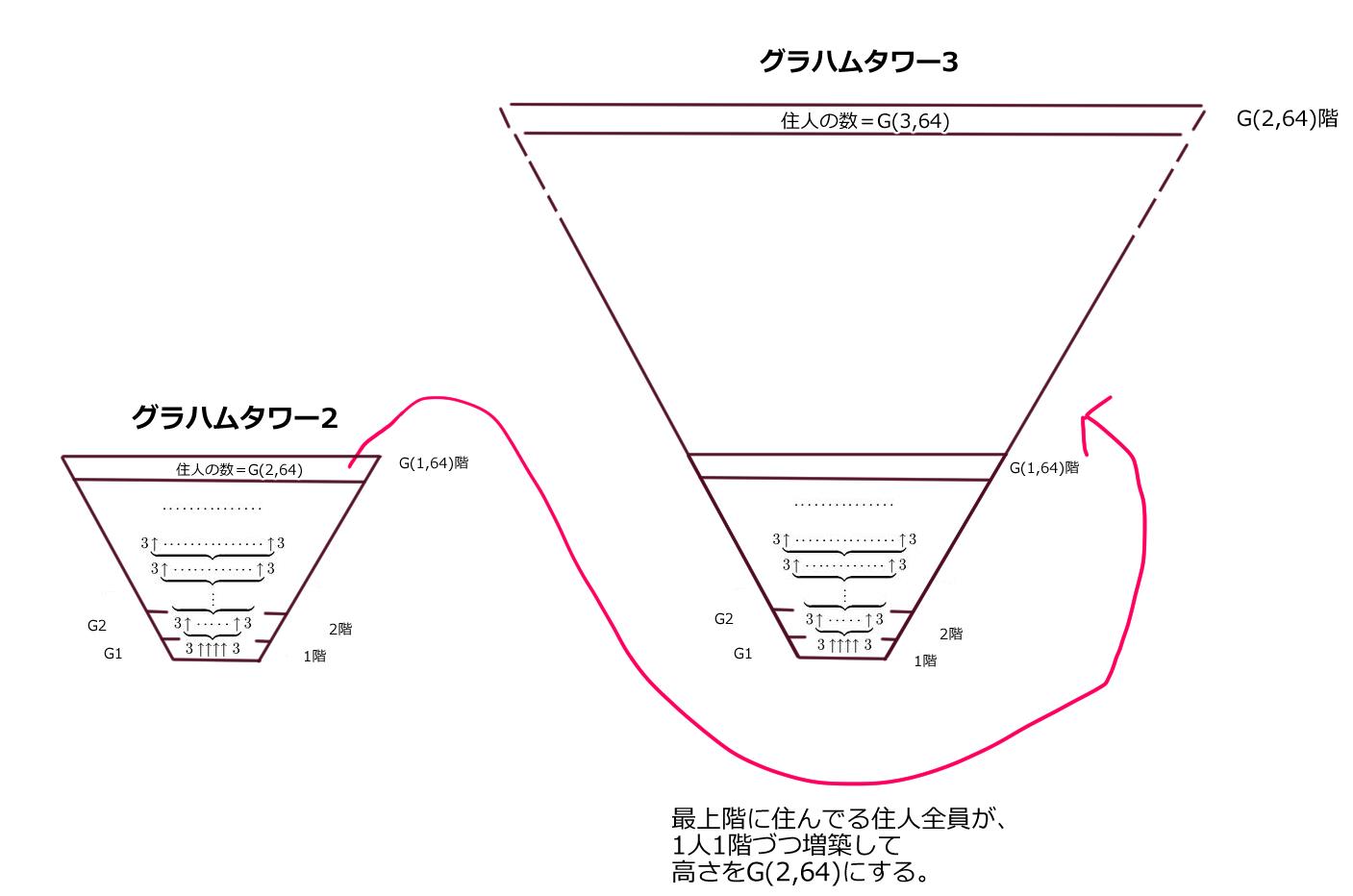
次に、
グラハムタワー3の最上階には膨大な数の住民が住んでいますが、
彼らに手伝って貰い、1人が1フロアを担当すれば
G(2,64)階建て → [G(3,64)階に住む住人の数]階まで高さを増やせます。

---

....この
　　「今建ってる最大のタワーの最上階に住む住人に手伝ってもらい、人数の数だけ階を増やす」
拡張を64回繰り返した後の図がこちら。



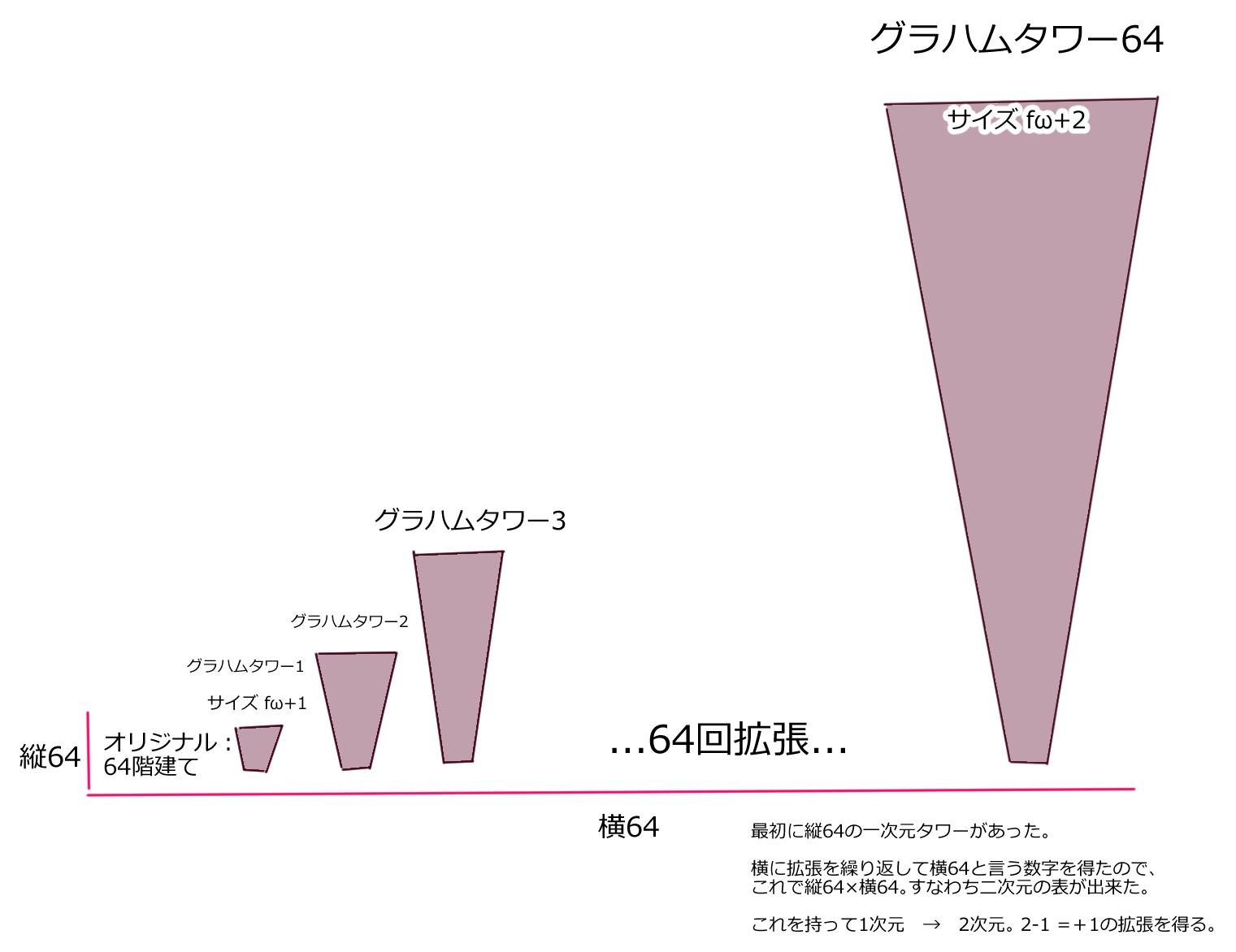
元が64階のタワー。すなわち縦64マスの一次元線だったものが、
横にも64マス広がり、
64×64。縦横に64の数字が揃う事で二次元表になりました。

すなわちこれでようやく
1次元グラハムタワー　→ 2次元グラハム表
への拡張が完了したことになります。

・・・・で。
この時のサイズの増加は・・・
　　1次元 → 2次元
で+1の増分。

なのでFGHスケールは
　　f_ω+1(64) = G₆₄ = グラハムタワー1の最上階に住む住人の数
　　f_ω+2(64) = G_{G...(64回)...G64} = グラハムタワー64の最上階に住む住人の数
で、ようやくω+2を実現させたのであります。

FGHスケールをたった+1するだけで
これだけの馬鹿デカい拡張工事が必要なのだ。(^^;

---

じゃあ次の
f_ω+3(64)
を作るプロセスはさっきの
　2次元表　→ 3次元立方体
にする・・・



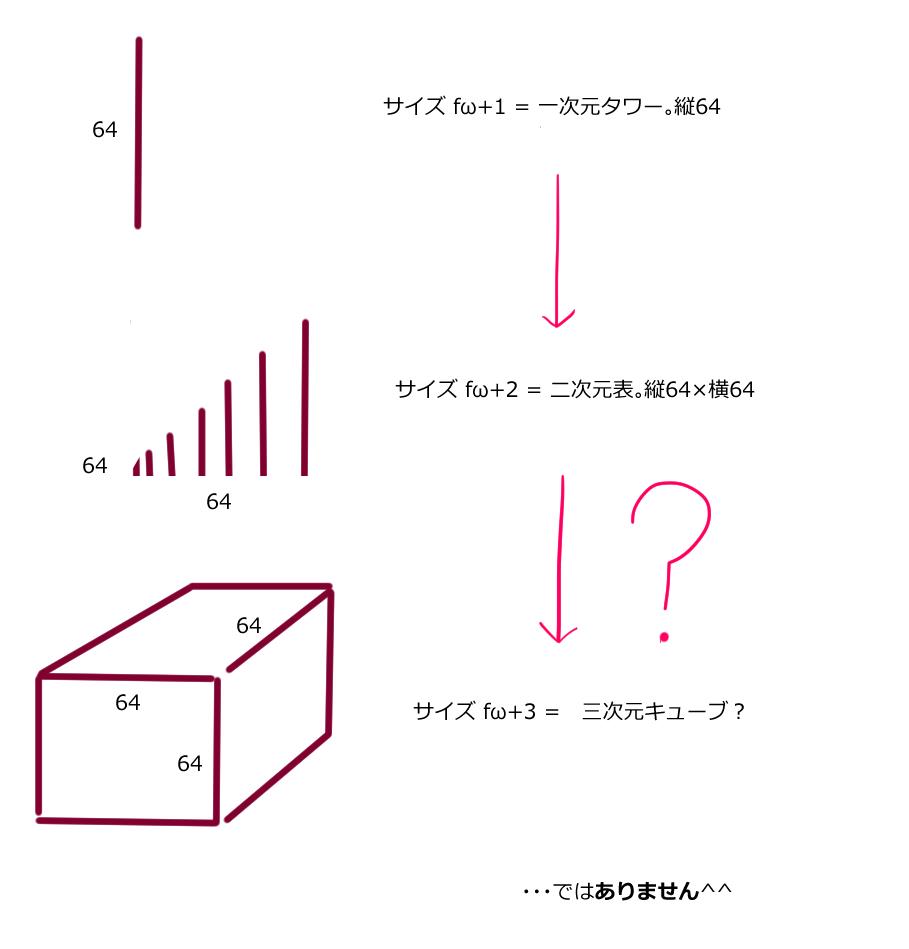
ではありません。^^;

---

最初の
　　f_ω+1(64)　→　f_ω+2(64)
にする過程で
何をしたかって思い出すと・・・



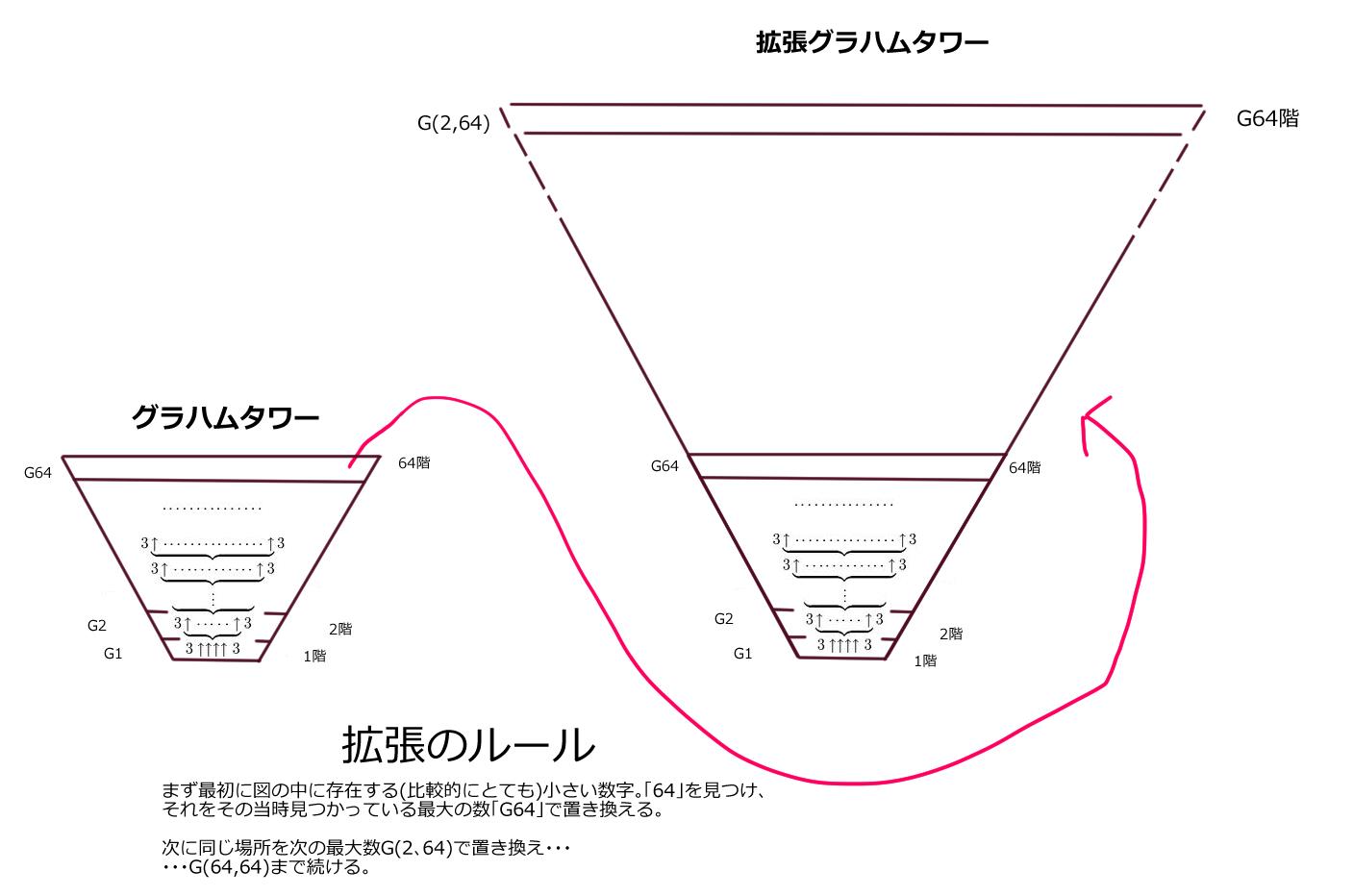
最初に「64」階建てが目に入って、
「64」がさすがに低すぎると思ったのか
それを「G64」階建てにする所からスタートしました。

---

f_ω+2(64) → f_ω+3(64)
も同じ。



「64」回の横拡張はちょっと少ない。
もうちょっと増やしたいな。
どれだけ？

このグラハム表の中に出てくる一番デカい数字は
「グラハムタワー64の最上階に住む住人の数 = G(64,64)」です。

せっかくそれだけのマンパワーがあるんですから
彼らに手伝ってもらって、
人数の数だけ横に拡張します。



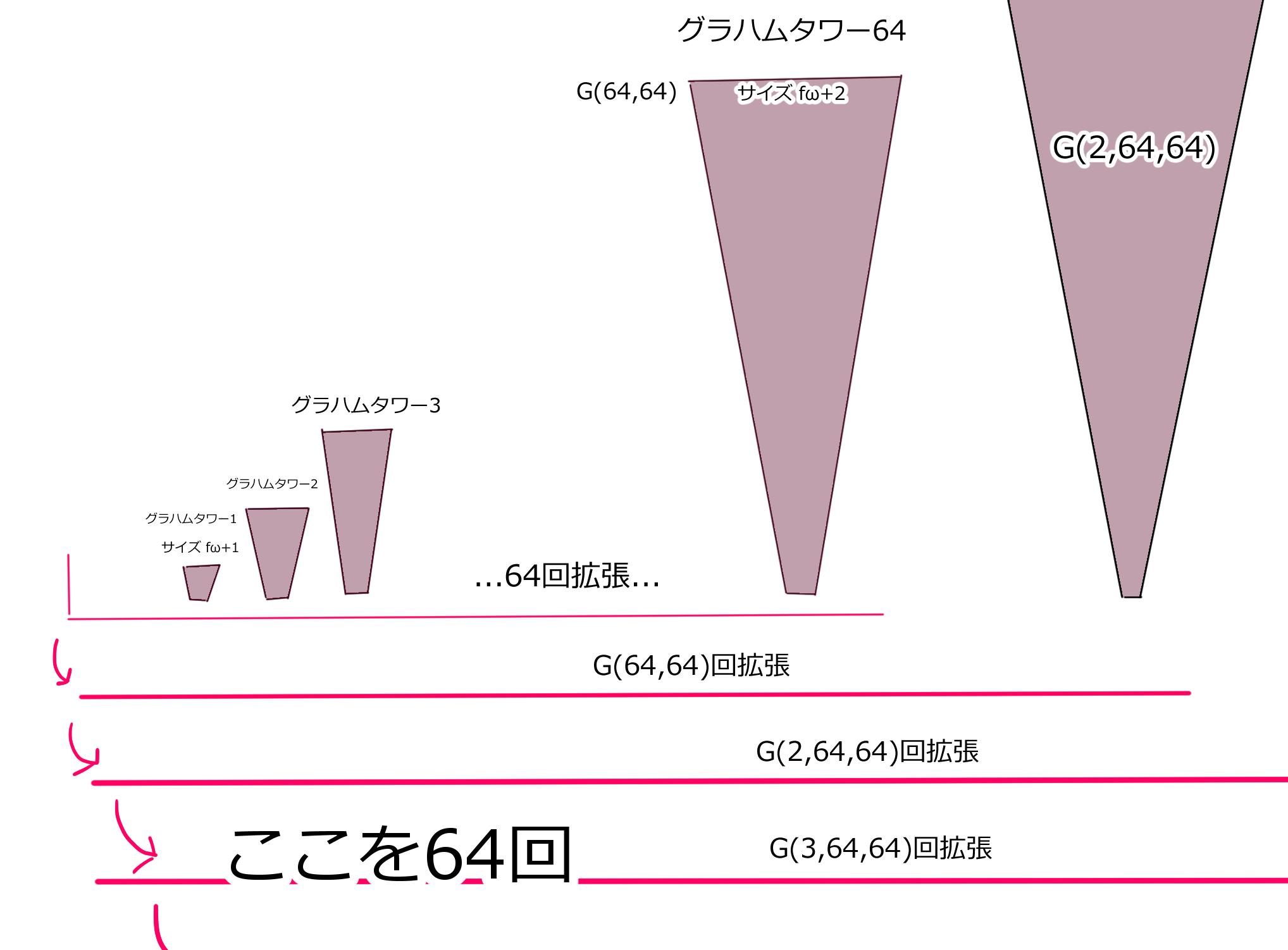
横に拡張したら新しいタワーが横にデデンとG(64,64)棟だけ建ちます。

次はそれらの最後のタワーの、最上階人数の分だけ横に拡張して、
・・・

これを64回繰り返すとさきほどの
　　f_ω+1(64) → f_ω+2(64)
へ増加したのと同じ原理で
　　f_ω+2(64) → f_ω+3(64)
が得られます。

これがf_ω+3(64)。

---

次 f_ω+4(64)。

さきほどの図


には「ここを64回」というなんだかとても小さな数が見えた。
そこを「G(3,64,64)回」に置き換えます。

次に新しく建ったタワー群の最上階住民でG(4,64,64)回に拡張して、
次に新しく建ったタワー群の最上階住民でG(5,64,64)回に拡張して、
...


これを64回繰り返すと。
f_ω+4(64)が得られます。

---

この

を1メソッドとして繰り返してゆけば

　　　f_ω+1(64) → f_ω+2(64) →　f_ω+3(64) ...
　　
とサイズがどんどん上がってゆき...やがては
　　　f_ω+1000(64) ... f_ω+1000000(64) ... f_{ω+10000000000}(64) ,
とどこまでも増やす事ができます。

---

が、まだ先がある。^^;
何故ならこのシークエンスはf_ω+n(64)と、＋記号を使った伸びだからである。

一般には＋記号コンビネーションよりも×記号コンビネーションの方が
速く伸びます。

例：
　　

えー、つまり「＋記号なんか使ってるの？　それは遅いよ」と主張する勢力がいて。^^;

　　f_{ω + n}(64)
で＋記号を使ってシークエンスを伸ばすよりも
　　f_{ω × 2}(64)
と、×記号を使ったシークエンスの伸ばしをさせる方が
＋バージョンよりも圧倒的に速く数値が伸びる事が予想されます。


なので、次は
f_{ω × 2}(64)
を定義すること、その意味を考える事が目標になります。

---

まとめ

＋ステージ：
↑ここまで解説した。

×ステージ：

---

やべーわ。このインフレの絶望さ。orz

あのグラハム数。64階建ての時点で信じられない大きさだったのに、
それがいきなりG64回建てに超増築。

それからもやってる事が一段階、一段階。全ての過程で
一つ前の状態を軽くふっとばす圧倒的なスケールアップ。
それが前座となりさらにXXX回も反復適用され、
気が遠くなるほど膨張しながらサイズが増え続ける。

ここまでやって、ランク8.0　→　8.5ぐらいですねー。

ランク8.5 → ランク9.0の間は更にインフレが進んで
　　f_{ω+1000.......(100兆個)....000000}(64)
じゃ全然足りない。
　　f_{ω+1000.......(グラハム数個)....000000}(64)
でも全然追いつかない。
猛烈なスピードで加速しだす。


んで、TREE(3)はランク18(；▽； )

うっそ～～～ん！！！！

んなバカな。そのランク9.0がまるでお話にならない。
あれだけ馬鹿みたいにインフレさせて、
まだ全っ然足りてない。

こんなもんじゃまだまだまだまだ足りない。マジで予想を遥かに超える巨大なサイズなのです。


少しはわかってくれたかな。(^_^;
TREE(3)のサイズのヤバさ。
ホント。なんでここまで異常すぎる。巨大な物体が、存在できるんでしょうか・・orz

次回。f_{ω × 2}(64)の定義と計算方法を説明します。

---