1+2+3+・・・・ = -1/12 日記

「マリオカート8 スタジアム1分39秒955 （2015/01/07)」

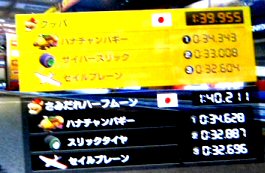LAP内訳
出たー。
マリオカートスタジアム 1分39秒955(WR+4秒503)
念願の1分40秒切り達成。

あー、わかってきたわかってきた。

「スーパーミニターボ　→　サンダードリフト　→　ねじりドリフト　→　ねじれの最後の一回（可能な限り遅らせた着地ドリフト）でそのまま次のカーブに入る」

最後のねじれからのドリフト体勢移行が速い。

　・着地ドリフトによるインをつける効果（着地じゃないと必ず外に膨らむ）
　・着地ドリフトによる早溜め効果
　・ねじり続行によるミニミニターボ

とか副産物が色々ついてきてナイスなんですよ。
最強過ぎて「ねじれドリフトをした後のコーナーは、この一手しかない」って状況になる。

ま、速いって言っても1コーナーにつき0.1秒程度の差しか出ないような微差ですが・・・´･ω･`)
3LAP実行すれば確実に0.3秒は速くなる。2コーナーなら0.6秒。これはTAで大きい。

しっかし。
これでまだランカークラス、
WRと1秒以内の差で争える人たちとの間には
4秒の差があるって。
どーーーやってあと4秒も伸びるんですか。（汗汗汗）

まだ下りのスローダウンサンダー、同スローダウンサンダーからの最高速JAなしジャンプ、ねじりの回数がWRに比べて
だいぶ少ないとかやってない事はあるので
あと1秒ぐらいはなんとかなるような気がしますが・・・・
これ以上タイム伸ばすには「しなければならない事」「しちゃいけない事」リストが果てしなくて増えてきて
キっツいっす。；ﾟдﾟ)
ただでさえねじりドリフトが入ってレバー入力頻度が以前の倍ぐらい増えたのに・・・この先はもっと大変になる。

WR＋5秒切り出せたので自分なりには満足。これ以上は保留とします。

他のコースもTAやってるのですが全コースの平均はWR+8.7秒。
現在はミュージックパークにアタック中で、WR＋9秒を切るのに四苦八苦してる状況。
私の実力なんてそんなものですよ。（´д｀;

----------

更新遅れてすいません。
今から今年の数学コラム書き始めます。

お題は「選択公理」について。

これが相当なくせ者。
一見明確で、直感的には明らかに『正しい』と思うのですが
パラドキシカルな結果を数多く招き、
その危うさに
数学界全体に
　「・・・・もしかしたら選択公理は矛盾を含むかも（しれない）。危ないからしばらく選択公理の使用は禁止」と
お触れが出たほどの物騒な代物。

（その後の研究によって選択公理に矛盾はない、使ってOKとの判定が出ましたが。
　実際それ以前は真偽が不明で本当に危ない状態でした）

それについて解説します。

「数学コラム数学界に大論争を呼んだ選択公理（2015/01/12)」

数学に「選択公理」と言うのがあります。

これはZFC公理体系、すなわち現代数学を支える
大黒柱の一本とされるほどの超超超重要な公理です。

しかしながら

　「・・・・もしかしたら選択公理は矛盾を含むかも（しれない）。危ないからしばらく選択公理の使用は禁止」

との疑惑が勃発し、

　「選択公理は採用するべきだ/しないべきだ」と

過去の数学界を真っ二つにするほどの大論争を呼びました。

ちなみにZFCのCはAxiom-of-Choice。すなわち選択公理。
Cだけ最後にちょこーっと付け加えられてるのは
この争いに争って、
「ZFが基本だから。使いたい人だけオプションで選択公理を使えばいいよ」って事になったからです。^^;

数学の大前提ZFC公理体系の名前に
傷跡を残したぐらい、
大変ないきさつのあった公理です。

それを解説します。
---------------------------

さて、「選択公理」とは「与えられた集合の族に対し、各集合から適当な要素一つを選択し、新しい集合を構成する事」です。

もっと正確に言えば、「選択関数の存在」、
および「選択関数からは矛盾が引き起こされない事を数学的に保証する」
事を言います。

選択公理の例:
　入力S＝{ {A,B,C,D,E} , {い,ろ,は} , {α,γ,ζ,δ} }
　　　↓
　出力D＝{A,ろ,δ}

このように入力集合Sの中から要素を1つ選び、それらを集めて出力集合Dを作ります。

さて。
選択公理自体は「自明」なんですよねー

いや。
どうもこうも。

　入力S＝{ {A,B,C,D,E} , {い,ろ,は} , {α,γ,ζ,δ} }
　　　↓
　出力D＝{A,ろ,δ}

あまりにもシンプルすぎて、いったいこのプロセスのどこに文句のつけようがあるのかってぐらい自明。

強いて言えば結果に一貫性がない、どのメンバーが選ばれるのかわからないってのがフワフワとしてる。
数学的には関数の定義（関数の定義：入力→出力へのマッピング。結果は一意的。）を満たしてないのは不安に感じますが。

しかし選択公理は
　『どのような選び方をしたって、その後には結果的に全く同じ現象が発生する』
ような状況にのみ使われるので
選ばれ方はどうでもいいんです。

どうしても気になるなら「選択には最小のメンバーを選ぶ」とでも勝手に決めればいいし・・・
ま、そこは議論の本質ではないです。

選択公理のヤバい所は・・・縦↓じゃなくて横→の方なんですね。^^;

例えば：

　入力S＝{ {1,2} , {3,4} , {5,6} , {7,8}・・・・・・　（→　横方向には無限の広さがある）
のように実数を2つの数字の組に分けた集合を考えます。

ここに選択公理を適用すると
　入力S＝{ {1,2} , {3,4} , {5,6} , {7,8}・・・・・・
　　↓
　出力D＝{2,4,5,8・・・
のような、Sを入力に取りDを出力に取る集合が出てきます。

・・・これが、実はヤバい。（汗）

と言うのも
「選択」と言うのは1つの動作であるわけです。
入力Sは無限の要素を持っていますから、
それに入力S→出力Dを作るには
「選択」を無限回行わなければいけない。

それは果たして可能であるのか？

しかし普通に考えたら

『いや、その論点は実にくだらない。選択など人間の主観にすぎない。数学的な選択にかかる時間は0なので、無限回の選択を行っても
　かかる時間は0×∞＝0。
　無限回数の選択を瞬時に行い入力S→出力Dを作る事には全く問題がない』

との反論がすぐさま飛んでくるのは予測できます

・・・いや、それはごもっとも。私も全面的に同意し、その上で申しあげます。m(_ _)m

なぜ私が選択公理に対してそんなケチ（選択は有限の動作。無限回の選択を許す事は怪しい）を
今つけてるかって言われたら

以前にも紹介した
　「面積の測れない不思議な図形」や
　「バナッハ＝タルスキーのパラドックス」など

「数学的にパラドキシカル（に見える）な結果を含む
研究と言うのは、
まずほとんど選択公理が使わてる」んです。

数学界の問題児。
何かきな臭い、異常に見える事件が起こった時は確実に選択公理が使われてます。

うん、だからねー。
問題はそんな簡単じゃないんですよ。(´･ω･`)

選択公理は
過去に何度も「パラドックスか！？」と思われる事件を引き起こした
前科がある以上、
本当に、
本当に「無限回の選択を行う」行為と言うのは許されるべき行動なのか、
よくよく考えてみないといけないんですねー。（´д｀;

ちなみに前述の
　「面積の測れない不思議な図形」や
　「バナッハ＝タルスキーのパラドックス」など
の問題は数学的には無問題。パラドックスは起きてないとされています。

その理由は主に測度論の可測性によるもので、
面積について「可測性を満たす図形のみに面積を考える事は許される」として
集合を限定してるからです。

いわゆる紳士クラブ。

面積をこねくりまわしてパラドックスが起こる、もしくは起こらせるような
特殊な集合については「可測性を満たしていない」
として測度論の外に押し出し、中の秩序を守る事で「可測性を満たす」範囲内では
矛盾のない理論を組み立てて平和を守っているからです。

本当にヤバいのはこの後なんですねー
今みたのは氷山の一角。
問題はもっとデカい。

選択公理とは
　「『無限回の選択を行う』と言う行為は、本当に許されるのだろうか？」

レベルの話ではなく、実は

　「選択公理とは『無限回を超える回数の選択を行う』行為」
を許してしまう事だと気づく。

これまた以前にも解説しましたが、
無限にも種類と大きさのランクがあって
一番小さい無限が可算無限ω₀。実数の数と同じです。だから1、2、3・・・と数えてれば∞には到達はできなくとも、
だんだんと∞には近づいてゆくし、「任意の数以上」までは近づける。
ぎりぎり数えれる範囲。

ところが次の無限ω₁は非可算。
1、2、3のような数え方では永遠に到達不可能なサイズ。

ここで「選択＝1つの動作」説が出てくるわけです。
つまり「選択＝1つの動作」として解釈する限りはω₁回の選択と言うのは絶対に出来ない。
仮に0秒で1選択を終えたとしてもω₁回の選択は完了しきれない。

こうなってくると人間的に考える「選択」としては不可能な動作になってくる。

もっと、
ω₁サイズの集合を格納＆把握し、
　ガシャーンと1動作でω₁サイズの集合を出力する
「ω₁サイズ選択」とも言うべき別の動作と考えた方がいい。

人間と言うか数学の証明自体が、1行＋1行＋1行＋1行・・・の積み重ね。
可算な行為であるで・・・・
ここを逸脱して
非可算の領域まで扱える能力を持つって実はちょっとヤバいんじゃないかと気づいてくる・・（´д｀;

いや、と言うか
選択公理は
その気になれば到達不可能基数回数に対してだって選択を行ってしまいます。

・・・あああ。これはヤバい。(((( ；ﾟДﾟ)))ｶﾞｸｶﾞｸﾌﾞﾙﾌﾞﾙ

瞬間的にわかりますわ。
顔から血の気が引いてフリーズします。

問題が異次元レベルすぎて、YESなのかNOなのか予想がつけられないし、微塵もできる気がしない。

選ぶって事は、
集合の中の要素を全て一回通って、その中から選んでくるわけですからー。

人間は到達不可能基数に到達できません。（名前の通り）
その未知の対象、人間の能力を超える基数を相手に
選択公理は到達不可能基数回数でも選んでみせると豪語しておるわけで。

実は到達不可能基数を超えるサイズの理論もあって、「巨大基数」と呼ばれてますが
選択公理はそいつらさえも問題なしに巨大基数回数の選択を行う事ができる。

・・・・いや、この能力は本気でヤバいでしょ。^^A;
敵を限定しない、どんな奴が相手でもその中を全て通って選択してくる演算能力があるってのはあまりにも強力すぎる。

「俺はどんな奴にも勝てる」とか言っちゃったら
「自分より強いのか？　→　強くても弱くても引き分けでも矛盾」
みたいな形のパラドックスが起きる可能性がある。

だから「誰が相手でも」みたいに完全無条件にしちゃうのは危険だし、
その対象を自分に向かると矛盾が発生しやすい
典型的な激ヤバルート。

だから選択公理はヤヴァい。相手のサイズを限定しないってトンデモチート能力を与えてしまっている。

が！
その一方で。
選択の原理自体は自明で
選択行為に問題があるとは思えないし、
「横の対象が無条件に広すぎる」事を除けば
一般的には選択公理を採用する方が
数学的にリッチ、およびナチュラルな形になる。

と言うか逆に選択に条件をつけてしまうと
「今議論してる事は選択条件違反に接触していないか」常にチェックしなければおらず
今後の議論が大変面倒になる。

だから問題がないなら選択公理は有効としておいた方がいいのもまた事実。

本当に分からないので
「とりあえず、数学界全域に通達ぅー。選択公理、および選択公理に依存してる定理は使わない事。
　もし今後、選択公理に矛盾が見つかったら公理から取り下げる事になって研究が全部パーになるので非常に危険です。
　使う時は自己責任で。」と
って私でもサーキットブレイクかけてたでしょうねー。(^_^;

幸い選択公理が使われる範囲は狭く、
一般の数学を行ってる限りはまず呼ばれる事はありません。
禁止してもなんとかなりそうな状況だったので。

次回に大騒動の続き。

「数学コラム数学界に大論争を呼んだ選択公理2 （2015/01/22)」

さて、結論から述べますが
その後、ゲーデルの研究により
　「選択公理に（通常の環境下では）矛盾は含まれない、すなわち使って問題はない」
事がわかりました。

具体的にはゲーデルは「構成可能集合L」を考えました。

「構成可能」とは・・・
いわゆる「定義できる」の事です。

これまた以前にもした話ですが
数学と言うのは
　「数とは何か。数学V宇宙の脊髄を自然数が走る。第4章」で
した話ですが

数学と言うのは「空集合 = {}」から始まって、
空集合の上に選択を作って
S₀ ＝空集合 = {}
S₁ ＝ 2^S₀ = {}, {{}}
S₂ ＝ 2^S₁ = {}, {{}}, {{{}}}, {{},{{}},}
S₃ ＝ 2^S₂ = {}, {{}}, {{{}}}, {{},{{}}}, {{{{}}}}, {{},{{{}}}}, {{{}},{{{}}}}, {{},{{}},{{{}}}}
S₄ ・・・・・
のような各階層nに2ⁿのメンバーを持つピラミッド階層型に構築します。

数学的に考察可能な対象、
例えば「数字」、「二次元」、「面積」、「π」、などのなんらかの「値」的な性質を持つ
ありとあらゆる物体は
このピラミッドの中に出てきます。
（正確に言えば、同じ性質を持つサブ構造をWの中に発見できる）

このS_n全体を集めた物をWと呼びます。

（Vと呼ぶ場合もあります。
　通常はV＝Wとなるのでそれほど区別する必要もありませんが。

　厳密にはV＝全集合のクラス
　W＝well-founded（矛盾がないように、ピラミッド型によく構築された構造）。の意味合い。
　Vが性質的な要請で、Wがその要請を満たした具体的なモデルです。
　Vは矛盾排除のためwell-foundedな性質を要求する必要が必ずありますし、
　well-foundedな性質を持たせるとWができあがるので
　通常はV＝Wに勝手になっちゃいます。

　ただしときどきは後述のV＝Lのような別の世界観もある）

Wは数学の完全体。数学の学問としての全ての研究対象はこの中に詰まっています。

逆に言えば、Wに属さない構造を持った集合は矛盾を孕む可能性があるので
（例：ラッセルの集合。 R = {x:R∉x}）
数学としては研究の対象になりません。

少なくともいまの数学にある問題・難題・研究対象としての構造は全てWの中で表現できるので
W以外の構造を考察する意味はほとんどありません。
実質的に「W＝数学全体の考察対象」が
現代数学のデファクトスタンダードと言えます。

ただ・・・・実際はちょーっと違うんですねー^^;

と言うのも数学を扱うのは人間であり、
人間が書けるのは文字であり、
文字数には限界がある。

すなわちいくらWが数学の完全体と言っても
その中で「有限の長さの文章で記述可能な対象」の範囲でしか
人間には現実的に考察可能でありません。

例え宇宙が無限に広いと言っても、人間の目で観測できる範囲にしか
人間には知る術はなく、
手の届かない範囲は学術的に全くタッチできないんです。

座標を記録するにしたって必ずスペースの問題がある。
無限の座標を紙・ノート・PC・HDDに書くってのは不可能で、
必ず有限個に厳選しなければいけない。その範囲でしか我々は作業できない。

ゲーデルはそれを厳密に考察して
「構成可能集合L」を構築しました。

LはWのサブセットで、
Wの中から「人間が有限の文章で記述できる範囲」に絞った物と考える事ができます。

そしてLはWに比べると、相当シンプル化されています。

その理由としてはまあルベーグ積分的なアイディアに似ており
すなわち人間には文字が有限である以上
せいぜいω₀程度の複雑さを持った構造、もしくは方程式しか記述できないんですね。

それらω₀程度の複雑さを
いくら集めてもω₀程度の複雑さにしか
成り得ないし、
結局ω₀複雑さがLの上限。
人間に記述できる数学の上限になる。

と、Lおよび人間の限界を示したことです。

そしてLは選択公理をみたします。
その理由としてはLはω₀程度の複雑さしかないので。
ω₀複雑さから選択した結果はω₀複雑さの
中に留まる。問題をいま以上に難しくしないのでOK．

---------------

さて。
我々が本当に恐れていたのは選択公理の無差別性。
すなわち到達不可能基数や巨大基数に対しても
選択を行えてしまう強大無比なパワーだったのですが
それは杞憂に終わりました。

なぜなら人間に記述できる数学はLが上限。

Lの中だけで考えていればいいし、
どう頑張ってもL以上の考察は無理なので、

Lの範囲を超える到達不可能基数サイズや巨大基数サイズの集合に対して選択公理を適用すると言った状況は
通常の数学をやってる上ではまず永遠に
訪れないとわかったからです。
（やろうと思えばできます・・・しかし巨大基数用の追加公理が必要でこれはかなり異端になる）

ちなみに・・・はい。
到達不可能基数サイズを持つモデルの中には
選択公理の否定、すなわち選択公理からパラドックスを導くモデルもあります。
（コーエン1960年の論文）

もっともそのモデルと言うのはω₀より高い複雑さを持つ物体であり、
人間文字によっての具体的な記述は不可能。
具体例を誰も作れない以上
やはり考える必要はありません。（´д｀;
（人間には記述できないが、あると言うことは証明できる）

---------------

この「記述可能性」ってのは現代数学においては結構重要な問題でして、

これまた前に私がやったガロア理論と、5次元方程式の解法の不可能性のお話
や、
よくわかるカオスとフラクタル数学的解法の限界

などもこの一種なんですが。

つい400年ぐらい前までは数学界では「どんな問題でも解けるはず。解けないのは研究が足りないからだ！」って
超絶イケイケな風潮でしたが^^;
ここ100年ぐらいは数学の限界性、
　「・・・・いやちょっと待って。ひょっとして、無理。この問題は解けない・・・・んじゃないか・・・？」
がまこと活発に議論されてます。

NP問題だったり、カオス問題だったり、整数論問題だったり。
解けない物は解けない。恐らく解法が存在しないんじゃないだろうかってわかってきました。

それは例えば
　「一般5次元方程式の解は、√を使う方法だけじゃ記述できない」
と判明したように、
　「○○問題の解および証明は、人間の扱うL数学では記述できないのでは？」
ってのと同じで、人間がL数学とω₀複雑性に縛られてる以上は証明できる範囲に限界があるんです。（´д｀;

あ、ただしゲーデルの完全性定理があるので「正しい事柄＝必ず証明できる方法がある」ってのはわかるのですが。
依然としてその「正しい事柄」かどうかの判定が、人間のL数学でできるのか？
って問題になるわけでして。

恐らく、多くの整数論関係の問題なんかはNP問題的な性質、
すなわち「全ての数字のパターンを調べつくす」以外の方法はない性質を持ち、
そして「全ての数字を調べる」事は人間にはできないので
「有限の行数では証明（判定）に到達できない」と私は思ってます。(^_^A;

そうなると「有限の行数では証明を得られない」、証明不可能性を示す手順/システム/アルゴリズムが必要になったり。
いやそれすらもL数学には辿り着けないのかも。

いずれにせよ人間（数学）は非常に非力で、W全体のほんの僅か僅か僅かしか
知ることができないと言うのは
現代の集合論的見地からは妥当と言えるのではないでしょうか？

---------------

まとめると：
　・選択公理は完全無矛盾ではない。適用すると矛盾の発生するモデルもある。
　・が、そのモデルはL以上の複雑さを持っており、人間には記述不可能。
　・人間の記述できる数学、構築可能集合Lの中では選択公理は無矛盾
　・よって実質的には選択公理を「（通常の環境下では）矛盾を含まない」、
　　絶対的な真理、
　　公理として採用することには問題はない。

ってな事がその後の研究でわかり、
晴れて選択公理は無矛盾。常に真として成立する絶対的な真理。
集合論の公理の1つとして採用する至りとなったわけです。

ご拝聴ありがとうございました。